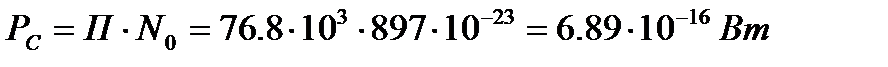Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
П.6 Первичный аналитический расчет требуемой вероятности ошибочного приема символа
Универсальным методом декодирования блочных кодов, который является оптимальным по критерию максимального правдоподобия, является декодирование по метрике Хемминга. В нашем техническом задании указанно, что при неоднозначном минимуме происходит пропуск сообщения. Для оценки вероятности ошибки декодера строго, нужно перебрать всевозможные разрешенные комбинации. Это значит, что для каждой разрешенной комбинации нужно перебрать всевозможные варианты и для каждого варианта проанализировать решение декодера. На практике для количественного анализа декодера используют гарантированный подход, который обеспечивает заведомо худшие показатели качества, чем те что есть на самом деле. Этот подход основан на том, что вместо ансамбля передаваемых кодовых слов рассматривают только 2 разрешенные комбинации на минимальном расстоянии Хемминга (Dmin) друг относительно друга. Из полученной матрицы кодовых слов мы видим, что Для того, чтобы определить какой кратности декодер обнаруживает ошибки нужно: Для того, чтобы узнать какой кратности наш декодер будет исправлять ошибки, нужно:
Следовательно, наш декодер будет обнаружить ошибки первой кратности, а исправлять ошибок не будет вообще. Примем, что данный канал является каналом без памяти, т.е. пакетных ошибок не будет. Тогда, согласно теории вероятности, вероятность ошибки i-ой кратности в блоке из n символов, находится по следующей формуле [3, стр. 179, формула (5.48)]:
Где:
Найдём вероятности правильного приёма сообщения:  Найдём вероятности ошибочного приёма сообщения: Найдём вероятности пропуска сообщения:
Из ТЗ известны вероятности ошибочного приема и пропуска сообщения. Графически найдем Рс:
Рис.12 Зависимость вероятности пропуска сообщения от вероятности ошибки в символе
Рис.13 Зависимость вероятности ошибочного приема сообщения от вероятности ошибки в символе
По рис. 12, 13 видим что вероятности ошибки в символе не совпадают. Выбираем минимальное значение. Следовательно, Рис.14 Зависимость вероятности ошибочного приема сообщения от вероятности ошибки в символе равной 0,0157
По рис.14 видно что вероятность ошибочного приема сообщения равна 0.00144
П.7 Структурная схема демодулятора. Первичный аналитический расчет требуемых энергетического отношения в символе, энергетического потенциала радиолинии, средней мощности сигнала на входе приемника.
Рис.15 Структурная схема демодулятора
Рассматриваемый канал является каналом с замираниями и качество приема характеризуется вероятностью ошибки, усредненной по всем возможным значениям амплитудных коэффициентов передачи
Для ФМ-2, при отсутствии замираний, вероятность битовой ошибки вычисляется по формуле:
где
Поскольку при наличии замираний энергетическое соотношение h2=h2(A) является случайной величиной, то в этих условиях качество приёма характеризуется вероятностью ошибки, усредненной по всем возможным значением амплитудных коэффициентов передачи: [3, стр. 244-245, формулы (7.28), (7.29)]
Тогда для релеевских замираний и двоичной системы сигналов с равными энергиями усреднение даёт вероятность ошибки при когерентном приёме:
Рис.16
Определим h2, согласно данному графику (pc = 0.00144). hср2=230.48.
Теперь, зная энергетическое отношение сигнал-шум, можем найти энергетический потенциал радиолинии:
Спектральная плотность аддитивного белого Гаусговского шума:
где Tш=650ºК шумовая температура антенны, k постоянная Больцмана.
Найдем минимальную мощность сигнала на входе приемника:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 379. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . Следовательно Мы имеем эквидистантный код.
. Следовательно Мы имеем эквидистантный код.
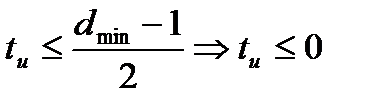

 - биноминальный коэффициент, pэ=pc – вероятность ошибки в символе.
- биноминальный коэффициент, pэ=pc – вероятность ошибки в символе.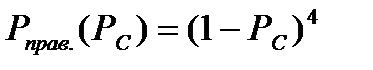




 7. При этом необходимо пересчитать вероятность ошибочного приема сообщения.
7. При этом необходимо пересчитать вероятность ошибочного приема сообщения.

 ,
, - интеграл вероятности;
- интеграл вероятности; - коэффициент взаимной корреляции.
- коэффициент взаимной корреляции.




 ,
,