
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Определениеоптимальной ГППЗ
Для решения задач методом линейного программирования в пакете прикладных программ WinQSB понадобится раздел – LinearandIntegerProgramming. В качестве критериев оптимальности будут использованы: 1) максимум выпуска в натуральном выражении; 2) максимум выпуска в стоимостном выражении; 3) максимум трудоемкости; 4) максимум прибыли; 5) максимум прибыли с учетом потерь от простоев оборудования; 6) многокритериальная задача; 7) максимум прибыли с ограничениями по спросу на выпускаемую продукцию.
1.Начнем с модели, целевой функцией которой является «Максимум выпуска в натуральном выражении с ограничением на спрос». Исходный план для нецелочисленной задачи представлен на рис. 3.1, его решение – на рис. 3.2. Аналогично для целочисленной задачи: решение – рис. 3.3.
Рис. 3.1. Исходный план для расчета оптимальной ГППЗ по критерию
Рис. 3.2. Результаты расчета оптимальной ГППЗ по критерию
Рис. 3.3. Результаты расчета оптимальной ГППЗ по критерию
Полученные решения позволяют не только получить оптимальный план решения задачи, но и проанализировать его и, возможно, улучшить в дальнейшем. Очевидно, что использование нецелочисленного решения предоставляет больше возможностей: в этом случае программа рассчитывает интервалы устойчивости и оптимальности полученного плана. Остановимся подробнее на рис. 3.2. Его верхняя часть демонстрирует оптимальное решение, в которое входят изделия 1, 2, 3, 4и 5. Как видно из графы «Reducedcost»: увеличение выпуска на одну единицу изделия 1 приведет к уменьшению значения целевой функции на 1,0653шт. и увеличение выпуска на одну единицу изделия 3 приведет к уменьшению значения целевой функции на 0,7957 шт.  Целевая функция будет ровняться 6252,975 штукам, однако, поскольку невозможно выпустить не целое изделие, все полученные значения будем округлять в меньшую сторону. Воспользовавшись стандартными правилами округления, велика вероятность выйти за рамки существующих производственных мощностей. Кроме вышеуказанных параметров, полученное решение позволяет проанализировать наши ресурсы. Например, можно с уверенностью утверждать, что дефицитного оборудования на предприятии нет. Однако, увеличение количества оборудования под номерами 5 и 6 приведет к увеличению выпуска. При этом последние два столбца демонстрируют границы устойчивости плана, т.е. при колебании эффективных фондов времени соответствующего оборудования в указанных границах структура плана будет оставаться прежней, но значение целевой функции будет увеличиваться. Также можно сказать обратно: первая, вторая и седьмая группы оборудования используются не значительно, следовательно, часть «лишнего» оборудования можно продать. Впрочем, послеоптимизационному анализу и улучшению выбранной модели будет посвящена следующая глава. Отметим также, что каждая из моделей имеет свои достоинства и недостатки. Преимуществом критерия является то, что он помогает определить максимальное количество выпущенных единиц. Недостаток заключается в том, что критерий никоим образом не связан с финансовой стороной производства – не предоставляет данные о получаемой выручке или прибыли, а также стоимости выпущенной продукции. Критерий «Максимум выпуска в натуральном выражении» целесообразно применять при выпуске однородной продукции.
2. Далее перейдем к следующей модели – «Максимум выпуска в стоимостном выражении с ограничением на спрос». Получаемое решение аналогично в каждом случае, поэтому не будем повторяться. При появлении дополнительных данных будут даны соответствующие пояснения. Исходный план нецелочисленной задачи представлен на рис. 3.4, его решение – на рис. 3.5.
Рис. 3.4. Исходный план для расчета оптимальной ГППЗ по критерию
Рис. 3.5. Результаты расчета оптимальной ГППЗ по критерию
Отметим еще раз, что целочисленное решение является более удобным в плане отсутствия нужды округлять значения. В то же время, он не демонстрирует границы оптимальности и устойчивости, из-за чего усложняется дальнейший анализ плана. В данной модели можно пояснить значения последних двух столбцов верхнего ряда. Они представляют нижние и верхние границы интервала оптимальности. Согласно их значениям, можно утверждать, что: · выпуск изделия 1 будет оставаться не выгодным, пока его цена не превысит 91250,96руб/шт. · выпуск изделия 3 будет оставаться не выгодным, пока его цена не превысит 54548,54руб/шт. · выпуск изделия 4 будет оставаться не выгодным, пока его цена не превысит 64187,91руб/шт. · выпуск изделия 5 будет оставаться не выгодным, пока его цена не превысит 73898,63 руб/шт. Преимущество данной модели заключается в том, что она позволяет определить такую производственную программу, когда оборот денежных средств будет максимальным, но при этом не учитываются затраты, связанные с простоем оборудования. Это, несомненно, является недостатком критерия. Возможно, такой критерий целесообразно применять, когда происходит «завершение» производства и необходимо из имеющихся ресурсов получить максимальную отдачу (увеличить коэффициент фондоотдачи). Тогда в оптимальный план попадут наименее трудоемкие и наиболее дорогие изделия.
3. Следующей моделью будет «Максимум трудоемкости с ограничением на спрос». Исходный план нецелочисленной задачи представлен на рис. 3.6, его решение – на рис. 3.7.
Рис. 3.6. Исходный план для расчета оптимальной ГППЗ по критерию
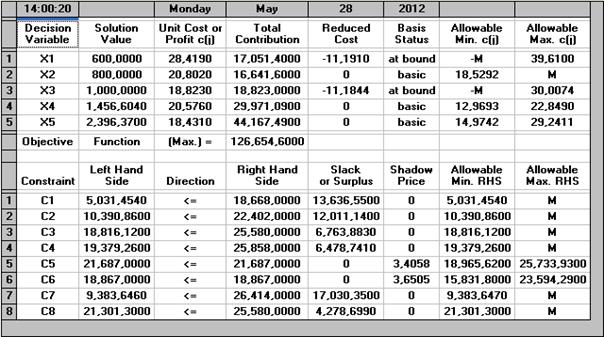
Рис. 3.7. Результаты расчета оптимальной ГППЗ по критерию
Настоящая модель направлена на минимизацию простоев оборудования, это ее основное достоинство. Отметим, что трудоемкость в данном случае определяется в часах. Однако, опять же, как и в первой модели при использовании такой целевой функции не учитываются денежные составляющие плана, т.е. выручка, прибыль и т.д. При данных условиях целесообразно производить изделия: первое в количестве 600 шт., второе в количестве 800 шт., третье в количестве 1000 шт., четвертое в количестве 1456,6 шт., пятое в количестве 2396,37 шт. суммарная трудоемкость при этом составляет 126654,6. Данный критерий используется, когда неизвестна цена, себестоимость, прибыль от изделия, а также, когда заготовки, находящиеся в производстве, требуют быстрой обработки. Для этого требуется постоянная, равномерная работа оборудования.
4. Далее рассмотрим модель «Максимум прибылис ограничением на спрос». В ней коэффициенты целевой функции ровняются величине прибыли, которую приносят соответствующие изделия. Исходный план нецелочисленной задачи представлен на рис. 3.8, его решение – на рис. 3.9. Аналогично для целочисленной задачи: решение – рис. 3.10. Рассматриваемый критерий позволяет сфокусироваться на получении максимальной прибыли от выпускаемой продукции. Однако, он также не учитывает потери от простоев оборудования.
Рис. 3.8. Исходный план для расчета оптимальной ГППЗ по критерию
Рис. 3.9. Результаты расчета оптимальной ГППЗ по критерию
Рис. 3.10. Результаты расчета оптимальной ГППЗ по критерию
Данный критерий наиболее важен и распространен, т.к. прибыль – один из важнейших показателей эффективности деятельности предприятия.
5. Следующим критерием будет «Максимум прибыли с учетом простоев оборудования». Именно этот критерий позволяет максимизировать получаемую прибыль, учитывая при этом минимизацию простоев оборудования, что является безусловным преимуществом модели. Исходный план нецелочисленной задачи представлен на рис. 3.11, его решение – на рис. 3.12.
Рис. 3.11. Исходный план для расчета оптимальной ГППЗ по критерию
Рис. 3.12. Результаты расчета оптимальной ГППЗ по критерию
В настоящей модели добавляются дополнительные переменные, равные соответствующим величинам простоев оборудования. Также отметим, что при решении целочисленной задачи соответствующие условия можно устанавливать лишь на переменные, которые отражают количество выпускаемых изделий. При данных условиях производятся все изделия. Изделие три и пять производятся в том же количестве. Первое изделие в количестве 600 шт., второе – 8000 шт., третье – 1493 шт., четвертое – 2167 шт., пятое – 800 шт. Прибыль составит 62 697 170. Рассматриваемый критерий целесообразно использовать при составлении бизнес-планов для определения прибыли с учетом убытков от простоев.
6. Далее рассмотрим модель по критерию максимум прибыли без ограничения на спрос. Данный критерий наиболее распространен, т.к. прибыль – один из важнейших показателей эффективности деятельности предприятия. Исходный план нецелочисленной задачи представлен на рис. 3.13, его решение – на рис. 3.14.
Рис. 4.12. Исходный план для расчета оптимальной ГППЗ по критерию
Рис. 4.14. Результаты расчета оптимальной ГППЗ по критерию
При данных условиях выпускается второе изделие в количестве 4286,69 шт. и третье изделие в количестве 2109,68 шт. Прибыль составит 85 728 100 рублей.
7. Рассмотрим многокритериальную модель с ограничениями на спрос. Вкачестве критериев будут использованы: · максимум объема выпуска в натуральном выражении:
C(x) = x1+x2+x3+x4+x5=>max;
· максимум прибыли:
C(x) = 12611x1+ 15402x2+ 9340x3+ 11713x4+7855x5=>max;
· максимум трудоемкости:
C(x) = 25,42x1+20,8x2+18,82x3+20,57x4+18,43x5=>max.
Целевая функция такой многокритериальной модели будет иметь вид:
где Используем метод свертки критериев для сведения критериев в одну модель. Величина Zφm,например, по прибыли, определяется по формуле:
По весовым коэффициентам должно соблюдаться условие:
После переведения коэффициентов в условные единицы целевые функции примут вид: · максимум объема выпуска в натуральном выражении:
C(x) = 0,2x1+0,2x2+0,2x3+0,2x4+0,2x5=>max;
· максимум прибыли:
C(x) =0,22x1+ 0,27x2+ 0,16x3+ 0,21x4+ 0,14x5=>max;
· максимум трудоемкости:
C(x) =0,24x1+0,20x2+0,18x3+0,20x4+0,18x5=>max.
Теперь ставим веса важности для критериев: · максимум объема выпуска в натуральном выражении – 10:
C(x) = 2x1+2x2+2x3+2x4+2x5=>max;
· максимум прибыли – 55:
C(x) =12,18x1+ 14,88x2+ 9,02x3+ 11,32x4+ 7,59x5=>max;
· максимум трудоемкости – 35:
C(x) =8,55x1+6,99x2+6,33x3+6,92x4+6,20x5=>max.
Складываем функции по столбцам и получаем конечную функцию:
C(x) = 22,73x1+23,88x2+17,35x3+20,24x4+15,79x5=>max.
Рис.2.14. Результаты расчета оптимальной ГППЗ по критерию «Многокритериальная модель с ограничением по спросу»
Рис.2.15. Результаты расчета оптимальной ГППЗ по критерию «Результат решения многокритериальной задачи с ограничением по спросу» (нецелочисленная задача)
Многокритериальная модель позволяет объединить сразу несколько показателей эффективности, рассмотреть задачу сразу с нескольких сторон. Может использоваться только когда известны и цена, и прибыль, и трудоемкость изделий. Таким образом, при данных условиях сумма коэффициентов составит 117 412,4 рубля.Производимое количество первого изделия составит 600 шт., второго – 800 шт., третьего – 1000 шт., четвертого – 1456 шт., пятого – 2396 шт. Результаты расчета ГППЗ по разным критериям заносятся в таблицу 3.1.
Таблица 3.1
Результаты расчета ГППЗ по разным критериям
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||













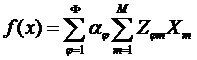 ,
, – индекс критерия оптимальности; Ф – число критериев оптимальности; αφ – весовой коэффициент φ-го критерия; Zφm– приведенный к нормированной шкале коэффициент φ-го критерия по m-му изделию.
– индекс критерия оптимальности; Ф – число критериев оптимальности; αφ – весовой коэффициент φ-го критерия; Zφm– приведенный к нормированной шкале коэффициент φ-го критерия по m-му изделию.

 .
.
