
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ВНУТРЕННЕЙ БАЛЛИСТИКИ ⇐ ПредыдущаяСтр 3 из 3 2.1. Основные сведения из термодинамики Как было сказано выше, выстрел представляет собой сложный термодинамический и газодинамический процесс очень быстрого превращения химической энергии пороха сначала в тепловую, а затем в механическую работу перемещенbz снаряда, откатных частей орудия и заряда. Орудие можно рассматривать как тепловую машину. Ниже приводятся основные сведения из термодинамики применительно к выстрелу. Энергией тела называется его способность совершать работу. Термодинамика – наука, занимающаяся изучением законов превращения энергии, при котором происходит изменение температуры участвующих в процессе тел, обмен тепла между ними и совершение механической работы. Превращение тепловой энергии в механическую в тепловой машине (двигателе) совершается при помощи промежуточного тела, которое называется рабочим телом. Большей частью рабочим телом служит газ, например, пороховые газы. Газ характеризуется величинами, которые носят название параметров состояния. К параметрам состояния относятся: давление, удельный объем, удельный вес и температура. Давление – р – сила, действующая по нормали со стороны газа на единицу площади поверхности оболочки. Согласно кинетической теории вещества давление газа р численно равно 2/3 кинетической энергии поступательного движения молекул, заключенных в единице объема. где m – масса газов, v скорость молекул газов. В артиллерийской технике давление газа измеряется в кг/см2 или кг/дм2.  Удельный объем – w - объем, занимаемый единицей веса вещества. где W – объем, ω – вес вещества Удельный вес – γ – вес единицы объема. Величина его обратна удельному объему. Иногда вместо удельного веса γ пользуются массовой плотностью газа, она равна где g – ускорение силы тяжести, равное 98,1 дм/сек2. Температура представляет собой степень нагретости тела и выражается в градусах или по стоградусной шкале Цельсия (t ºC) или по абсолютной шкале (Т К), связь между ними имеет вид Т К = 273 º + t ºC (2.5.) За рубежом используется шкала Фаренгейта (F). Перевод температуры по шкале Фаренгейта (Цельсия (t ºф) в температуру по шкале Цельсия (t ºС) осуществляется по формуле Термическое уравнение состояния газа – это фундаментальная связь между параметрами состояния газа. Оно имеет вид: F = (р, w, Т) = 0 или р = ƒ1 (w, Т), Т = ƒ2 (р1 w), w = ƒ3 (р1 Т) Как известно, в физике различают два вида газов: идеальные и реальные Идеальным называют газ, молекулы которого не имеют объема и лишены сил взаимодействия. Для него уравнение состояния имеет вид: р · w = R T (2.7.) Которое называется уравнением Клайперона и где R – газовая постоянная. Для произвольного объема уравнение (2.7.) имеет вид p W = ω R T (2.8.) Газовую постоянную R можно определить , зная удельный объем w, при атмосферном давлении и 0 ºС где pa = 103,3 кг/дм2 Для пороховых газов, имеющих w1 = 800 – 1000 дм3/кг
Газовая постоянная R представляет собой работу, совершаемую 1 кг данного газа, расширяющегося под постоянным давлением при нагревании на 1 ºС. Если в уравнении (2.8.) принять вес газа ω равным молекулярному весу – μ, уравнение примет вид: p ·Wμ = μ R T = Rμ · Т (2.9.) Где Wμ объем 1 моля газа Rμ = μ · R – универсальная газовая постоянная Согласно закона Авогадро объем молей всех идеальных газов Wμ при одинаковых температурах и давлениях одинаковы. При р = ра и Т = 273 К, Wμ = 22,4 г/дм3 = 22400 кг/дм3. Тогда Ввиду того, что Rμ = μ · R, значение R для данного газа можно получить, зная молекулярный вес газа. Практика показала, что связь между параметрами состояния реальных газов уклоняется от уравнения состояния идеальных газов. Имеется много различных формул для учета взаимодействия молекул и их собственного объема, например, уравнение Ван дер Ваальса: где: “а” и “в” – постоянные для данного газа; в – поправка, учитывающая собственный объем молекул. Во внутренней баллистики она носит название коволюма и обозначается буквой α. При высоких температурах газа, например, при выстреле, величина В таком случае уравнение состояния реального газа можно представить в виде: Газ, подчиняющийся этому состоянию носит название газ Дюпре. Смесь газов Пороховые газы представляют собой смесь различных газов (около ста), основными из которых являются: N2, H2, O2, CO, CO2, H2O, H, OH. Для определения параметров смеси необходимо знать ее состав, который может выражаться концентрацией весовой, объемной или молярной каждого газа в смеси. Весовой концентрацией данного газа в смеси (весовая доля) называют отношение веса этого газа к весу смеси. где: gi – весовая доля i-го газа; ωi – вес i-го газа в смеси; ω – вес смеси, причем Объемная концентрация представляет собой отношение нормального объема данного газа к объему смеси где: чi – объемная доля i-го газа; Wi – парциальный объем i-го газа (объем, который занимает газ при давлении и температуре смеси; W – объем смеси, причем Молярная концентрация есть отношение числа молей данного газа к объему числу молей смеси) где: Мi – число молей i-го газа смеси; М – общее число молей в смеси, причем Средний кажущийся молекулярный вес смеси μ определяется как:
Связь между gi, чi имеет вид
Газовая постоянная смеси определяется как где: μ – средний кажущийся молекулярный вес смеси; Ri – газовая постоянная i-го газа. Парциальное давление рi – давление, которое оказывал бы i-ый газ, занимая без других газов объем смеси при температуре смеси. рi = р чi где Удельный вес смеси γ определяется из выражения где γi – удельный вес i-го газа Термодинамические процессы Систему материальных тел, находящихся в механическом и тепловом взаимодействии друг с другом и окружающими телами, называют термодинамической системой. Механическое взаимодействие проявляется в совершении механической работы, тепловое взаимодействие – в переходе теплоты от одних тел к другим. Если система не может обменяться теплотой с окружающими телами, то ее наоборот называют теплоизолированной. Если система не взаимодействует с другими телами, она называется изолированной (замкнутой). Система, имеющая во всех своих частях одинаковые свойства, называется однородной. Система находится в равновесии, если параметры состояния ее не являются функциями времени. При изменении внешних условий, в которых находится термодинамическая система, состояние системы, также будет меняться и параметры ее будут функциями времени. Последовательность изменений состояния системы называют термодинамическим процессом. Процессы могут быть равновесными и неравновесными. Равновесный процесс, когда в каждый момент устанавливается термодинамическое равновесие (т.е. изменения идут медленно или сами изменения очень малы). Процессы бывают обратимыми и необратимыми. Циклом называют замкнутый процесс, когда система, проходя через ряд промежуточных состояний, возвращается в первоначальное состояние. Равновесные процессы можно изобразить графически в двухосной системе координат. На рис. 3 изображены изохорный, изобарный, изотермический и адиабатические процессы
A (p = const) В1
w1 w2 w3 w Рис. 3 Изохорный процесс (w = const) изображен на рис. 3 отрезком прямой АА1. Изобарный процесс (р = const) изображен на рис. 3 отрезком прямой АВ1. Изотермический процесс процесс (Т = const) – отрезком гиперболы и адиабатический процесс (р·wк = const) – отрезком кривой АВ3. Изохорный процесс – процесс, протекающий при неизменном объеме, т.е. при w = const. Связь между другими двумя параметрами состояния р и Т получается непосредственно из уравнения (2.7.) где Как видно, давление газа прямо пропорционально температуре. Изобарный процесс, процесс, протекающий при неизменном давлении р = const. Связь между другими двумя параметрами состояния w и Т получается непосредственно из уравнения (2.7.) где Как видно, объем газа прямо пропорционально температуре. Изотермический процесс, процесс, протекающий при неизменной температуре Т = const Связь между другими двумя параметрами состояния р и w получается непосредственно из уравнения (2.7.) Адиабатический процесс, процесс, протекающий без теплообмена с окружающей средой. Связь между параметрами состояния находится из двух уравнений: уравнения состояния (2.7.) и уравнения адиабаты (2.12.)
где к – показатель адиабаты Теплоемкость газа Кроме параметров состояния газа (р, w, и Т) большую роль в термодинамических процессах играет физическая величина, называемая теплоемкостью. Теплоемкость газа представляет собой количество тепла – q, сообщаемое единице веса газа в данном процессе при изменении его температуры на 1 ºС. Как видно из определения, характер процесса оказывает существенное влияние на величину теплоемкости. Теплоемкость – С измеряется в ккал/кг·град. Различают истинную и среднюю теплоемкость. Истинная теплоемкость где: q – количество тепла; t – температура газа в ºС, соответствует бесконечно малому изменению температуры газа в ходе конкретного термодинамического процесса. Теплоемкость газа существенно зависит от температуры. Для пороховых газов зависимостью теплоемкости от давления пренебрегают. В диапазоне температур 2000 – 3500 ºС. Теплоемкость можно принять изменяющуюся от температуры по линейному закону. С = а + вt º Где а и в – числовые коэффициенты, зависящие от физико-химических свойств газа и характера протекающего в нем термодинамического процесса. Средняя теплоемкость -
В термодинамических расчетах широко применяются теплоемкости изохорного (Сw) и изобарного (Ср) процессов, а также отношение этих теплоемкостей Коэффициент К называется показателем адиабаты. Для идеальных газов К является величиной, зависящей лишь от числа степеней свободы. По данным кинетической теории для одноатомных газов В баллистике чаще применяется разность между К и 1 и обозначается буквой θ
Величины К и θ являются функциями температуры. Значение Q убывает с увеличением температуры. Из физики известно, что μ Ср - μ Сw = А·Rμ= 2 Где μ С – молярная теплоемкость, ккал/кмоль·град Для смеси газов теплоемкость C определяется по формуле (2.14.) где: Сi – теплоемкость i-го компонента смеси; qi – весовая доля i-го компонента смеси. Внутренняя энергия газа Увеличение температуры газа приводит к увеличению ее внутренней энергии. Под внутренней энергией подразумевается сумма его внутренней кинетической энергии молекул и внутренней потенциальной энергии молекул. Внутренняя энергия газа обозначается в термодинамике буквой “u” для единицы веса (1 кг) газа и через “U” для произвольного количества газа и измеряется в тепловых единицах “u” в ккал/кг, “U” в ккал. Внутренняя энергия реального газа определяется значениями двух термодинамических параметров при использовании уравнения состояния внутреннюю энергию газа можно представить как функцию, зависящую от 2-х параметров из 3-х. u = f1 (T, w), u = f2 (T, p), u = f3 (p, w). Отсюда следует, что изменение внутренней энергии газа не зависит от характера процесса перехода его от одного состояния к другому и определяется начальным и конечным состоянием газа, т.е. является однозначной функцией его состояния. На рис. 4 представлены различные процессы перехода газа из начального состояния (точка 1) в конечное состояние (точка 2). Процессы обозначены кривыми “a”, “в” и “c”.
Идеальный газ не обладает силами взаимодействия молекул. Его внутренняя энергия состоит лишь из кинетической энергии молекул. Таким образом, для идеального газа его внутренняя энергия является только функцией температуры u = f (T). Пороховой газ при выстреле из баллистического орудия для расчета внутренней энергии рассматривается
в с
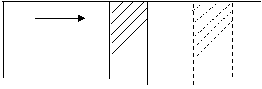
w1 w2 w Рис. 4 как идеальный, например, для изохорного процесса (w = const). Тепло, подведенное к газу q = Сw (t2º - t1º). Т.к. газ в этом процессе не совершает работу, все подведенное тепло идет на увеличение его внутренней энергии, т.е. Δu = q Δu = Сw (t2º - t1º) и ΔU = ω·Сw (t2º - t1º) = u2 – u1 Внешняя работа Определим внешнюю работу для случая, показанного на рис. 6. В цилиндре площадью сечение F помещен газ под давлением р. Цилиндр имеет дно и подвижный поршень, который удерживается противодавлением, а также давлением при нагревании газа весом 1 кг, помещенного между дном цилиндра и поршнем. Поршень будет (без трения) перемещаться вдоль цилиндра, испытывая противодавление р.
|
|||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 662. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
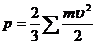 (2.1.)
(2.1.) , дм3/ кг (2.2.)
, дм3/ кг (2.2.) , кг/дм3 (2.3.)
, кг/дм3 (2.3.) (2.4.)
(2.4.) (2.6.)
(2.6.)



 (2.10.)
(2.10.) – поправка, учитывающая силы взаимодействия молекул;
– поправка, учитывающая силы взаимодействия молекул; (2.11.)
(2.11.)
 .
.
 .
.
 .
.


 - общее давление смеси.
- общее давление смеси.
 p
p




 p1
p1 p2 В
p2 В А1
А1 p3 В3
p3 В3

 - постоянная величина
- постоянная величина
 - постоянная величина
- постоянная величина или
или 

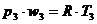


 - среднее значение в диапазоне температур t1º и t2º, которое определяется из соотношения
- среднее значение в диапазоне температур t1º и t2º, которое определяется из соотношения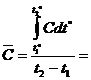
 (2.13.)
(2.13.)
 , для двухатомных
, для двухатомных  , для трехатомных
, для трехатомных  .
.




 (2.14.)
(2.14.)

 Р
Р 1
1


 Р1 a
Р1 a
 Р2 2
Р2 2




 p p
p p