
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Використання розвивального навчання на практиціПриведемо кілька прикладів використання розвивального навчання на практиці. При вивчені теми «Сума кутів трикутника» спочатку пропонуєм учням побудувати трикутник з кутами 80°, 50°, 70°. Вони швидко приступають до роботи з впевненістю, що такий трикутник побудувати можна. Але, коли їх спроби виявляються марними, учні замислюються, чому це так? В чому справа? В цей момент вони бувають як ніколи уважні, їх мислення активізується. При вивченні теми «Сума перших членів арифметичної прогресії» розповідаєм, що більше 200 років тому в одній із шкіл Німеччини на уроці математики учитель запропонував знайти суму перших 100 натуральних чисел. Всі почали додавати числа підряд, а один учень майже відразу дав правильну відповідь. Ім’я цього учня Карл Фрідріх Гаусс. Потім він став великим математиком. Як вдалося Гауссу так швидко підрахувати цю суму? Пропонуєм учням самостійно знайти розв’язання цієї задачі. Тема «Косинус кута». Спочатку введемо поняття прилеглого катета. Потім даєм завдання: накреслити прямокутний трикутник. Один із кутів позначте через α, виділіть прилеглий катет одним кольором, гіпотенузу – іншим. Знайдіть відношення цього катета до гіпотенузи. Продовжте катет і гіпотенузу і знову знайдіть відношення катета до гіпотенузи. Одержали те ж число. Деякі учні отримують однакові числа. Чому, маючи різні трикутники, довжини сторін різні, а відношення отримали однакові? Що це за магічне число? Від чого воно залежить. Даєм означення цього числа. Вивчаючи довжину кола, можна запропонувати задачу. Уявіть, що ви пройшли земну кулю по екватору. На скільки при цьому верхівка голови пройшла більш довший шлях, ніж кінчик вашої ноги? Як простіше розв’язати цю задачу? Такі задачі викликають інтерес до математики, розвивають мислення.  Проблемні ситуації можуть бути створені, якщо запропонувати учням задачу із недостатніми даними або зайвими даними, завдання-пастки. Знайдіть помилки: 1. -5,62+3,2= -2,6 2. (2ав-1)-2 = 4а-2в-2 3. х+1+ Головною вимогою цього методу є така організація навчання, при якій в учнів виникає активна мислительна діяльність, яка приводить до самостійного розв’язання задачі. Одним із важливих принципів розвивального навчання є оптимальний розвиток різних видів мислительності, розвиток математичних здібностей. У школі велику роль відіграє розвиток мислення, засобом якого є наочність, зорове сприйняття. На кожному уроці використовуєм наочність – формули, запис на дошці, малюнки і схеми, плакати і таблиці. Потрібно, щоб учень дивився на запропонований предмет і бачив те, що закладено в ньому. На дошці записано складний алгебраїчний вираз. Завдання – спростити його. Учні швидко беруться за ручки. Їх потрібно зупинити. Треба спочатку уважно розглянути вираз, подумати які знання, правила, формули треба використати для перетворення виразу. Наприклад. Розв’язати рівняння: 4х+3•22х-1+( 1. Це показникове рівняння. 2. У рівняння входять показникові функції з основами 4, 2, 3. Треба записати всі функції з однією основою 2. 4. Порівняємо показники. Помічаємо, що треба використати формулу аm+n,аm-n. 5. Всі доданки мають вигляд К*22х. Одержимо рівняння а*22х=5. Приклади таких завдань: 1. Розставте знаки множення у виразі: 2. Знайти однакові елементи і замінити їх буквою а:
3. Продовжити ряд:
Важливо складати план роботи. Учень повинен визначити деякі дії. Спочатку таке обговорення виконуємо вголос. Розв’язуючи такі завдання розвивається мислення (зорове,наочне). Пропонуючи учням різні схеми, таблиці, графіки, треба розфарбувати їх різними кольорами. Прикладами таких завдань може бути: читання графіка, побудова графіка функції, маючи певні властивості, пропонуєм набір графіків і набір формул. Враховуючи індивідуальні можливості учнів у процесах мислення, сприймання, запам’ятовування, проблему розвивального навчання не можна розвивати без диференційованого навчання. Клас можна поділити на три групи, перед якими ставим різні завдання. Одні учні повинні досягти рівня обов’язкових результатів навчання, інші повинні добиватися більш високих результатів. Склад груп можна змінювати, будь-який учень може перейти з однієї групи в іншу. Учні, які люблять математику, добре працюють на уроках, утворюють першу групу. Цим учням потрібні різноманітні і складні завдання. Друга група – середня. Це діти старанні, мають деякі математичні здібності, але працюють повільно. Для цих дітей важливо повірити в себе і навчитися розв’язувати складні завдання. Третя група – учні, які не люблять математику, не вміють працювати самостійно. Диференційований підхід здійснюєм на певних етапах уроку. На етапах введення нового поняття працюєм з усім класом. Після того як на дошці розв’язано декілька завдань, учні можуть працювати в групах: перша і друга групи розв’язують завдання самостійно, а учні третьої групи продовжують працювати під керівництвом вчителя. Потім учні третьої групи самостійно працюють над розв’язанням нескладних завдань, а учні першої і другої групи разом з учителем розв’язують завдання підвищеної складності. Самостійну роботу організовуєм по варіантах різної складності. В кожен варіант включаю завдання розвивального характеру, розв’язання яких вимагає нестандартного мислення. Наприклад: 1. Не виконуючи обчислення визначте, яким числом, додатнім чи від’ємним є значення виразу 3,2*1,6 -3,6. 2. Порівняйте з нулем числа k і в, якщо відомо, що на графіку функції у=kх+в немає жодної точки, у якій обидві координати додатні. 3. Відомо, що при деяких значеннях а і в значення виразу а – в=3.Чому дорівнює значення виразу а) 5а-5в; б)12в-12а в)(а-в)2 г)(в-а)2. 4. Розкладіть на множники многочлен а2-4ав-3а2в-6ав2+4в2. Різнорівневі завдання полегшують організацію занять у класі. У результаті подолання труднощів підвищувалась пізнавальна активність учнів. Для ефективної організації роботи на уроці можна впроваджувати групову роботу. В цьому випадку до кожної групи входять як сильніші учні, так і слабші. У цьому випадку поєднується фронтальна, колективна і індивідуальна робота. Такі групи виконують однакові завдання. Наприклад. Розв’язати систему рівнянь відомими вам способами. Кожен учень одержує індивідуальне завдання: один учень розв’язує систему графічно, другий – способом підстановки, третій – способом додавання. Після індивідуальної роботи кожного, учні приступають до групової: порівнюють відповіді, перевіряють правильність розв’язання, допомагають учням, які не справляються із з завданням. Проведення уроків, враховуючи індивідуальні особливості кожного учня, вимагає від учителя серйозної підготовки, накопичення великої кількості різноманітних завдань.
Після пояснення нового матеріалу починаєм роботу по індивідуальних картках з завданнями різної складності. Учні розрізняють їх за кольором. Учень сам обирає завдання, розв’язує його у зошиті. При цьому учень може користуватись зошитом, підручником, консультуватись з іншими учнями та вчителем. Всі роботи перевіряєм. Оцінка не повинна стати гальмуванням розвитку пізнавальної діяльності. Вона повинна бути стимулом його діяльності і творчої активності. Потрібно намагатись навчити учня слухати не тільки вчителя , а й своїх товаришів. Психологи всього світу довели, що забороняючи дітям спілкуватися під час уроку ми робимо кожного з них безпомічним, незахищеним, несамостійним, а тому більш залежним від учителя. Деякі учні бояться виходити до дошки. Таких не варто викликати поодинці. Нехай візьмуть з собою товаришів. Несмілива дитина не злякається і зрозуміє, що це зовсім не страшно. Такі діти відповідають на запитання лише після того, як порадяться з товаришами. Можна також практикувати на уроках «пастки» - завдання, які не мають розв’язків. Показуюм, щоб не потрапити до пастки не можна діяти, наслідуючи когось, а необхідно працювати самому. На уроках вчитель і учень працюють разом. Розв’язавши завдання, не запитуєм: « правильно?», а ставим запитання: «хто здогадався як думав товариш? Доведи. Поясни.» Вчитель помиляється учні виправляють. «Поясніть, чому я помилилася, що я не зрозуміла?». На таких уроках формується вміння запитувати і відповідати.
Висновок Щоб навчити дитину потрібні роки. Чому діти не хочуть вчитися? Причин багато. Традиційні програми, за якими ми працюємо не навчають дітей, а відучують дитину бути допитливими, висловлювати та відстоювати свою думку. Методика розвивального навчання дає змогу підтримувати і поглиблювати ті якості, на яких базується вміння навчатися. За розвивального навчання учитель бачить у дитині перш за все розумну істоту і розвиває її можливості. Таким чином, використання особисто орієнтованого навчання на уроках математики та у позаурочній роботі впродовж кількох років дає високі і стабільні результати: · дозволяє учням реально оцінювати свої можливості; · підвищується інтерес до предмету; · між вчителем і учнями встановлюються партнерські відносини; · знижується психологічна напругу учнів на уроках; · підвищується якість знань; · учні активніше працюють на уроках; · зникає страх перед перевіркою знань.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 243. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
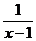 =
=  =х+2
=х+2 )3-2х=5
)3-2х=5
 (х-у)
(х-у) .
.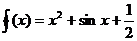 ;
; ;
; 

 .
.