
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Геометрические характеристики сеченийСтр 1 из 2Следующая ⇒ ОГЛАВЛЕНИЕ ВВЕДЕНИЕ.. Ошибка! Закладка не определена. 1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ.. 1 1.1. Геометрические характеристики сечений. 2 1.2. Классификация стержней. 3 1.3. Классификация сил. 4 1.4. Уравнения равновесия. 6 1.5. Напряжения. 7 1.6. Интегральные характеристики напряжений 1.7. Метод определения внутренних усилий. 9 1.8. Закон Гука при растяжении. 12 1.9. Закон Гука при сдвиге. 14 1.10. Гипотеза плоских сечений. 15 2. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ РАСТЯЖЕНИЯ, КРУЧЕНИЯ И ИЗГИБА ПРЯМЫХ СТЕРЖНЕЙ С УЧЁТОМ ТЕМПЕРАТУРНЫХ ЭФФЕКТОВ (МАЛЫЕ ПЕРЕМЕЩЕНИЯ) 17 2.1. Статические (динамические) уравнения. 17 2.2. Геометрические уравнения. 23 2.3. Физические уравнения. 29 2.4. Полная система дифференциальных уравнений 3. УСЛОВИЯ ПРОЧНОСТИ И ЖЁСТКОСТИ.. 31 3.1. Критерий прочности Губера–Мизеса. 32 3.2. Формулировка критерия прочности для частных случаев напряжённого состояния стержня 35 4. ЕДИНОЕ ПРЕДСТАВЛЕНИЕ РАСПРЕДЕЛЁННОЙ НАГРУЗКИ 4.1. Обобщённые функции Дирака и Хевисайда. 40 4.2. Табличные интегралы и их практическое применение. 47 4.3. Формулировка силовых граничных условий. 48 5. ТИПОВЫЕ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ.. 49 5.1. Расчёт балки на изгиб. 49 5.2. Расчёт ступенчатых стержней на растяжение. 51 5.3. Расчёт разрезной балки на изгиб. 53 КОНТРОЛЬНЫЕ ВОПРОСЫ... Ошибка! Закладка не определена. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.. Ошибка! Закладка не определена.
Основные понятия и определения  Сопротивление материалов – это наука об инженерных методах расчета элементов конструкций и машин на прочность, жесткость и устойчивость. Одним из основных разделов сопротивления материалов является техническая теория стержней. Уточним суть некоторых общих понятий. Деформация – изменение размеров и формы материальных тел под действием внешних нагрузок. Упругость – свойство материальных тел восстанавливать первоначальную форму и размеры после снятия нагрузки. Пластичность – свойство материальных тел не восстанавливать первоначальную форму и размеры после снятия нагрузки. Прочность – способность конструкций и деталей машин выдерживать рабочие нагрузки без разрушения и пластических деформаций. Жесткость – способность конструкций и деталей машин выдерживать рабочие нагрузки без значительных упругих деформаций, которые могут нарушить их нормальную работу. Устойчивость – способность конструкции и её элементов сохранять определенную начальную форму упругого равновесия под нагрузкой. Материальная однородность: материал, из которого изготовлено тело, проявляет одинаковые свойства во всех точках. изотропность: материал, из которого изготовлено тело, проявляет одинаковые свойства во всех направлениях.
Геометрические характеристики сечений Пусть имеется некоторая плоская фигура (сечение тела), связанная с декартовой системой координат
Рис. 1.1. Центр тяжести плоской фигуры По определению центром тяжести плоской фигуры называется геометрическая точка с координатами
где
Величины (1.2) называются статическими моментами фигуры относительно оси Ось, проходящая через центр тяжести сечения, называется центральной осью. Очевидно, если начало координат Осевым моментом инерции плоской фигуры называется интеграл произведения площади элементарной площадки на квадрат её расстояния от рассматриваемой оси. Так, моменты инерции плоской фигуры (рис. 1.1) относительно осей
Полярным моментом инерции плоской фигуры относительно данной точки (полюса
Поскольку
Центробежным моментом инерции плоской фигуры называется интеграл произведения площади элементарной площадки на её расстояния от координатных осей
Величины осевых моментов инерции Оси, относительно которых центробежный момент инерции равен нулю, называются главными осями инерции. Главные оси, проходящие через цент тяжести плоской фигуры, называются главными центральными осями.
Классификация стержней В сопротивлении материалов под стержнями подразумеваются тела довольно разнообразной и вместе с тем специфической формы. Представим себе некоторую линию, вдоль которой движется плоская фигура так, что её центр тяжести находится на этой линии, а плоскость фигуры нормальна к ней (рис. 1.2). Если размеры фигуры
Рис. 1.2. Прямой брус (стержень) постоянного сечения
Если поперечное сечение при движении вдоль оси не изменяется, то тогда имеет место стержень постоянного сечения; в противном случае – стержень переменного сечения. Если ось стержня – прямая линия, то это прямой стержень. Если ось стержня – кривая линия, то его называют кривымстержнем. Если поперечное сечение при движении вдоль оси вращается вокруг касательной к оси, то стержень называют естественно-закрученным. Примером прямого естественно-закрученного стержня постоянного сечения является рабочая часть сверла. Используются также и другие названия. В частности, стержень, работающий на изгиб, обычно называют балкой, а стержень, передающий вращательное движение, – валом.
Классификация сил В механике понятие силы является первичным (неопределяемым) понятием. В качестве пояснения (но не определения) можно указать, что под силой понимается мера механического взаимодействия материальных тел, которое вызывает их деформацию и ускоренное движение. По характеру взаимодействия все силы можно разделить на объёмные (массовые) и поверхностные силы. Массовые (объёмные) силы обусловлены взаимодействием материальных тел на расстоянии, они приложены к каждой точке тела (распределены по всему его объёму). К массовым силам относятся силы гравитационного и электромагнитного взаимодействия. Обычно из чисто формальных соображений к ним добавляют силы инерции (для сил инерции невозможно указать конкретный материальный источник). Поверхностные силы приложены к участкам поверхности и являются результатом взаимодействия материальных тел при непосредственном контакте. В зависимости от соотношения площади приложения нагрузки и общей площади поверхности рассматриваемого тела, поверхностные силы подразделяются насосредоточенные и распределённые. К первым относятся нагрузки, площадь приложения которых несоизмеримо меньше площади поверхности тела. Таковыми являются, например, сила нормального давления По отношению к выбранному материальному телу (элементу конструкции) все действующие силы подразделяются на внешние и внутренние силы. Под внешними силами (нагрузками) понимаются силы взаимодействия данного материального тела со всеми другими окружающими его телами. Под внутренними силами понимаются силы взаимодействия между частями данного тела.
Рис. 1.3. Подкрановая балка и её расчётная схема
Понятно, что деление сил (нагрузок) на внешние и внутренние силы является условным. Одна и та же сила может быть и внутренней и внешней, всё зависит от выбора объекта исследования. К примеру, на бетонный блок, лежащий на подкрановой балке, действует вес
Рис. 1.4. Типовые связи (опоры) и их реакции
Как правило, равновесие конструкций, состоящих из одного или нескольких элементов, обеспечивается наложением тех или иных связей. Наиболее распространёнными связями являются гладкая или шероховатаяповерхность (опора), шарнирно-неподвижная опора (шарнир), шарнирно-подвижная опора (опора на катках), невесомый стержень, заделка (рис. 1.4). Для конструкции в целом, состоящей из стержней 1–3, реакции врезанных шарниров В соответствии с этим внешние силы, действующие на выделенное тело, подразделяются на активные (заданные) силы и реактивные силы. Реактивные силы возникают в связях, наложенных на тело, их величина определяется действующими на тело активными силами.
Уравнения равновесия В теоретической механике доказывается, что для равновесия свободного абсолютно твёрдого тела, находящегося под действием некоторой системы внешних сил
где
– момент силы В проекции на координатные оси два векторных уравнения (1.7) дают шесть скалярных уравнений равновесия:
С их помощью можно найти не более шести неизвестных величин, в большинстве случаев – это реакции внешних (для данного тела) связей.
Рис. 1.5. Равновесие материального тела
Применительно к деформируемому твёрдому телу уравнения (1.7), (1.8) являются необходимыми, но не достаточными условиями равновесия. В качестве наглядного примера можно указать на ножницы (рис. 1.6). Для их равновесия нужно наложить дополнительные связи, например, заварить врезанный шарнир
Рис. 1.6. Равновесие деформируемого тела Напряжения Рассечём тело некоторой плоскостью и отбросим одну из частей тела (рис. 1.7, а). Для плоскости сечения выберем то направление орта нормали
называется вектором напряжения на данной площадке. В общем случае вектор напряжения зависит не только от положения точки Вектор напряжения можно разложить на две составляющие, одна из которых направлена по нормали
Рис. 1.7. Вектор напряжения (а), нормальное и касательное напряжения (б) Так как при сечении тела была взята внешняя нормаль
1.6. Интегральные характеристики напряжений Рассмотрим произвольное плоское сечение нагруженного стержня (рис. 1.8). Выберем декартову систему координат На каждой элементарной площадке Рис. 1.8. К определению интегральных характеристик напряжений
Компоненты главного вектора
Каждая из компонент (1.9) имеет характерное название:
|
|||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 173. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и имеющая площадь
и имеющая площадь 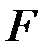 (рис. 1.1).
(рис. 1.1). ,
,  , (1.1)
, (1.1) ,
,  . (1.2)
. (1.2)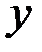 и
и  соответственно. Такое название дано по аналогии с понятием момента силы относительно оси, если только в качестве силы иметь в виду площадь фигуры.
соответственно. Такое название дано по аналогии с понятием момента силы относительно оси, если только в качестве силы иметь в виду площадь фигуры. совпадает с центром тяжести сечения
совпадает с центром тяжести сечения  , то обе координатные оси будут центральными осями. Относительно них
, то обе координатные оси будут центральными осями. Относительно них  , ибо в этом случае
, ибо в этом случае  .
. и
и  соответственно равны
соответственно равны ,
,  . (1.3)
. (1.3) ) называется интеграл произведения площади элементарной площадки на квадрат её расстояния до полюса (рис. 1.1):
) называется интеграл произведения площади элементарной площадки на квадрат её расстояния до полюса (рис. 1.1): . (1.4)
. (1.4) , из (1.3) находим
, из (1.3) находим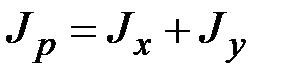 . (1.5)
. (1.5) ,
,  (рис. 1.1):
(рис. 1.1): . (1.6)
. (1.6) ,
,  и полярного момента инерции
и полярного момента инерции  плоской фигуры всегда положительны. Напротив, центробежный момент инерции
плоской фигуры всегда положительны. Напротив, центробежный момент инерции  в зависимости от положения осей может быть либо положительным, либо отрицательным, либо равным нулю.
в зависимости от положения осей может быть либо положительным, либо отрицательным, либо равным нулю. ,
,  существенно меньше длины линии
существенно меньше длины линии  , то описанное указанным образом тело называется стержнем (или брусом); соответственно отмеченная плоская фигура называется поперечным сечением стержня, а отмеченная линия – осью стержня.
, то описанное указанным образом тело называется стержнем (или брусом); соответственно отмеченная плоская фигура называется поперечным сечением стержня, а отмеченная линия – осью стержня.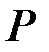 и сила трения
и сила трения  между колесом тележки и подкрановой балки, а также силы взаимодействия балки с опорами
между колесом тележки и подкрановой балки, а также силы взаимодействия балки с опорами  ,
,  ,
,  , Z2(рис. 1.3, а). При составлении расчётной схемы суммарный эффект от действия этих нагрузок представляется в виде сосредоточенных сил и моментов (рис. 1.3, б). Если же площадь приложения нагрузки сопоставима с площадью поверхности тела, то такая нагрузка рассматривается как распределённая. Таковыми являются, например, силы давления, вызываемые весом бетонного блока
, Z2(рис. 1.3, а). При составлении расчётной схемы суммарный эффект от действия этих нагрузок представляется в виде сосредоточенных сил и моментов (рис. 1.3, б). Если же площадь приложения нагрузки сопоставима с площадью поверхности тела, то такая нагрузка рассматривается как распределённая. Таковыми являются, например, силы давления, вызываемые весом бетонного блока  (рис. 1.3, в). Действие этого блока на подкрановую балку заменяется погонной нагрузкой
(рис. 1.3, в). Действие этого блока на подкрановую балку заменяется погонной нагрузкой  , которая характеризует величину силы давления, приходящейся на единицу длины (рис. 1.3, а).
, которая характеризует величину силы давления, приходящейся на единицу длины (рис. 1.3, а). и распредёленная нагрузка
и распредёленная нагрузка  , направленная в противоположную сторону (рис. 1.3, в). По отношению к блоку обе эти нагрузки внешние. Однако для механической системы, включающей в себя блок и балку, погонная нагрузка является внутренней распределённой силой.
, направленная в противоположную сторону (рис. 1.3, в). По отношению к блоку обе эти нагрузки внешние. Однако для механической системы, включающей в себя блок и балку, погонная нагрузка является внутренней распределённой силой. ,
,  (на рис. 1.4 не показаны) являются внутренними силами. Но для каждого из стрежней в отдельности эти реакции будут внешними силами, как и реакции остальных связей (опор).
(на рис. 1.4 не показаны) являются внутренними силами. Но для каждого из стрежней в отдельности эти реакции будут внешними силами, как и реакции остальных связей (опор). , необходимо и достаточно выполнения двух векторных уравнений равновесия (рис. 1.5):
, необходимо и достаточно выполнения двух векторных уравнений равновесия (рис. 1.5): ,
,  , (1.7)
, (1.7)
 относительно точки
относительно точки  ,
,  – радиус-вектор приложения указанной силы с началом в точке (центре)
– радиус-вектор приложения указанной силы с началом в точке (центре)  . Если тело несвободно (из-за наложенных на него связей), то, пользуясь принципом освобождаемости от связей, последние надо мысленно отбросить и заменить их действие силами реакций, которые будут внешними силами по отношению к освобождённому указанным образом телу.
. Если тело несвободно (из-за наложенных на него связей), то, пользуясь принципом освобождаемости от связей, последние надо мысленно отбросить и заменить их действие силами реакций, которые будут внешними силами по отношению к освобождённому указанным образом телу. (1.8)
(1.8) .
. , которое является внешним для оставшейся части тела. Поскольку до рассечения между обеими частями имело место взаимодействие, то в соответствии с принципом освобождаемости от связей действие отброшенной части на оставшуюся часть следует заменить поверхностными силами, распределёнными по всему сечению. На бесконечно малую площадку
, которое является внешним для оставшейся части тела. Поскольку до рассечения между обеими частями имело место взаимодействие, то в соответствии с принципом освобождаемости от связей действие отброшенной части на оставшуюся часть следует заменить поверхностными силами, распределёнными по всему сечению. На бесконечно малую площадку  сечения с центром в точке
сечения с центром в точке  будет действовать бесконечно малая сила
будет действовать бесконечно малая сила  . Величина
. Величина
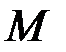 , но и от ориентации площадки, т.е. от направления орта нормали
, но и от ориентации площадки, т.е. от направления орта нормали  , что и отражено в обозначении
, что и отражено в обозначении  в виде нижнего индекса.
в виде нижнего индекса. , а другая – перпендикулярно к ней (рис. 1.7, б). Составляющая
, а другая – перпендикулярно к ней (рис. 1.7, б). Составляющая  , направленная по нормали
, направленная по нормали  , называется нормальным напряжением на площадке
, называется нормальным напряжением на площадке  . Составляющая
. Составляющая  , лежащая в плоскости площадки
, лежащая в плоскости площадки  , называется касательным напряжением на этой площадке. Очевидно, что
, называется касательным напряжением на этой площадке. Очевидно, что .
. , растягивающие нормальные напряжения являются положительными, а сжимающие напряжения – отрицательными. Можно было бы поступить и наоборот, выбрав при сечении тела внутреннюю нормаль. Тогда сжимающие напряжения были бы положительными, а растягивающие напряжения – отрицательными. Оба случая используются на практике.
, растягивающие нормальные напряжения являются положительными, а сжимающие напряжения – отрицательными. Можно было бы поступить и наоборот, выбрав при сечении тела внутреннюю нормаль. Тогда сжимающие напряжения были бы положительными, а растягивающие напряжения – отрицательными. Оба случая используются на практике. ,
,  ,
,  с началом в центре тяжести сечения
с началом в центре тяжести сечения  . Ось
. Ось  направим по нормали сечения
направим по нормали сечения  .
. сечения будет действовать вектор напряжения
сечения будет действовать вектор напряжения  (нормаль
(нормаль  направлена по оси
направлена по оси  ). Полное напряжение
). Полное напряжение  разложим на нормальное напряжение
разложим на нормальное напряжение  и касательное напряжение
и касательное напряжение 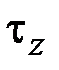 . В плоскости площадки
. В плоскости площадки  направление касательного напряжения
направление касательного напряжения  в общем случае произвольно. Чтобы обойти эту неопределённость, разложим полное касательное напряжение
в общем случае произвольно. Чтобы обойти эту неопределённость, разложим полное касательное напряжение  по координатным осям
по координатным осям 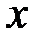 и
и  , обозначив составляющие через
, обозначив составляющие через  ,
,  соответственно (рис. 1.8).
соответственно (рис. 1.8). и главного момента
и главного момента  распределённых по сечению напряжений относительно центра тяжести плоского сечения
распределённых по сечению напряжений относительно центра тяжести плоского сечения  называются или интегральными характеристикаминапряжений, или внутренними силовыми факторами, или внутренними усилиями в сечении. Они равны
называются или интегральными характеристикаминапряжений, или внутренними силовыми факторами, или внутренними усилиями в сечении. Они равны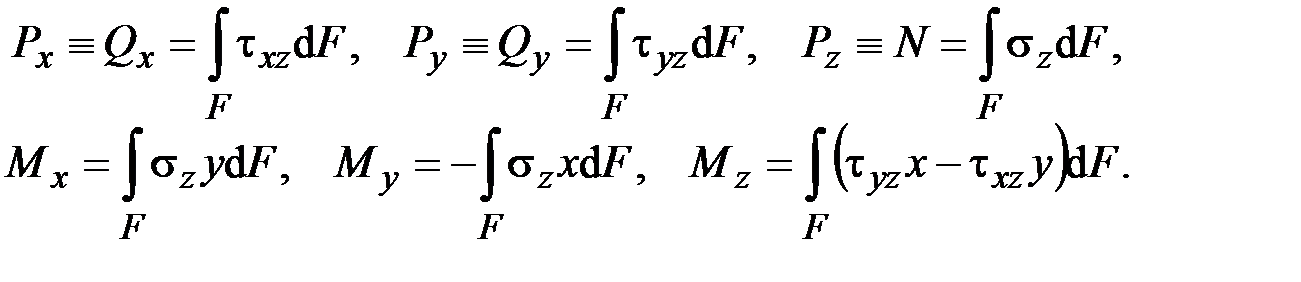 (1.9)
(1.9) – продольная (нормальная) сила;
– продольная (нормальная) сила; 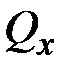 ,
,  – поперечные (перерезывающие) силы;
– поперечные (перерезывающие) силы;  ,
,  – изгибающие моменты;
– изгибающие моменты;  – крутящий момент.
– крутящий момент.