
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Необходимый и достаточный признаки возрастания и убывания функции.Стр 1 из 3Следующая ⇒ Правила дифференцирования. Таблица производных. Производная сложной и неявно заданной функции. Логарифмическая производная. (Правила и таблицу скинула тебе в картинках) 1. Продифференцировать обе части уравнения по независимой переменной 2. Решить полученное уравнение относительно производной Если y=f(u), где u=u(x), то есть y — сложная функция, то производная сложной функции находится по следующему правилу: y’=f'(u)·u'(x), то есть производную внешней функции f надо умножить на производную внутренней функции u. Дифференциал функции, его геометрический смысл. Применение дифференциала к приближенным вычислениям. Дифференциалом функции называется линейная относительно
Геометрический смысл. Дифференциал функции в точке Для приближенного вычисления значения функции применяется следующая формула:
Основные теоремы дифференциального исчисления. Теорема Ферма. (О равенстве нулю производной) Пусть функция – она дифференцируема на интервале – достигает наибольшего или наименьшего значения в точке  Тогда производная в этой точке равна нулю, то есть
Теорема Ролля. (О нуле производной функции, принимающей на концах отрезка равные значения) Пусть функция – непрерывна на отрезке – дифференцируема на интервале – на концах отрезка Тогда на интервале
Теорема Лагранжа. (О конечных приращениях) Пусть функция –непрерывна на отрезке –дифференцируема на интервале Тогда на интервале
Теорема Ролля есть частный случай теоремы Лагранжа, когда
Теорема Коши. (Об отношении конечных приращений двух функций) Если функции непрерывны на отрезке дифференцируемы на интервале производная тогда на этом интервале найдется по крайней мере одна точка
Если производная функции равна нулю на некотором промежутке, то функция является постоянной на этом промежутке. Ема Если две функции имеют равные производные на некотором промежутке, то они на этом промежутке отличаются друг от друга на некоторое слагаемое. Необходимый и достаточный признаки возрастания и убывания функции. Необходимое условие возрастания функции. Если функция y = f(х) дифференцируема и возрастает на интервале [а, b], то f '(х) > 0 для всех х из этого интервала.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 217. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и функция
и функция  связаны уравнением вида
связаны уравнением вида 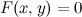 , которое не разрешено относительно
, которое не разрешено относительно 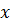 , предполагая, что
, предполагая, что  – это дифференцируемая по
– это дифференцируемая по 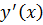 .
.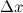 часть приращения функции. Она обозначается как
часть приращения функции. Она обозначается как 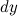 или
или 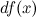 . Таким образом:
. Таким образом: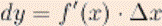
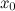 равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента
равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента 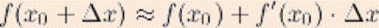
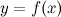 удовлетворяет следующим условиям:
удовлетворяет следующим условиям: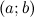 ;
;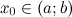 .
.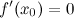 .
.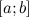 ;
;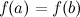 .
.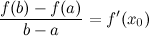 .
.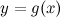 :
: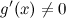 на интервале
на интервале  .
.