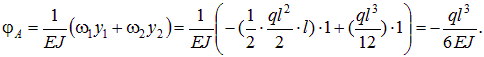Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Правило А.К. Верещагина «перемножения эпюр» ⇐ ПредыдущаяСтр 2 из 2 В 1924 г. студент Московского института инженеров транспорта Андрей Константинович Верещагин (1896–1959), ставший впоследствии инженером-полковником, заметил, что, если для стержня с постоянной жесткостью в формуле Мора одна из функций, стоящих в числителе, является линейной, вычисление интеграла можно упростить и вместо функциональных зависимостей MF (х) и Для случая
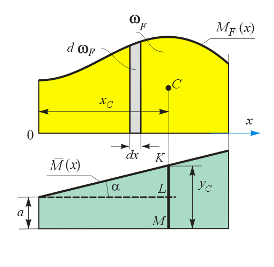
Покажем, как вычисление интеграла в формуле (9.3) сводится к использованию геометрических параметров соответствующих эпюр. На рис. 9.4 показана грузовая эпюра моментов МF от внешних нагрузок, предполагаемая произвольной,и единичная эпюра
Рис. 9.4. К выводу правила Верещагина А.К.
Уравнение для линейной эпюры запишем в виде:
Интеграл, входящий в (9.3), будет равен:
Первый интеграл, стоящий в правой части равенства, является площадью эпюры МF, которую обозначим wF. Учитывая, что 
где хС – расстояние от оси у до центра тяжести площади wF. В итоге приходим к равенству
Из рис. 9.4 нетрудно установить, что сумма, стоящая в скобках, равна
где: уС – ордината единичной эпюры, находящаяся под центром тяжести грузовой эпюры. Таким образом, для интеграла Мора получим окончательное выражение, называемое способом или правилом А.К. Верещагина:
Правило Верещагина. Интеграл от произведения грузовой и единичной эпюр равен площади грузовой эпюры, умноженной на ординату единичной эпюры под центром тяжести грузовой эпюры.
В случае, когда грузовая эпюра также линейная, в формуле (9.4) можно брать площадь любой из двух эпюр (грузовой или единичной). Произведение wF и уС следует брать с учетом знака. Оно может быть положительное или отрицательное. Для балок, где знаки на эпюрах моментов ставят (вверху «минус», снизу «плюс»), вычисление знака этого произведения не представляет трудности. В рамах принято знак момента не ставить, а эпюры строить со стороны растянутого волокна. Считают, что если эпюра МF и ордината эпюры Для балки, состоящей из нескольких участков, и для рам следует вычислять интегралы Мора по каждому из участков конструкции. Во многих случаях площадь грузовой эпюры, и особенно ее центр тяжести, найти затруднительно, поэтому рассмотрим способы разбиения сложных эпюр на простейшие. Ограничиваясь рассмотрением грузовых эпюр МF, имеющих вид квадратной параболы, приведем способ разбиения сложных эпюр на более простые, указав площади и положения центров тяжести отдельных частей. На рис. 9.5 показан способ разбиения «равнозначной» трапеции, у которой основания имеют одинаковый знак (рис. 9.5, а), «разнозначной» трапеции (рис. 9.5, б) и квадратной параболы (рис. 9.5, в).
Рис. 9.5. Способы разбиения эпюр
Буквами Для определения площади параболы можно проинтегрировать функцию M(x) для балки на двух опорах, загруженной равномерно распределенной нагрузкой q. На расстоянии х от левой опоры для этой балки:
где: f = ql2/8 – максимальное значение изгибающего момента посередине балки (эту величину часто называют «стрелкой параболы»), l – длина участка. Центр тяжести лежит посредине параболы. При разбиении сложных эпюр на более простые формула (9.4) будет иметь вид:
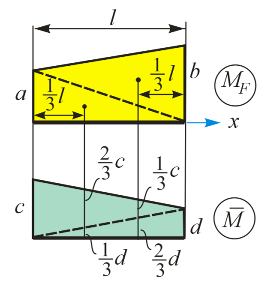
где: В случае, когда обе эпюры (грузовая и единичная) имеют вид трапеций (рис. 9.6), для вычисления интеграла от произведения этих эпюр существует формула «перемножения трапеций», вывод которой приведен ниже.
Рис. 9.6. К формуле «перемножения трапеций»
Значения a, b, c, и d в формуле (9.7) следует брать с учетом знака (выше – ниже оси). Надо разделить длину участка на шесть, а затем перемножить дважды левые ординаты, дважды правые ординаты и, далее, перемножить друг на друга ординаты, расположенные «крест на крест». Пример 9.2.Вычислим, используя правило Верещагина А.К. прогиб и угол поворота на левом конце балки, рассмотренной в примере 9.1. На рис. 9.7 показаны грузовая эпюра Грузовая эпюра разбита на треугольник, площадь которого равна Для удобства рассуждений стрелками показано положение частей грузовой эпюры относительно оси (сверху, снизу).
Рис. 9.7. К примеру 9.2
Ординаты единичных эпюр - для эпюры
- для эпюры
Подставляя полученные значения
Знак «плюс» при перемножении площади на соответствующую ординату получают при условии, что грузовая эпюра и ордината единичной эпюры находятся с одной стороны от базовой линии, а знак «минус» – когда грузовая эпюра и ордината единичной эпюры находятся по разные стороны от базовой линии. Знак окончательного результата «перемножения» эпюр имеет следующее значение. Положительный результат свидетельствует о том, что перемещение происходит по направлению единичного воздействия, а отрицательный – против. Так, например, знак «минус» в результате дляφА указывает на то, что направление угла поворота сечения балки в т. А противоположно направлению единичного момента, приложенного к балке. Метод Мора удобен при вычислении перемещений в рамах, поскольку позволяет вычислять не только вертикальные перемещения и углы поворота, но и горизонтальные перемещения.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 2748. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 использовать эпюры соответствующих моментов. Поэтому способ, полученный А.К. Верещагиным для вычисления интеграла от произведения двух функций, называют способом «перемножения эпюр». Слова «перемножение эпюр», поставлены в заголовке в кавычки, поскольку правило относится не к вычислению произведения эпюр, входящих в формулу Мора, а к интегралу от этого произведения. В случае стержневой системы, состоящей из прямолинейных стержней, единичная эпюра
использовать эпюры соответствующих моментов. Поэтому способ, полученный А.К. Верещагиным для вычисления интеграла от произведения двух функций, называют способом «перемножения эпюр». Слова «перемножение эпюр», поставлены в заголовке в кавычки, поскольку правило относится не к вычислению произведения эпюр, входящих в формулу Мора, а к интегралу от этого произведения. В случае стержневой системы, состоящей из прямолинейных стержней, единичная эпюра  преобразуем формулу (9.2) к виду:
преобразуем формулу (9.2) к виду:


 второй интеграл, равный
второй интеграл, равный  представляет собой статический момент площади wF относительно оси у, который равен:
представляет собой статический момент площади wF относительно оси у, который равен:

 ,
, .
.
 лежат с одной стороны от оси, то их произведение будет положительным, в противоположном случае – отрицательным.
лежат с одной стороны от оси, то их произведение будет положительным, в противоположном случае – отрицательным.
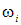 обозначены площади отдельных частей эпюры. На первый взгляд, трапецию логично разбить на прямоугольник и треугольник, но на самом деле удобнее представить трапецию как сумму двух треугольников, что позволяет ввести единообразие в использование правила А.К. Верещагина. На рис. 9.5, а треугольники ABD и A1B1D1 отличаются по форме, но их можно считать эквивалентными, поскольку, эти треугольники, имеющие одинаковое основание (b) и высоту (l), имеют равную площадь (
обозначены площади отдельных частей эпюры. На первый взгляд, трапецию логично разбить на прямоугольник и треугольник, но на самом деле удобнее представить трапецию как сумму двух треугольников, что позволяет ввести единообразие в использование правила А.К. Верещагина. На рис. 9.5, а треугольники ABD и A1B1D1 отличаются по форме, но их можно считать эквивалентными, поскольку, эти треугольники, имеющие одинаковое основание (b) и высоту (l), имеют равную площадь (  bl/2), и их центры тяжести находятся на одинаковом расстоянии (l/3) от основания. Показанная на рис. 9.5, б разнозначная трапеция разбивается на два треугольника, один из которых расположен выше базовой линии, а другой ниже. Если к балке приложена равномерно распределенная нагрузка q, то на соответствующем участке эпюра моментов представляется квадратной параболой (рис. 9.5, в). В этом случае суммарная эпюра разбивается на трапецию, которая рассмотрена выше, и «чистую» квадратную параболу (значения которой на концах участка равны нулю).
bl/2), и их центры тяжести находятся на одинаковом расстоянии (l/3) от основания. Показанная на рис. 9.5, б разнозначная трапеция разбивается на два треугольника, один из которых расположен выше базовой линии, а другой ниже. Если к балке приложена равномерно распределенная нагрузка q, то на соответствующем участке эпюра моментов представляется квадратной параболой (рис. 9.5, в). В этом случае суммарная эпюра разбивается на трапецию, которая рассмотрена выше, и «чистую» квадратную параболу (значения которой на концах участка равны нулю).
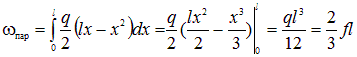

 .
.


 , а также две единичные эпюры:
, а также две единичные эпюры:  (от вертикальной единичной силы
(от вертикальной единичной силы  в т. A) и
в т. A) и  (от единичного момента в т. А).
(от единичного момента в т. А).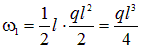 и «чистую» квадратную параболу площадью
и «чистую» квадратную параболу площадью 

 под центрами тяжести треугольника и параболы будут равны:
под центрами тяжести треугольника и параболы будут равны:
 ;
;
 .
.