
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Формула Мора для определения перемещений в плоских стержневых системахСтр 1 из 2Следующая ⇒ Понятие о перемещениях в плоских стержневых системах Перемещения в балках. Вычисление перемещений необходимо для расчетов балок на жесткость. Расчет на жесткость относится к второй группе предельных состояний. При изгибе балок рассматривают два вида перемещений – линейные и угловые. Линейные перемещения оси балки – это вертикальные перемещения, которые называются прогибами. В соответствии с введенными ранее обозначениями для перемещений будем обозначать прогибы буквой v. На рис. 9.1 пунктиром показана ось балки в деформированном состоянии, которая называется изогнутой осью балки. Уравнение изогнутой оси балки можно описать некоторой функцией
Рис. 9.1. Перемещения в балке
Правило знаков для v. Прогибы балки считаются положительными, если происходят в сторону положительного направления оси у, т.е. вниз. В сопротивлении материалов рассматриваются малые перемещения. В строительных конструкциях максимальные прогибы лежат в пределах 1/200-1/1000 длины балки. В балках возникают также и горизонтальные перемещения и, обусловленные, например, сближением концов балки. Эти перемещения намного меньше перемещений Пренебрегая горизонтальными смещениями центров тяжести сечений, будем полагать, что центр тяжести сечения перемещается строго вертикально, при этом сечение поворачивается на угол  Правило знаков для j.Углы поворота сечений балки считаются положительными, если происходят в направлении хода часовой стрелки. Перемещения в плоских стержневых системах. В плоских стержневых системах обычно находят три перемещения – два линейных и одно угловое. Линейные перемещения обозначают Δ с соответствующими индексами, а угловое – буквой
Рис. 9.2. Перемещения в раме
Формула Мора для определения перемещений в плоских стержневых системах Формулой, имеющей огромное практическое значение для расчета конструкций на жесткость, является формула Мора (9.1), названная по имени немецкого механика и инженера Отто Христиана Мора (1835–1918).жесткость).
Иногда формулу (9.1) называют формулой Максвелла – Мора, а стоящий справа интеграл – интегралом Мора. Замечание. В формуле (9.1) учитываются только те слагаемые, которые соответствуют конкретной задаче. При растяжении (сжатии) стержней отличными от нуля будут только продольные силы N, и остается только первое слагаемое (такой подход используется при вычислении перемещений в фермах при узловой нагрузке). Обычно, при расчете плоских стержневых систем, работающих, в основном, на изгиб (плоские рамы), пренебрегают членами с продольной и поперечной силами, что дает небольшую погрешность результатов (несколько процентов), а в формуле Мора оставляют только второе слагаемое. Таким образом, для плоских рам формула Мора запишется в виде:
Здесь: DKF – обобщенное перемещение некоторой точки К от действия внешних нагрузок (подчеркнуто вторым индексом F);
Так, для вычисления линейного перемещения какой-либо точки нужно приложить в этой точке единичную силу Единичная сила Пример 9.1.Рассмотрим балку, показанную на рис. 9.3. Изгибающий момент в балке от действия равномерно распределенной нагрузки описывается функцией
Рис. 9.3. К примеру 9.1.
Для определения вертикального перемещения т. А приложим в этой точкеединичную силу Функция единичного момента имеет вид Подставляя выражения для обоих моментов в формулу (9.1), получим:
Для определения угла поворота в той же точке приложим единичный момент
|
||||||||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 1029. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
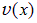 .
.
 и, как правило, не рассматриваются. Существует отдельная задача изгиба гибких стержней (гибких нитей), в которых перемещения могут быть значительными, но в данном курсе эта задача не приводится.
и, как правило, не рассматриваются. Существует отдельная задача изгиба гибких стержней (гибких нитей), в которых перемещения могут быть значительными, но в данном курсе эта задача не приводится.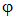 . Эти углы поворота и называются угловыми перемещениями. Так же, как и прогибы, значения
. Эти углы поворота и называются угловыми перемещениями. Так же, как и прогибы, значения  Следует отметить, что наличие поперечных сил приводит к искривлению сечений, однако с некоторым приближением можно считать, что и при поперечном изгибе справедлива гипотеза плоских сечений. Отсюда следует, что угол поворота сечения равен углу поворота касательной к изогнутой оси балки.
Следует отметить, что наличие поперечных сил приводит к искривлению сечений, однако с некоторым приближением можно считать, что и при поперечном изгибе справедлива гипотеза плоских сечений. Отсюда следует, что угол поворота сечения равен углу поворота касательной к изогнутой оси балки.

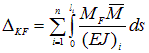
 – грузовая эпюра моментов (функция), полученная от внешних нагрузок;
– грузовая эпюра моментов (функция), полученная от внешних нагрузок; – единичная эпюра моментов (функция), полученная от действия единичной обобщенной силы.
– единичная эпюра моментов (функция), полученная от действия единичной обобщенной силы. и написать функцию (или построить эпюру)
и написать функцию (или построить эпюру)  от этой силы, после чего использовать формулу. Для вычисления угла поворота
от этой силы, после чего использовать формулу. Для вычисления угла поворота  и также найти функцию (построить эпюру)
и также найти функцию (построить эпюру)  являются безразмернымивеличинами, поэтому единичная эпюра
являются безразмернымивеличинами, поэтому единичная эпюра 


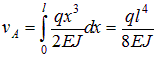 .
. направленный по часовой стрелке, предполагая, что угол поворота будет положительным. В этом случае
направленный по часовой стрелке, предполагая, что угол поворота будет положительным. В этом случае  Из формулы (9.1) находим
Из формулы (9.1) находим