
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Перевірка чисел на взаємну простоту (розширений алгоритм Евкліда). Теореми Міллера-Рабіната Ферма.
Нехайn - велике непарне число, і ми хочемовизначитичи єn простим. Теорема (Ферма). Якщоn - просте число, то згідно малої теореми Ферма для будь-якого такого b, що НОД (b, n) =1, Якщоn - не просте число, то (1) теж може виконуватись (хоча це малоймовірно). Визначення. Якщоn - непарнескладене число, b - ціле число, НОД (n, b) =1, і (1) виконується, то n називається псевдопростим числом за основою b. Іншими словами, "псевдопросте" число - це число n, яке "претендує" бути простим, проходячи тест (1). Приклад 1. число n = 91 - псевдопросте за основоюb = 3, так як Сильно псевдопросте число. Розглянем тепер ще один вид критеріїв простоти, що у певному сенсі навіть краще тесту Соловея - Штрассе, заснованого на взначенні псевдо простати по Ейлеру. Це тест Міллера-Рабіна, заснований на понятті "сильно псевдо простати". Припустим, що n –велике непарне натуральне число і  Визначення. Нехай n - непарнескладене число і n-1=2st, t -непарне. Нехай 1) 2) існує таке r,
то n називають сильно псевдопростим за основою b. Тест Міллера-Рабіна. Припустимо, що ми хочемо визначити, є велике натуральне число n простим чи складним. Уявімо n-1 у вигляді Зламування криптограм RSА. RSA - криптографічна система відкритого ключа, що забезпечує такі механізми захисту як шифрування і цифровий підпис (автентифікація - встановлення автентичності). Криптосистема RSA розроблена в 1977 році і названа на честь її розробників Ronald Rivest, Adi Shamir і Leonard Adleman. Алгоритм RSA працює наступним чином: беруться два досить великих простих числа p і q та обчислюється їх добуток n = p * q; n називається модулем. Потім вибирається число e, що задовольняє умові 1 <e <(p - 1) * (q - 1) і не має спільних дільників окрім 1 (взаємно просте) з числом (p - 1) * (q - 1). Потім обчислюється число d таким чином, що (e * d - 1) ділиться на (p - 1) * (q - 1). • e - відкритий (public) показник • d - приватний (private) показник. • (n; e) - відкритий (public) ключ • (n; d). - Приватний (private) ключ. Дільники (фактори) p і q можна або знищити або зберегти разом з приватним (private) ключем. Якби існували ефективні методи розкладання на співмножники (факторингу), то, розклавши n на співмножники (фактори) p і q, можна було б отримати приватний (private) ключ d. Таким чином надійність криптосистеми RSA заснована на важко вирішуваній - практично не вирішуваній - завдання розкладання n на співмножники (тобто на неможливості факторингу n) так як в даний час ефективного способу пошуку співмножників не існує. Припустимо, Аліса хоче послати Бобу повідомлення M. Аліса створює зашифрований текст З, зводячи повідомлення M в ступінь e і множачи на модуль n: C = M**e* (mod n), де e та n - відкритий (public) ключ Боба. Потім Аліса посилає С (зашифрований текст) Бобу. Щоб розшифрувати отриманий текст, Боб зводить отриманий зашифрований текст C в ступінь d і примножує на модуль n: M = c**d*(mod n); залежність між e і d гарантує, що Боб вирахує M вірно. Так як тільки Боб знає d, то лише він має можливість розшифрувати отримане повідомлення. Існує кілька способів злому RSA. Найбільш ефективна атака - знайти секретний ключ, відповідний необхідного відкритому ключу. Це дозволить нападаючому читати всі повідомлення, зашифровані відкритим ключем, і підробляти підпис. Таку атаку можна провести, знайшовши головні співмножники (фактори) загального модуля n - p і q. На підставі p, q і e (загальний показник) нападаючий може легко обчислити приватний показник d. Основна складність в пошуку головних співмножників (факторинг) n. Безпека RSA залежить від розкладання на співмножники (факторингу), що є важким завданням, що не має ефективних способів вирішення. Фактично, завдання відновлення секретного ключа еквівалентна задачі розкладання на множники (факторингу) модуля: можна використовувати d для пошуку співмножників n, і навпаки, можна використовувати n для пошуку d. Треба відзначити, що удосконалення обчислювального обладнання саме по собі не зменшить стійкість криптосистеми RSA, якщо ключі будуть мати достатню довжину. Фактично ж вдосконалення обладнання збільшує стійкість криптосистеми. Інший спосіб зламати RSA полягає в тому, щоб знайти метод обчислення кореня ступеня e з mod n. Оскільки С = Me mod n, то коренем ступеня e з mod n є повідомлення M. Обчисливши корінь, можна розкрити зашифровані повідомлення й підробляти підписи, навіть не знаючи приватний ключ. Така атака не еквівалентна факторингу, але в даний час невідомі методи, які дозволяють зламати RSA таким чином. Однак в особливих випадках, коли на основі одного і того ж показника відносно невеликий величини шифрується досить багато пов'язаних повідомлень, є можливість розкрити повідомлення. Згадані атаки - єдині способи розшифрувати всі повідомлення, зашифровані даними ключем RSA. Існують і інші типи атак, що дозволяють, однак, розшифрувати лише одне повідомлення і не дозволяють нападнику розкрити інші повідомлення, зашифровані тим же ключем. Також вивчалася можливість розшифрування частини зашифрованого повідомлення. Найпростіше напад на окреме повідомлення - атака по передбачуваному відкритому тексту. Нападник, маючи зашифрований текст, передбачає, що повідомлення містить якийсь певний текст, потім шифрує передбачуваний текст відкритим ключем одержувача і порівнює отриманий текст з наявним зашифрованим текстом. Таку атаку можна запобігти, додавши в кінець повідомлення кілька випадкових бітів. Інша атака на єдине повідомлення застосовується в тому випадку, якщо відправник посилає одне і те ж повідомлення M трьом кореспондентам, кожен з яких використовує загальний показник e = 3. Знаючи це, нападаючий може перехопити ці повідомлення і розшифрувати повідомлення M. Таку атаку можна запобігти, вводячи перед кожним шифруванням у повідомлення кілька випадкових бітів. Також існують кілька атак по зашифрованому тексту (або атаки окремих повідомлень з метою підробки підпису), при яких нападаючий створює деякий зашифрований текст і отримує відповідний відкритий текст, наприклад, змушуючи обманним шляхом зареєстрованого користувача розшифрувати підроблене повідомлення. Зрозуміло, існують і атаки, націлені не на криптосистему безпосередньо, а на вразливі місця всієї системи комунікацій в цілому. Такі атаки не можуть розглядатися як злом RSA, так як говорять не про слабкість алгоритму RSA, а скоріше про уразливість конкретної реалізації. Наприклад, нападаючий може заволодіти секретним ключем, якщо той зберігається без належної обережності. Необхідно підкреслити, що для повного захисту недостатньо захистити виконання алгоритму RSA і прийняти заходи математичної безпеки, тобто використовувати ключ достатньої довжини, так як на практиці найбільший успіх мають атаки на незахищені етапи управління ключами системи RSA. Дискретне логарифмування. Стійкість широко розповсюджених у даний час схем ЕЦП (електронний цифровий підпис) заснована на складності рішення приватної завдання дискретного логарифмування в простому полі GF (p). Завдання це формулюється наступним чином: • задані прості числа p, q і натуральне число g <p порядку q, тобто gqº 1 (modp); • знаючи значення y = gx (mod p), необхідно знайти x ÎZ. В даний час найбільш швидким алгоритмом рішення загальної задачі дискретного логарифмування (при довільному виборі g) є алгоритм узагальненого решета числового поля, обчислювальна складність якого оцінюється як O(exp((c+O(1))(ln (p))1/3(ln (ln (p)))2/3 операцій в полі GF(p), де c» (64/9)1/3. Методами рішення приватної завдання дискретного логарифмування є також r-метод и l-метод Полларда і деякі близькі методи, що вимагають для її вирішення виконання порядку Öpq/4 операцій множення в полі GF (p). (1.2) «При 1024-бітовому p і 256-бітовому q ми отримуємо приблизно 1.3E +26 для методу решета числового поля і 3.0E +38 для r- і l- методів Полларда». Національні стандарти DigitalSignatureStandard (прийнятий NIST в 1991 р. з наступними змінами в 1993, 1996 р.), російський стандарт цифрового підпису ГОСТ Р 34.10-94 реалізовують ЕЦП в простому полі. Прогрес в галузі вирішення задачі дискретного логарифмування привів до того, що стала можлива реальна компрометація схем ЕЦП, заснованих на складності обчислень у мультиплікативної групи поля, з боку порушника, який володіє досить невисокими обчислювальними і фінансовими ресурсами. Тому на рубежі XX і XXI століття в багатьох країнах світу стали використовуватися схеми формування ЕЦП, засновані на складності розв'язання задачі дискретного логарифмування в групі точок еліптичної кривої. Це завдання формулюється наступним чином: • задана еліптична крива E над полем GF (p), де p - просте число; • обрана точка G, що має простий порядок q в групі точок кривої E; • знаючи точку kG необхідно відновити натуральне число k. Алгоритми створення і перевірки ЕЦП, що базуються на математичному апараті еліптичних кривих, є стійкішими в порівнянні зі схемами, що базуються на складнощі вирішення задачі дискретного логарифмування в простому полі. В даний час найбільш швидкими алгоритмами розв'язання задачі дискретного логарифмування в групі точок еліптичної кривої при правильному виборі параметрів вважаються r- метод і l- метод Полларда і близькі їм методи. Їх складність оцінюється формулою (1.2) і, таким чином, числом близько 1038 операцій додавання точок кривої. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 675. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


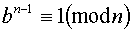 . (1)
. (1)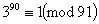 . Однак, 91 не є псевдопростим числом за основою 2, так як
. Однак, 91 не є псевдопростим числом за основою 2, так як 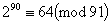 . Якщо б ми ще не знали, що 91 складене число, то
. Якщо б ми ще не знали, що 91 складене число, то 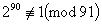 співвідношення довело б нам це.
співвідношення довело б нам це.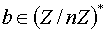 . Нехай, далі, n - псевдопросте за основою b, тобто
. Нехай, далі, n - псевдопросте за основою b, тобто 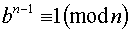 . Ідея критерію сильної псевдо простати така. Нехай
. Ідея критерію сильної псевдо простати така. Нехай 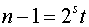 , t - непарне. Якщо послідовно обчислювати
, t - непарне. Якщо послідовно обчислювати 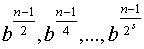 , то при простому n першим елементом, відмінним від 1, повинен бути елемент 1, так як при простому n єдиним рішеннямпорівняння
, то при простому n першим елементом, відмінним від 1, повинен бути елемент 1, так як при простому n єдиним рішеннямпорівняння 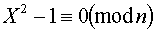 є +1 і-1. практично дії виконуються "у зворотномупорядку". Вважаємо
є +1 і-1. практично дії виконуються "у зворотномупорядку". Вважаємо 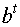 по модулю n. Якщо
по модулю n. Якщо 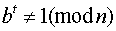 , зводимо в квадрат по модулю n, отримуємо
, зводимо в квадрат по модулю n, отримуємо 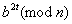 , потімзновузводимо в квадрат і т.д. до тих пір, поки не отримаємо 1:
, потімзновузводимо в квадрат і т.д. до тих пір, поки не отримаємо 1: 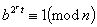 . Тоді, якщо n - просте, попереднім числом має бути - 1, в іншому випадку миотримуємо доказ того, що n складене.
. Тоді, якщо n - просте, попереднім числом має бути - 1, в іншому випадку миотримуємо доказ того, що n складене.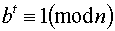 ;
;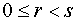 , що
, що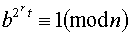 (2)
(2) , t непарне, і виберемовипадкове ціле число b, 0<b<n. Спочаткуобчислюємо
, t непарне, і виберемовипадкове ціле число b, 0<b<n. Спочаткуобчислюємо 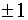 , то висновком, що n пройшло тест (2) при даномуb, іробимо новий випадковий вибір b. В іншому випадку зводимо
, то висновком, що n пройшло тест (2) при даномуb, іробимо новий випадковий вибір b. В іншому випадку зводимо 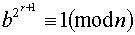 , у той часяк
, у той часяк 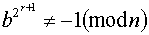 , то n не проходить тест, іце доводить, що n - складене число. Якщо ми k раз випадково вибирали різі основи b і n кожен раз проходило відповідний тест, то число n має не більше
, то n не проходить тест, іце доводить, що n - складене число. Якщо ми k раз випадково вибирали різі основи b і n кожен раз проходило відповідний тест, то число n має не більше 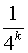 шансу бутискладеним.
шансу бутискладеним.