
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Методи генерації псевдовипадкових послідовностей.147 167 165 171. Випадкова послідовність видала числа:342 076 543 132. У результаті додавання за числах першого і другого отриманий результат:489 243 708 303. Цей результат пересилається одержувачу. Провівши з результату посимвольної віднімання чисел випадкової послідовності одержувач визначає код посланого слова. До сказаного слід додати, що для спрощення викладу вище використовувалися десяткові числа, хоча в реальності програми працюють з двійковими числами.М-послідовності Широке поширення отримали генератори на основі зсувного регістра з лінійними зворотними зв'язками. Вони описуються наступним відношенням: ai = де k - номер такту; ak {0,1} - біти формованої послідовності; ai {0,1} - постійні коефіцієнти; Властивості генерується послідовності визначаються постійними коефіцієнтами ai. Їх можна дослідити, аналізуючи характеристичний поліном g(x) = 1 Å a1 x Å a2 x2Å...Å am-1 xm-1Å am xm. При відповідному виборі коефіцієнтів генерується послідовність {ai} буде мати максимально можливий період, рівний 2m-1, де m - розрядність зсувного регістра і одночасно старша ступінь породжує полінома. Послідовність максимально можливого періоду називається M-послідовністю. Основна задача синтезу генератора розглянутого типу - знаходження характеристичного полінома, що формує М-послідовність.  Поліноми, що формують послідовність максимального періоду, називаються примітивними. Зі зростанням m їх кількість стає дуже великим. Серед безлічі примітивних поліномів ступеня m можна знайти поліноми з найменшим числом одиничних коефіцієнтів ai. Генератори, побудовані на їх основі, мають найбільш просту технічну реалізацію. У табл. 2.1 наведено перелік поліномів з мінімальною кількістю ненульових коефіцієнтів для значень m <= 16. Для формування M-послідовності поряд з примітивним поліномом g (x) може використовуватися і зворотний йому поліном g-1(x)=xmg(x-1). Отримана в цьому випадку послідовність максимальної довжини буде інверсної по відношенню до послідовності, що формується g (x). Наприклад, для полінома g(x)=1Åx3Åx4зворотнім поліномом буде g-1(x) = x4(1Åx-3Åx-4 )=1 Å x Å x4 . Головна перевага описуваного методу формування псевдовипадкових послідовностей - простота його реалізації. Генератор M-послідовності містить лише m-розрядний регістр зсуву та набір суматорів за модулем два в ланцюзі зворотного зв'язку. Регістр зсуву виконує функції зберігання m біт M-послідовності і зсуву m-розрядного коду на один розряд вправо. Суматори за модулем два обчислюють чергове значення молодшого розряду сдвигового регістру. Стан розрядів регістра на кожному такті можна представити у вигляді m-мірних векторів A(k)=a1(k)a2(k)a3(k)...am(k), де k=0,1,2,... - номер такту, ai(k) - стан i-го розряду, i=1,m, Послідовне застосування співвідношень (1) або (2) для s = 0 дозволяє формувати відповідно одно-або багаторозрядних псевдовипадкові послідовності, які характеризується низкою статичних властивостей. Розглянемо найбільш важливі властивості М-послідовностей. 1. Період послідовності, описуваної виразом (1), визначається старшої ступенем породжує полінома g (x) і дорівнює L= 2m -1. 2. Для заданого полінома g (x) існує L різних M-послідовностей, що відрізняються фазовим зсувом. Так, полиному g(x)=1Åx3Åx4відповідає 15 M-послідовностей. 3. Кількість одиничних і нульових символів ak, k=0,1,..., L-1, M- послідовності відповідно дорівнює 2m-1 и 2m-1 -1. Ймовірна оцінка частоти їх появи визначається наступними виразами: p(ak=1)=2m-1 /(2m-1)=1/2 + 1/(2m+1-2), p(ak=0)=(2m-1-1)/(2m-1) = 1/2-(2m+1 -2) і при збільшенні m досягає значень, як завгодно близьких до 1/2. 4. Ймовірності появи серій з r, r 5. Для будь-якого значення s ( 1 Використання лінійних зсувних регістрів для створення криптосистем передбачає їх вразливість, якщо зломщик має парою: вихідний текст - шифротекст довжиною не менше 2m бит. Дійсно, маючивихідний текст M=(m1,m2,...,m2m) івідповідний шифротекст C=(c1,c2,...,c2m), ми можемоотримати К=MÅC=(m1Åc1,m2Åc2,...,m2mÅc2m)=(k1,k2,k3,...,k2m). Тоді завдання злому криптосистеми при відомому початковому стані зводиться до розв'язання системи з m лінійних рівнянь з m невідомими, де невідомими є коефіцієнти породжує полінома. Дана система має вигляд
.... ....
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 747. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Åak ai-k, k=0,1,2,... , (2.1)
Åak ai-k, k=0,1,2,... , (2.1) Å - операція підсумовування за модулем 2. Генератор, описуваний відношенням (2.1), показаний на рис. 2.1.
Å - операція підсумовування за модулем 2. Генератор, описуваний відношенням (2.1), показаний на рис. 2.1.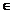 {1,2,...,m-1}, однакових символів (нулів чи одиниць) в M-послідовності максимально близькі до відповідних ймовірностями для випадкової послідовності.
{1,2,...,m-1}, однакових символів (нулів чи одиниць) в M-послідовності максимально близькі до відповідних ймовірностями для випадкової послідовності. s<L ) існує таке r
s<L ) існує таке r 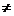 s ( 1
s ( 1  1k1 Å
1k1 Å