
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Энергия электростатического поля. ⇐ ПредыдущаяСтр 5 из 5 Всякий конденсатор при заряде поглощает некоторое количество энергии от источника питания. Эту энергию он накапливает в электрическом поле, имеющимся в его диэлектрике. Определим величину этой энергии для плоского конденсатора. По мере заряда конденсатора растёт его q, получаемый от источника питания и растёт U на его обкладках. q = c Работа, которую совершил источник по переносу заряда на на конденсаторе при его зарядке численно равна площади ∆ ОQB, у которого: Основание ─ Q ─ полный заряд конденсатора. Высота ─U ─ напряжение на конденсаторе после окончания зарядки.
Заменив q на его значение, а C ─ Фарада U ─ Вольт W ─ Джоуль Энергия электростатического поля распределена по всему объёму этого поля с конечной плотностью, величина которого ~
Е ─Напряженность электростатического поля в В/М
Если электростатическое поле однородное, то W = V ─ объём в Пример: Требуется определить энергию, запасённую в электростатическом поле плоского конденсатора, если площадь каждой из обкладок S = 0,004 Е Энергия поля равна Объём электростатического поля: V =S  Энергия, запасённая конденсатором: W Контрольные вопросы: 1.Изобразите картину электрического поля положительного точечного заряда. В каком направлении станет перемещаться пробный отрицательный заряд, помещенный в такое поле. 2.Какое поле называется электростатическим? 3.Что такое напряженность электрического поля?
. Законы Кирхгофа
для узла с : I1 + I2 для узла f : I3 По этому методу число составленных уравнений должно быть на единицу меньше, чем число узлов. На этой схеме 2 узла, значит должно быть одно уравнение. Всего для определения трех токов необходимо три уравнения. Остальные две составляем на основе второго закона Кирхгофа. Определим потенциал точки a, совершив обход по контуру по часовой стрелке:
Перенесем Е в одну часть уравнения: E1 В общем виде: Алгебраическая сумма ЭДС равна алгебраической сумме падений напряжения этого контура. Для контура ƒcde: E2 = I2rвт.2 + I2R2 + I3R3
I1 + I2 + I3 = 0 Цепь имеет три ветви, поэтому нужно составить еще два независимых контурных уравнения (по второму закону Кирхгофа). Для контура с ветвями 1 и 2 E1 + E2 = R1I1 Для контура с ветвями 2 и 3 (это новая ветвь)
После подстановки численных значений Е1 = 225 В, Е2 = 200 В, R1 = R2 = 1 Ом, R3 = 2 Ом. Получаем систему трех уравнений с тремя неизвестными токами I1, I2, I3. I1 + I2 + I3 = 0 225 + 200 = 1I1
Подставим ток I1 = -I2 – I3 из первого уравнения во второе и получим систему двух уравнений 425 = -2I2
Умножим последнее уравнение на 2 и сложим со вторым: 25 = -5I3 откуда I3 = -5A и из последнего уравнения
Из узлового уравнения определим I1= 215 A Мощность, развиваемая первым источником Pист1 = Е1 У второго источника I3 направлено против ЭДС, но численное значение этого тока отрицательное, т.е. действительное направление тока I2 совпадает с направлением ЭДС. Поэтому и второй источник работает в режиме генератора с разветвленной мощностью: Pист2 = Е2 Мощность и преобразования электрической энергии в другие виды, в приемниках P1 = R1I1 P2 = R2I2 P3 = R3I3 Составим баланс мощностей Pист1 + Pист2 = P1 + P2 + P3 или 90375 = 90375 Что подтверждает правильность расчетов токов.
Метод узловых потенциалов (напряжений). Метод узловых потенциалов требует совместного решения меньшего числа независимых уравнений по сравнению с методом узловых и контурных уравнений, что сокращает расчеты. Он основан на применении первого закона Кирхгофа, обобщенного закона Ома. Рассмотрим его применении для отдельных ветвей, представленных на рисунках:
1. Запишем потенциалы точек а и с :
2. Определим токи через разности потенциалов: I1 = Эти зависимости токов от напряжения между выводами ветви и её параметрами называются обобщенным законом Ома.
Расчет токов методом узловых потенциалов. Рассмотрим на примере:
Для двух узлов можно составить независимую систему уравнений по первому закону Кирхгофа. Например: для узлов А и Б I1 – I4 – I3 = 0 ; -I1 + I4 + I5 – I2 = 0 Токи I1 и I2 запишем по обобщенному закону Ома: I1 = а остальные токи по закону Ома: I3 = Потенциал одной из точек можно принять равным нулю. Например, 1) Для узла А: 2) Для узла Б: Если заменить сопротивления ветвей проводимостью: g = 1) Для узла А: (g1 + g4 + g3) 2) Для узла Б: Из полученной системы уравнений после совместного решения определяются неизвестные величины, а именно потенциалы узлов Сумма проводимостей ветвей, присоединенных к узлу, называется собственной узловой проводимостью: gА = g1 + g3 + g4, т.к. к узлу А присоединены 1-я, 3-я, и 4-я ветви. Сумма проводимостей ветвей, соединяющих два узла, называется общей узловой проводимостью: gАБ = g1 + g4. Систему уравнений (1)и (2) можно составить сразу, учитывая что собственная проводимость входит со знаком “+” , а перед общей проводимостью стоит знак “ В правой части в общем случае записываются алгебраические суммы произведений gЕ (со знаком “+” для ЭДС, направленных к узлу, для которого составляется уравнение, и со знаком “
Таким образом, уравнение для данного узла содержит произведение потенциала узла на сумму проводимостей всех ветвей, присоединенных к этому узлу, и произведения потенциалов других узлов на общие проводимости.
Пример расчета.
Методом узловых потенциалов определить токи в цепи с параметрами: R1 = 2 Ом; R2 = 10 Ом; R3 = R5 = 4 Ом; rвт4 = 1 Ом; R4 = 3 Ом; Е'1 = 2 В; Е"2 = 20 В; Е4 = 4 В; Е5 = 6 В; Решение. Для цепи с тремя узлами нужно составить два узловых уравнения, например, для узлов А и Б: (предварительно выбрав положительные направления токов). Для узла А: Для узла Б: Каждый из токов запишем по обобщенному закону Ома или по закону Ома: I1 = I2 = I3 = I4 = I5 = Подставим эти значения токов в узловые уравнения: 0,5
или 1,1
Из полученных двух уравнений находим неизвестные потенциалы:
Последнюю систему уравнений можно составить сразу. Например: в 1- Ом уравнении: 1) Сумма проводимостей ветвей, присоединенных к узлу А: gА = g1 + g2 + g3 + g4 = 0,1 + 0,5 + 0,25 + 0,25 (См); 2) Сумма проводимостей ветвей, соединяющих узлы А и Б: gАБ = g3 + g4 = 0,25 + 0,25 (См);
3) Сумма проводимостей ветвей, присоединенных к узлу Б: gБ = g3 + g4 + g5 = 0,25 + 0,25 + 0,25 (См);
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 763. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 q=c
q=c  на W, получим W =
на W, получим W = 
 , т. е.
, т. е. =
= 
 ─ Объёмная плотность энергии поля в Дж/
─ Объёмная плотность энергии поля в Дж/  ─ 8, 85
─ 8, 85  Ф/м ─ диэлектрическая проницаемость вакуума.
Ф/м ─ диэлектрическая проницаемость вакуума. ─ относительная диэлектрическая проницаемость среды, где распределено электростатическое поле.
─ относительная диэлектрическая проницаемость среды, где распределено электростатическое поле.
 V = S
V = S 
 = 5 и U на обкладках равно 120 Вольт. Электростатическое поле можно считать однородным.
= 5 и U на обкладках равно 120 Вольт. Электростатическое поле можно считать однородным.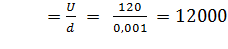
 =
=  = 0,318 Дж/
= 0,318 Дж/ 
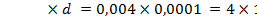
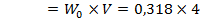 Дж.
Дж.

 I3 = 0
I3 = 0 I2
I2  a =
a =  =
= 

 5 т.е. I2 = -200 A
5 т.е. I2 = -200 A = 1
= 1 
 а =
а =  Е2 + R2I2
Е2 + R2I2 =
=  ; I2 =
; I2 =  =
=  ;
;
 ; I2 =
; I2 = 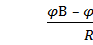 ;
; ; I4 =
; I4 = 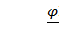 ;
;
 = 0;
= 0;

 = 0;
= 0; (См), и перенести слагаемые с ЭДС в правую часть уравнения, то получим:
(См), и перенести слагаемые с ЭДС в правую часть уравнения, то получим: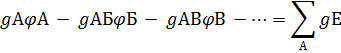

 =
=  =
=  =
=  = 0,1
= 0,1  A;
A; =
=  =
=  = 0,25
= 0,25  =
=  = 0,25
= 0,25  = g1Е1 – g4Е4 = 0,5
= g1Е1 – g4Е4 = 0,5