
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
При этом стержень 2 будет нагружен максимально и равно 160 МПа, а в стержне 1 будут действовать напряжения, равные 144.0 МПа. ⇐ ПредыдущаяСтр 2 из 2
ЗАДАЧА 25
Для стального вала постоянного поперечного сечения определить значения крутящих моментов на валу, построить эпюру крутящих моментов и определить диаметр вала в опасном сечении из расчета на прочность и жесткость.
Р1=40 кВт; Р2=120 кВт; Р3=20 кВт; w=20 рад/с; [φ0] = 0.02 рад/м; [tк] =30 МПа; G=8×104МПа; сечение круглое. Решение: Определим мощность на втором шкиве
1. Определим крутящие моменты на валу по формуле
Построим эпюру крутящих моментов по участкам вала
2. Определим требуемый диаметр вала из расчета на кручение (прочность) по максимальному крутящему моменту на участке вала (участок II).
3. Определим требуемый диаметр вала из расчета на жесткость.
Требуемый размер сечения получился больше из расчёта на прочность поэтому из двух рассчитанных значений диаметра вала выбираем наибольшее. Ответ: требуется вал d=80 мм. ЗАДАЧА 33
Для стальной балки, жестко защемленной одним концом, построить эпюры поперечных сил и изгибающих моментов и подобрать из условия прочности необходимый размер двутавра, приняв [s]=160 МПа
Дано: схема 3; F=10 кН; М=10 кНм; q=10 кН/м . Решение: 1. Разобьем балку на участки. 2. При помощи метода сечений построим эпюру поперечных сил. QI=0; QII=F=10 кН; QIII=F-q×(x-2). При x=6 м QIII=F-q×4=10-10×(6-2) =-30 кН. Найдем точку перехода эпюры через нулевую линию на третьем участке
3. При помощи метода сечений построим эпюру изгибающих моментов. МI=М=10 кНм; МII=М-F×1=10-10×1=0; МIII(x)=М-F×(x-1) +q×(x-2)2=10-10×(3-1) +10×0.5×(3-2)2=-5 кНм;  МIII=М-F×(x-1) +q×(x-2)2=10-10×(6-1) +10×0.5×(6-2)2=40 кНм; Мmax=МIII= 40кНм.
4. Подберем необходимый размер двутавровой балки
По справочнику принимаем двутавр №24 ГОСТ 8239-89 WX=289 см3, что больше, требуемого момента сопротивления. Вычисляем недогрузку ∆:
Ответ: требуется балка двутавр №24 ГОСТ 8239-89. ЗАДАЧА 41
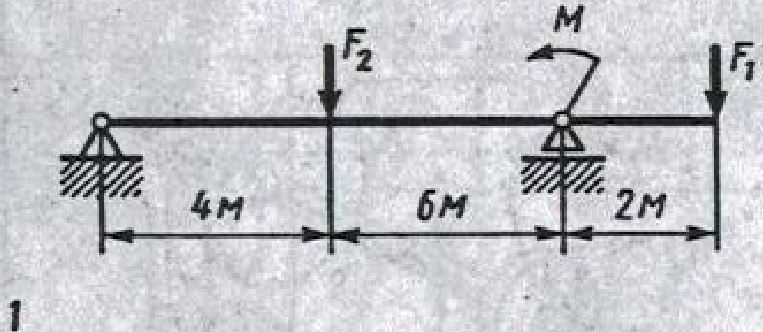
Для двухопорной балки построить эпюры поперечных сил, изгибающих моментови подобрать из условия прочности размеры поперечного сечения прямоугольника или круга, приняв для прямоугольникаh=2b, считать[s]=150 МПа.
схема 1; F1=10 кН; F2=20 кН; M=15 кНм; [s]=150 МПа. Решение: 1. Составим расчетную схему задачи. 2. Выберем оси координат. 3. Составим уравнения статического равновесия балки.
4. Найдем из уравнений статического равновесия искомые величины. Из (1) Из (2) Проверка: 5. Разобьем балку на участки. 6. При помощи метода сечений построим эпюру поперечных сил. Для I участка QI=F1=10 кН; Для II участка QII=F1-RA=10-18.5=-8.5 кН; Для III участка QIII=F1-RA+F2=10-18.5+20=11.5 кН. 7. При помощи метода сечений построим эпюры изгибающих моментов. Для I участка МI=-F1×2=-10×2=-20 кНм; Для II участка МI/=-F1×2+M=-10×2+15=-5 кНм; Для III участка МIII=-F1×8+RA×6+M=-10×8+18.5×6+15=46 кНм. Мmax=46 кНм.
8. Подберем сечение балки.
Для балки прямоугольного сечения с соотношением сторон h = 2b
Откуда Тогда h=2b=2×8=16 см. Ответ: RA=18.5 кН; RB=11.5 кН; МMAX=46 кНм;требуется балка сечения h/b=16/8 см.
ЗАДАЧА 52
Для стального вала постоянного поперечного сечения с двумя зубчатыми колесами, передающего мощность Р при заданной угловой скорости определить вертикальные и горизонтальные составляющие реакций подшипников, определить диаметр вала. Расчет производить по гипотезе потенциальной энергии формоизменения.
Fr1=0.4F1; Fr2=0.4F2; P=10 кВт; w=50 рад/с; [s]=70 МПа. Решение: 1. Составим расчетную схему задачи. 2. Выберем оси координат. 3. Определим крутящий момент на валу по формуле
4. Определим силы в зацеплениях.
5. Составим уравнения статического равновесия балки. Вертикальная плоскость YOZ
Горизонтальная плоскостьXOZ 6. Найдем из уравнений статического равновесия искомые величины. Из (1) Из (2) Из (3) Из (4) 7. Построим эпюры моментов. Крутящие моменты. Мкр=200 Нм. Изгибающие моменты Вертикальная плоскость YOZ М2=0.06×YA=0.06×1317»79.0 Нм. М1=0.06×YB=0.06×1269.3»76.2 Нм. Горизонтальная плоскость XOZ М2=-0.06×XA=-0.06×1333.3=-80.0 Нм. М1=-0.06×XB=-0.06×2400=-144.0 Нм.
8. Определим суммарный изгибающий момент в наиболее опасном сечении под колесом 1
9. По гипотезе потенциальной энергии формоизменения определяем эквивалентный момент
10. Определим требуемый момент сопротивления кручению для балки.
Для круга W=pd3/32. Из чего следует Принимаем d=35 мм. Ответ: XA=1333.3 Нм; YA=1317 Нм; XB=2400 Нм; YB=1269.3 Нм; d=35 мм.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. Аркуша А.И. Техническая механика. Теоретическая механика и сопротивление материалов. – М.: Высшая школа, 2002. 2. Багреев В.В., Винокуров А.И., Киселев В.А. Сборник по технической механике. – Л.: Высшая школа, 1975. 3. Винокуров А.И., Барановский Н.В. Сборник задач по сопротивлению материалов. – М.: Высшая школа, 1990. 4. Дубейковский Е.Н., Саввушкин Е.С. Сопротивление материалов. – М.: Высшая школа, 1985. 5. Ицкович Г.М. Сопротивление материалов. – М.: Высшая школа, 1988. 6. Никитин Г.М. Теоретическая механика для техникумов. – М.: Наука, 1988. 7. Файн А.М. Сборник задач по теоретической механике. – М.: Высшая школа, 1987. 8. Эрдеди А.А. и др. Техническая механика. – М.: Высшая школа, 1992. 9. Мишенин Б.В. Техническая механика. Задания на расчетно-графические работы для ССУзов с примерами их выполнения. – М.: НМЦ СПО РФ, 1994. 10. Куклин Н.Г., Куклина Г.С. Детали машин. – М.: Машиностроение, 1987. 11. Фролов М.И. Техническая механика. Детали машин. – М.: Высшая школа, 1987. 12. Романов Н.Я., Константинов В.А., Покровский Н.А. Сборник задач по деталям машин. М.: Машиностроение, 1984.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 1286. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
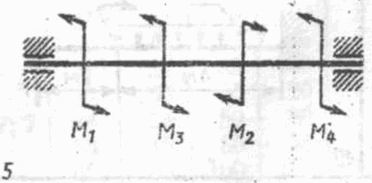 Дано: схема 5;
Дано: схема 5; кВт.
кВт. Нм;
Нм; Нм;
Нм; Нм;
Нм; Нм;
Нм; Нм.
Нм.

 м. Принимаем dкр=80 мм.
м. Принимаем dкр=80 мм. м. Принимаем dж=70 мм.
м. Принимаем dж=70 мм.
 м.
м.
 см3.
см3.
 Дано:
Дано:
 кН.
кН.


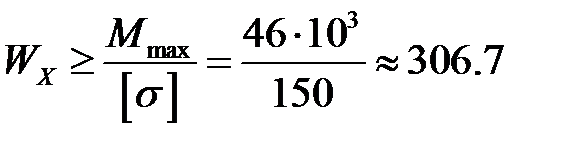 см3.
см3. .
. см. Принимаем b=8 см.
см. Принимаем b=8 см. Дано: схема 2;
Дано: схема 2; Нм.
Нм.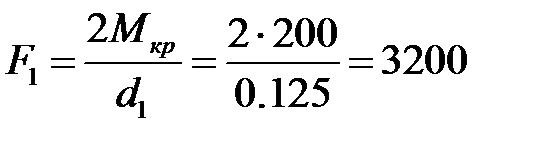 Н;
Н; Н;
Н; Н;
Н; Н.
Н.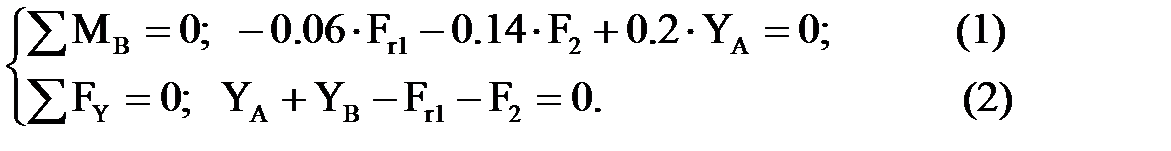

 Н.
Н. Н.
Н. Н.
Н. Н.
Н.
 Нм.
Нм. Нм.
Нм.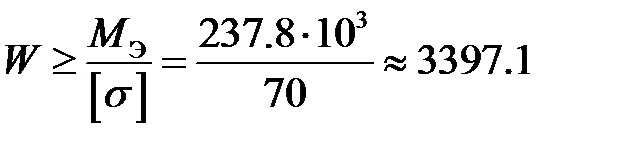 мм3.
мм3.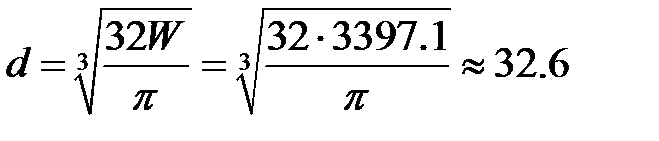 мм.
мм.