Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Экономико-математическая модельСтр 1 из 2Следующая ⇒ Содержание 1. Задание 9.1 2. Задание 9.2
Задание 9.1 Постановка экономической задачи Оптимальный план развития программных продуктов. Компания “Корвет” производит программное обеспечение на CD-ROM. Компания оценивает возможность развития шести новых программных приложений. В таблице представлена информация о затратах и ожидаемой чистой прибыли о продажи приложений (тыс. долл.)
У “Корвета” 60 программистов. На развитие новых программных приложений фирма может выделить 3,5 млн. долларов. Каков оптимальный набор приложений, которые следует развивать, если: 1) ожидается, что клиенты, заинтересованные в приложении П4, будут также заинтересованы в приложении П5 и наоборот. Таким образом, эти приложения должны либо вместе развиваться, либо вместе не развиваться; 2) развитие приложения П1 имеет смысл только при наличии приложения П2. Таким образом, если развивается приложение П1, должно развиваться и приложение П2, но приложение П2 может развиваться и без приложения П1; 3) развиваться может только одно из приложений П3 и П6 4) стремясь обеспечить качество продукции, “Корвет” не склонен развивать более трёх программных продуктов. Проанализируйте влияние каждого из четырёх перечисленных ограничений на оптимальное решение. Решение: Экономико-математическая модель Обозначим через Х1,Х2,Х3,Х4,Х5,Х6 предложение каждого типа.  Целевая функция – это выражение, которое необходимо максимизировать: F(X)=X1*2000+X2*3600+X3*4000+X4*3000+X5*4400+X6*6200 F(X)=X1*400+X2*1100+X3*940+X4*760+X5*1260+X6*1800≤3500 F(X)=X1*6+X2*18+X3*20+X4*16+X5*28+X6*34≤60 Xi – двоичное Ограничения по ресурсам: 1) X4=X5 2) X1≤X2 3)3+X6=1 4)X1+X2+X3+X4+X5+X6≤3 В данной задаче оптимизационные значения вектора Х=(Х1,Х2,Х3,Х4,Х5,Х6) будут помещены в ячейках В2:В7. Оптимальное значение функции будет находиться в ячейке В12. Расположение исходных данных на листе MS EXCEL показано на рис.1
Рис. 1 Исходные данные 1)Только первое ограничение: Вводим зависимость для целевой функции: - Поместить курсор в ячейку В16 - из меню Мастер функций выбираем функцию СУММПРОИЗВ - Появляется диалоговое окно СУММПРОИЗВ, в строке Массив1 вводим В$2:В$7, в строке Массив2 вводим E$2:Е$7 -Нажимаем ОК.
Рис. 2 Ввод функции Аналогичные действия проделываем ещё с несколькими ячейками. Чтобы просмотреть какие именно, преобразуем лист так, чтобы присутствовало отображение формул: В меню “Сервис” выбираем “Параметры”, ставим флажок “Формулы”. Параметры представлены на рис. 3.
Рис.3 Параметры Полученный результат представлен на рис. 4
Рис. 4 Режим отображения формул Далее запускаем команду Поиск решения и вводим условия для первого ограничения(Рис.5):
Рис.5 Ввод условий первого ограничения
И нажав “Выполнить” получаем результат, представленный на рис. 6:
Рис. 6 Первое ограничение 2) Только второе ограничение: - Чистим ячейки В2:В7 выделяя их и нажимая “Delete” - запускаем команду Поиск решения и вводим условия для второго ограничения(Рис.7):
Рис. 7 Ввод условий второго ограничения И нажав “Выполнить” получаем результат, представленный на рис. 8:
- Чистим ячейки В2:В7 выделяя их и нажимая “Delete” - запускаем команду Поиск решения и вводим условия для третьего ограничения(Рис.9):
Рис. 9 Ввод условий третьего ограничения И нажав “Выполнить” получаем результат, представленный на рис. 10:
Рис. 10 Третье ограничение 3) Только четвёртое ограничение: - Чистим ячейки В2:В7 выделяя их и нажимая “Delete” - запускаем команду Поиск решения и вводим условия для четвёртого ограничения(Рис.11):
Рис. 11 Ввод условий четвёртого ограничения И нажав “Выполнить” получаем результат, представленный на рис. 12:
Рис. 12 Четвёртое ограничение • В электронной таблице появился дополнительный лист Отчет по устойчивости (рис.13).
Рис.13. Отчет по устойчивости.
Вывод: Ограничения 1,4 и 2,3 схожи. При этом ограничения 2 ,3 существеннее влияют на положительное решение. Задание 9.2 Транспортная задача. Требуется минимизировать расходы на доставку продукции заказчикам (магазинам) со складов фирмы, учитывая приведённые в таблице тарифы на перевозку продукции, объём заказа и количество продукции, хранящейся на каждом складе.
1. Предложить план перевозок, который обеспечивает минимальные совокупные транспортные издержки. 2. Что произойдёт с оптимальным планом, если изменятся условия перевозок: а) появится запрет на перевозки со склада С1 до магазина “Шер”; б) по этой коммуникации будет ограничен объём перевозок – 3т? Решение: |
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 1175. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||
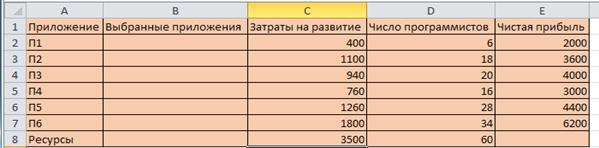
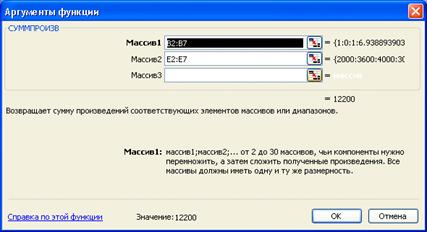





 Рис. 8 Второе ограничение
Рис. 8 Второе ограничение