
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ТЕХНОЛОГИЯ МОДЕЛИРОВАНИЯ С УЧЕТОМ УПРАВЛЕНИЯ МОДЕЛЬНЫМ ВРЕМЕНЕМ ⇐ ПредыдущаяСтр 4 из 4 При разработке практически любой имитационной модели и планировании проведения модельных экспериментов необходимо соотносить между собой три представления времени: • реальное время, в котором происходит функционирование имитируемой системы; • модельное (или, как его еще называют, системное) время, в масштабе которого организуется работа модели; • машинное время, отражающее затраты времени ЭВМ на проведение имитации. С помощью механизма модельного времени решаются следующие задачи: 1) отображается переход моделируемой системы из одного состояния в другое; 2) производится синхронизация работы компонент модели; 3) изменяется масштаб времени «жизни» (функционирования) исследуемой системы; 4) производится управление ходом модельного эксперимента; 5) моделируется квазипараллельная реализация событий в модели. Необходимость решения последней задачи связана с тем, что в распоряжении исследователя находится, как правило, однопроцессорная вычислительная система, а модель может содержать значительно большее число одновременно работающих подсистем. Поэтому действительно параллельная (одновременная) реализация всех компонент модели невозможна. Даже если используется так называемая распределенная модель, реализуемая на нескольких узлах вычислительной сети, совсем необязательно число узлов будет совпадать с числом одновременно работающих компонент модели. Существуют два метода реализации механизма модельного времени — с постоянным шагом и по особым состояниям. Выбор метода реализации механизма модельного времени зависит от назначения модели, ее сложности, характера исследуемых процессов, требуемой точности результатов и т. д.  При использовании методапостоянного шага отсчет системного времени ведется через фиксированные, выбранные исследователем интервалы времени. События в модели считаются наступившими в момент окончания этого интервала. Погрешность в измерении временных характеристик системы в этом случае зависит от величины шага моделирования ∆t. Метод постоянного шага предпочтительнее, если: • события появляются регулярно, их распределение во времени достаточно равномерно; • число событий велико и моменты их появления близки; • невозможно заранее определить моменты появления событий. Данный метод управления модельным временем достаточно просто реализовать в том случае, когда условия появления событий всех типов в модели можно представить как функцию времени. Выбор величины шага моделирования является нелегким и очень важным делом. Универсальной методики решения этой проблемы не существует, но во многих случаях можно использовать один из следующих подходов: • принимать величину шага равной средней интенсивности возникновения событий различных типов; • выбирать величину Dt равной среднему интервалу между наиболее частыми (или наиболее важными) событиями. При моделированиипо особым состояниям системное время каждый раз изменяется на величину, строго соответствующую интервалу времени до момента наступления очередного события. В этом случае события обрабатываются в порядке их наступления, а одновременно наступившими считаются только те, которые являются одновременными в действительности. Метод моделирования по особым состояниям сложнее в реализации, так как для него требуется разработка специальной процедуры планирования событий (так называемого календаря событий). Моделирование по особым состояниям целесообразно использовать, если: • события распределяются во времени неравномерно или интервалы между ними велики; • предъявляются повышенные требования к точности определения взаимного положения событий во времени; • необходимо реализовать квазипараллельную обработку одновременных событии. Дополнительное достоинство метода заключается в том, что он позволяет экономить машинное время, особенно при моделировании систем периодического действия, в которых события длительное время могут не наступать.
(
СРЕДСТВА ДЛЯ МОДЕЛИРОВАНИЯ Для описания имитационного процесса весьма важен вопрос выбора языка программирования. Хотя теоретически можно написать модель на любом из распространенных языков программирования высокого уровня, но опыт развития теории и практики имитационного моделирования в нашей стране и за рубежом показывает, что наиболее эффективным средством являются специальные имитационные языки, которых к настоящему времени создано уже немало и многие из них эффективно используются, особенно за рубежом, где ни один крупный проект не реализуется без проверки на имитационной модели. Выбор языка моделирования влечёт за собой принятие концепции авторов языка, что не может не сказаться на стратегии разработки, построения и совершенствования модели, ибо этот процесс существенно зависит от гибкости и мощности изобразительных средств языка, ресурсов, предоставляемыми пользователю. Главной функцией имитационной модели является воспроизведение с заданной степенью точности прогнозируемых параметров её функционирования, представляющих исследовательский интерес. Как объект, так и его модель должны обладать системными признаками. Для моделирования на ЭВМ сложной системы нужен аппарат программирования, предусматривающий: - способы организации данных, обеспечивающие простое и эффективное моделирование; - удобные средства формализации и воспроизведения динамических свойств моделируемой системы; - возможности имитации стохастических систем, т.е. процедуры генерирования и анализа случайных величин и временных рядов. Реализация требований к имитационным моделям в рамках универсального языка программирования приводит к громоздким и неудобным для практического использования программам. В большинстве таких программ могут разобраться только их авторы, а любое изменение в постановке задачи требует переработки значительной части текста программы. При создании специальных языков для ИМ можно выделить несколько следующих классов языков, которые соответствуют определенным признакам: 1. Доработка универсального языка группы операторов, реализующих дополнительные для моделирования функции. GASP 2. Языки, обрабатывающие и использующие аппарат дифференциальных уравнений. DYNAMO 3. Языки, предназначенные для моделирования дискретных систем. GPSS – простота и наглядность. Пока ИМ применялось как метод исследования в научной деятельности и крайне редко в практической работе, такие языки устраивали всех, однако по мере расширения практических задач, когда процедуры моделирования все больше стали применяться в практической работе, потребовались языки моделирования боле применимые в практической деятельности. В конце века появились и получили широкое распространение новое поколение языков. Наиболее распространенные пакеты:
1. Process Charter – 1.0. США, Калифорния 2. PowerSim – 2.01 3. Extend+BPR – 3.0 4. Rethink 5. Piligrim
Process Charter ориентирован на дискретное моделирование, удобен и прост в построении модели. Самый дешевый, слабо пригоден для моделирования непрерывных процессов. PowerSim является лучшим в непрерывных моделях. Множество встроенных функций. Extend+BPR. Данный пакет предназначен для создания и моделирования бизнес-проектов.
СЛУЧАЙНЫЕ ПРОЦЕССЫ Реально бОльшая часть систем и устройств находится под воздействием неизвестных факторов. Поскольку с течением времени действия этих факторов меняются, то предсказать поведение исследуемых процессов заранее также невозможно. Величины, которые приводились в примерах, представляют собой случайные функции времени. В результате конкретного опыта случайная функция превратится в обычную неслучайную. Во втором примере состояние системы не характеризуется числовой величиной, а описывается качественно: процесс функционирования этой системы сводится к случайной смене состояний и блужданию по состоянию.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 670. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
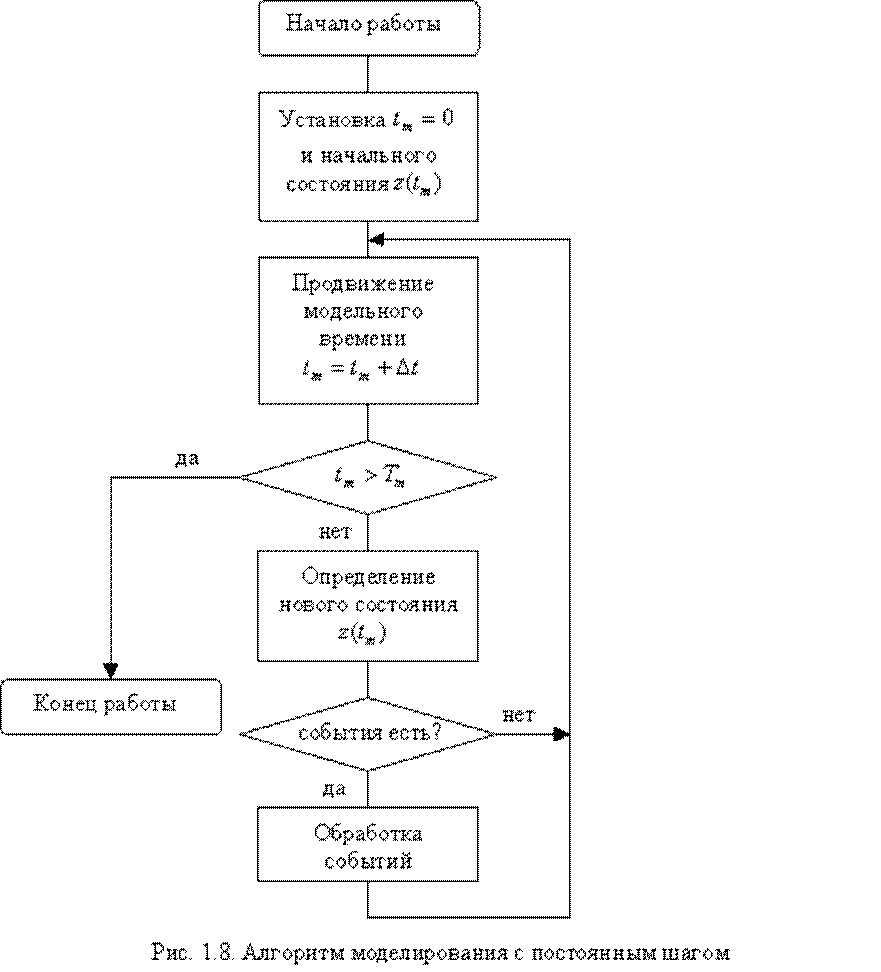
 — текущее значение модельного времени,
— текущее значение модельного времени,  — интервал моделирования).
— интервал моделирования).
 - прогнозируемый момент наступления
- прогнозируемый момент наступления  -го события.
-го события.