
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Электронная логическая схема операции НЕ.Стр 1 из 14Следующая ⇒ Инверсия Над переменном в булевой алгебре можно производить только три действия: дизъю́нкция(логическое сложение ),конъюнкцию(логическое умножение), и инверсию(логическая отрицаниие) Инверсия - это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО. Таблица истинности для инверсии
4) Переместительный закон Сумма не изменяется от перемены порядка слагаемых. a + b = b + a, где a и b – любые числа. Из арифметики известно, что переместительный закон верен для суммы любого числа слагаемых. Сочетательный закон Сумма нескольких слагаемых не изменится, если какую-нибудь группу рядом стоящих слагаемых заменить их суммой. Для суммы трех слагаемых имеем: (a + b) + c = a + (b + c). Например, сумму 5 + 7 + 11 можно вычислить двумя способами так: (5 + 7) + 11 = 12 + 11 = 23,
Распределительный закон Это очень важный закон, который при умелом применении позволяет экономить много времени при вычислениях, решении уравнений и многом другом. Закон звучит и записывается так: Чтобы умножить сумму (или разность) на число, можно отдельно умножить на это число каждое слагаемое (уменьшаемое и вычитаемое) и полученные произведения сложить (вычесть). Буквенные записи законов выглядят так:
Буквенную запись законов нужно обязательно выучить.  В учебнике есть много примеров применения данного закона. Добавлю ещё несколько примеров, которые на первый взгляд выглядят страшно, но распределительный закон позволяет решить их устно. Распределительный (дистрибутивный)закон умноженияотносительно сложения: ( m + n ) · k = m · k + n · k . Этот закон фактически расширяет правила действий со скобками Правило. Чтобы умножить число на сумму, можно умножить это число на каждое из слагаемых и полученные произведения сложить. Например: 7 * (6 + 5) = 7 * 6 + 7 * 5 = 77 a * (b + c) = ab + ac Распределительный закон распространяется и на действие вычитания. Например: 7 * (6 — 5) = 7 * 6 — 7 * 5 = 7 Законы умножении распространяются на любое количество множителей в числовом или буквенном выражении. Распределительный закон умножения используется для вынесения общего множителя за скобки. Правило. Чтобы преобразовать сумму (разность) в произведение, достаточно вынести за скобки одинаковый множитель слагаемых, а оставшиеся множители записать в скобках суммой (разностью). Например: 7 * 8 — 7 * 5 = 7 * (8 — 5) аЬ + ас = а * (Ь + с) Вынесение множителя за скобки для больших числовых или буквенных выражений можно производить по группам слагаемых. Например: 3 * 6 + 9 * 6 — 4 * 8 = 6 * (3 + 9) — 4 * 8 ab + bc — df -af = b * (a + c) — f * (d + a) c * (a + b) — d * (a + b) = (a + b) * (c — d) Законы поглощения Если рассматривать приложение исчисления высказываний для анализа и оптимизации К законам, позволяющим уменьшать элементы и операции логических высказываний, относятся законы поглощения и склеивания. Закон поглощения: для логического сложения: А (A & B) = A; для логического умножения: A & (A B) = A. Знание законов логики позволяет проверять правильность рассуждений и доказательств. Основываясь на законах, можно выполнять упрощение сложных логических выражений. Такой процесс замены сложной логической функции более простой, но равносильной ей, называется минимизацией функции. Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), другие - основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.). Нарушения законов логики приводят к логическим ошибкам и вытекающим из них противоречиям. Правило склеивания
Доказательство (2.11):
Доказательство(2.12):
9. Закон обобщённого склеивания.
Доказательства(2.13): Доказательство (2.14). Раскроем скобки сначала левой части равенства (2.14) а, затем, правой его части.
Правило де Моргана Законы де Моргана (правила де Моргана) — логические правила, связывающие пары дуальных логических операторов при помощи логического отрицания. История и определение Огастес де Морган первоначально заметил, что в классической пропозициональной логике справедливы следующие соотношения: not (P and Q) = (not P) or (not Q) not (P or Q) = (not P) and (not Q) Обычная запись этих законов в формальной логике:
в теории множеств:
Формулы де-Моргана применимы при любом числе аргументов. Они иллюстрируют глубокую взаимную симметрию операций И и ИЛИ: если операция И избирательно реагирует на совпадение прямых сигналов, то операция ИЛИ так же избирательно реагирует на совпадение их инверсий. Элемент ИЛИ прозрачен для любого сигнала, элемент И — для любой инверсии. Пользуясь формулами де-Моргана, можно легко переводить логические схемы из базиса НЕ, И, ИЛИ, в котором человеку привычнее всего мыслить и составлять исходные логические выражения, в инвертирующие базисы, которые эффективнее всего реализуются интегральной технологией.
Стрелка Пирса Стрелка Пирса (логическое «ИЛИ-НЕ») высказываний a и b - это новое высказывание, которое будет истинно тогда и только тогда, когда оба высказывания ложны. Знаком стрелки Пирса является ↓ Значения функции стрелки Пирса представлены в таблице: Логическим элементом операции стрелки Пирса является:
Стре́лка Пи́рса — бинарная логическая операция, булева функция над двумя переменными. Введена в рассмотрение Чарльзом Пирсом (Сharles Peirce) в 1880—1881 г.г. Стрелка Пирса, обычно обозначаемая ↓, эквивалентна операции ИЛИ-НЕ и задаётся следующей таблицей истинности: Таким образом, высказывание «X ↓ Y» означает «ни X, ни Y». От перемены мест операндов результат операции не изменяется.
11. Штрих Ше́ффера — бинарная логическая операция, булева функция над двумя переменными. Введена в рассмотрение Генри Шеффером в 1913 г. (в отдельных источниках именуется как Пунктир Чулкова) Штрих Шеффера, обычно обозначаемый |, эквивалентен операции И-НЕ и задаётся следующей таблицей истинности:
Таким образом, высказывание X | Y означает, что X и Y несовместны, т.е. не являются истинными одновременно. От перемены мест операндов результат операции не изменяется. Штрих Шеффера, как и стрелка Пирса, образует базис для пространства булевых функций от двух переменных. То есть используя только штрих Шеффера можно построить остальные операции. Например,
В электронике это означает, что для реализации всего многообразия схем преобразования сигналов, представляющих логические значения, достаточно одного типового элемента. С другой стороны, такой подход увеличивает сложность реализующих логические выражения схем и тем самым снижает их надёжность. Примером может являться промышленная 155 серия. Элемент 2И-НЕ (2-in NAND), реализующий штрих Шеффера обозначается следующим образом (по стандартам ANSI):
В европейских стандартах принято другое обозначение:
12. Диодные ключи. Общие сведения. Электронный ключ — это устройство, которое может находиться в одном из двух устойчивых состояний: замкнутом или разомкнутом. Основу электронного ключа составляет нелинейный активный элемент (полупроводниковый диод, транзистор, тиристор и др.), работающий в ключевом режиме. По типу используемого нелинейного элемента электронные ключи делятся на диодные, транзисторные, тиристорные и т. д. Диодные ключи. Простейший тип электронных ключей – диодные ключи. В качестве активных элементов в них используются полупроводниковые или электровакуумные диоды. При положительном входном напряжении диод открыт и ток через него
Выходное напряжение
Обычно
где При этом выходное напряжение
Диодные ключи не позволяют электрически разделить управляющую и управляемые цепи, что часто требуется на практике. Для переключения (коммутации) напряжений и токов служат т.н. диодные ключи. Эти схемы позволяют при подаче определенного управляющего напряжения замыкать/размыкать электрическую цепь, по которой передается полезный сигнал (ток, напряжение). В простейших ключевых схемах в качестве управляющего может использоваться сам входной сигнал. Говоря о диодных ключах нельзя не упомянуть особый класс полупроводниковых диодов — p-i-n-диоды. Они применяются только для коммутации ВЧ и СВЧ сигналов. Это возможно благодаря их уникальному свойству — регулируемой проводимости на частоте сигнала. Такое регулирование осуществляется обычно либо при подаче на диод внешнего постоянного напряжения смещения, либо непосредственно уровнем сигнала (для ограничительных p-i-n-диодов). Транзисторные ключи Транзисторные ключи выполняются на биполярных или полевых транзисторах. В свою очередь ключи на полевых транзисторах делятся на МДП-ключи и ключи на полевых транзисторах с управляющим р—га-переходом. Ключи на биполярных транзисторах делятся на насыщенные и ненасыщенные. При анализе транзисторных ключей рассматривают два режима — статический и динамический. В статическом режиме анализируется закрытое и открытое состояние ключа. В закрытом состоянии ключа на его входе низкий уровень напряжения (сигнал логического нуля), при котором оба перехода смещены в обратном направлении (режим отсечки). При этом коллекторный ток определяется только тепловым током. При использовании ключа в логических интегральных схемах, в которых обычно применяются транзисторы типа п—р—п, запирающее напряжение положительно и в этом случае имеет место только "условное" запирание транзистора, когда его эмиттерный переход смещен в прямом направлении; однако уровень действующего на его входе напряжения меньше порогового уровня, равного около 0,6 В, и коллекторный ток транзистора относительно мал, т.е. составляет лишь единицы процентов от тока открытого транзистора. В открытом состоянии ключа на его входе высокий уровень напряжения (сигнал логической единицы). При этом возможны два режима работы открытого транзистора — работа в линейной области выходной характеристики или в области насыщения. В активной области эмиттерный переход смещен в прямом направлении, а коллекторный — в обратном, при этом для кремниевых транзисторов напряжение на эмиттерном переходе составляет около 0,7 В и коллекторный ток практически линейно зависит от тока базы. В области Насыщения оба перехода транзистора смещены в прямом направлении и изменение тока базы не приводит к изменению коллекторного тока. Для кремниевых транзисторов ИС напряжение на смещенном в прямом направлении р—n-переходе составляет около 0,8 В, для германиевых оно равно 0,2...0,4 В. Насыщение ключа достигается увеличением тока базы. Однако при некотором его значении, которое называется базовым током насыщения „, дальнейший рост тока базы практически не приводит к росту коллекторного тока насыщения , при этом напряжение на коллекторе (с учетом коллекторной нагрузки) составляет несколько десятков или сотен милливольт (в ИС около 0,1...0,2 В). Одной из важных характеристик ключа в режиме насыщения является параметр 8 — коэффициент насыщения, равный отношению 1кн/1бн- На границе насыщения 8=1. С увеличением коэффициента насыщения ключа увеличивается его нагрузочная способность, уменьшается влияние различных дестабилизирующих факторов на выходные параметры ключа, но ухудшается быстродействие. Поэтому коэффициент насыщения выбирается из компромиссных соображений, исходя из условий конкретной задачи. Быстродействие ключевого элемента определяется максимально допустимой частотой следования входных переключающих сигналов. Очевидно, что оно зависит от общей длительности переходного процесса, определяемой инерционностью транзистора и влиянием паразитных параметров (например, перезарядом паразитных емкостей в процессе переключения). Часто для характеристики быстродействия ключевого (логического) элемента используется среднее время задержки сигнала при его передаче через элемент. При конечной длительности фронта входного сигнла задержки включения и выключения отсчитываются на 10- или 50-процентных уровнях входного и выходного сигналов. Взаимодействие ключей друг с другом осуществляется через элементы связи. Если уровень напряжения на выходе первого ключа высокий, то на входе другого ключа должен быть уровень, при котором второй ключ открывается и работает в заданном режиме, и, наоборот, если первый ключ открыт, то на входе второго ключа должен быть достаточно низкий уровень, при котором второй ключ закрыт. Цепь связи оказывает существенное влияние на переходные процессы, возникающие при переключении, и, следовательно, на быстродействие ключей.
Электронная логическая схема операции НЕ. Логическая операция «НЕ» основана на отрицании и исключении условия в ответе логической операции. В противопоставлении условия и ответа. «ДА» — «НЕТ». Одно условие и один результат. И результат противоположен условию. 0 – 1 и 1- 0, вот сегодняшняя математическая интерпретация такого противопоставления. Мы задаем условие и получаем его, вроде бы, противоположность. Как результат действия условия. Если «не черное», то – «белое»? Не совсем так. «Не черное» — оно и есть, не черное. Какое угодно, только — не черное. В математике логики есть только две цифры: 0 и 1. Это привело к слиянию нескольких смыслов операции «НЕ» -,противоположности, противопоставления и исключения условия из результата. Вот и осталось одно противопоставление в виде противоположности. Да уж, иная простота – хуже воровства… Далее математика определила свое дополнение: Нет условия и – нет результата. Очень жесткое дополнение. И ограничение. Получается, что ответ в задаче есть, только пока мы решаем эту задачу. Решили, и — ответ пропал. А мы так к нему стремились … Но мы все же запишем ответ. И пусть все условия задачи пропадут, и уйдут из памяти, ответ, вот он – остался. Как результат операции. Это против математического ограничения, но соответствует философской концепции логики. Ответ в задаче должен быть. И если мы его нашли, то он должен остаться. Даже если задача уже не актуальна. Может быть, она для нас уже и не задача, мы же знаем ответ, но для следующих пытливых умов она снова встанет на пути. Знание ответа поможет им пойти дальше, чем довелось нам. Вот на этом и остановимся. Математическое выражение противопоставления, это решаемая нами задача. И у задачи должен быть ответ, как результат её решения. Отдельно от выражения. Сам по себе. Уже, как событие для следующей задачи.
Рис.50. Счетное «НЕ». В качестве элемента счетного «противоположного НЕ» можно использовать RS триггер. Только входы поменять местами, как на рис.50. Теперь подача импульса на вход приведет к появлению единичного состояния на выходе -Q. А на выходе Q появится состояние 0. Что соответствует противоположности и противопоставлению логической функции НЕ:
Результат в виде потенциала на выходе триггера останется и при прекращении действия условий на его входе. Это зафиксированный ответ логической задачи противопоставления. Для изменения результата надо изменить условие на входе. В данном случае, подать импульс на другой вход — «Установка». И элемент снова готов к работе. А как же смысл «НЕ» — исключение условия из результата операции?
Рис.51. Триггеры на логических элементах. Вот пример (рис.51. б) триггера на 3 устойчивых состояния. Он взят из публикаций А.П. Стахова [17 ]. Его работа соответствует смыслу «исключающего НЕ — ИЛИ» с фиксацией результата. Условие исключено, а на каком, из оставшихся выходов будет 1 – безразлично.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 1444. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 ; (2.11)
; (2.11) . (2.12)
. (2.12)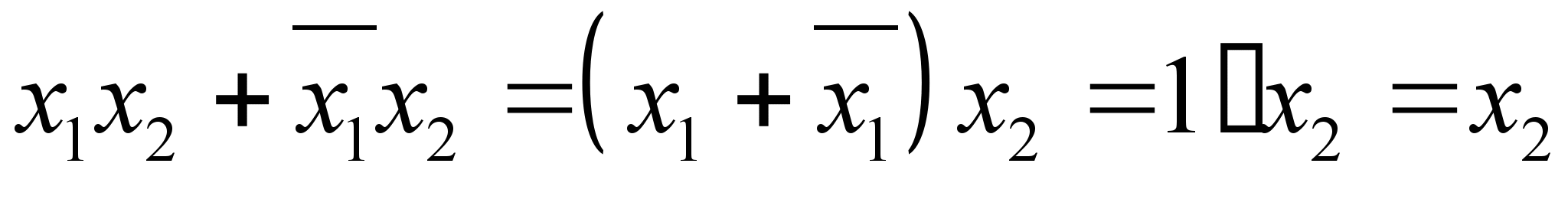 .
.
 (2.13)
(2.13) . (2.14)
. (2.14)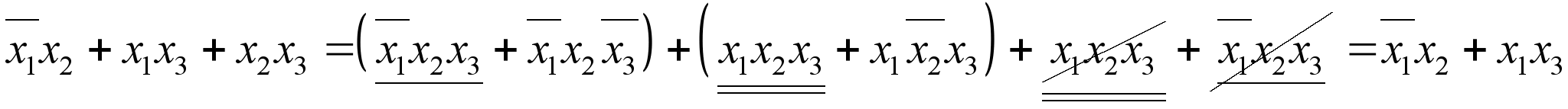
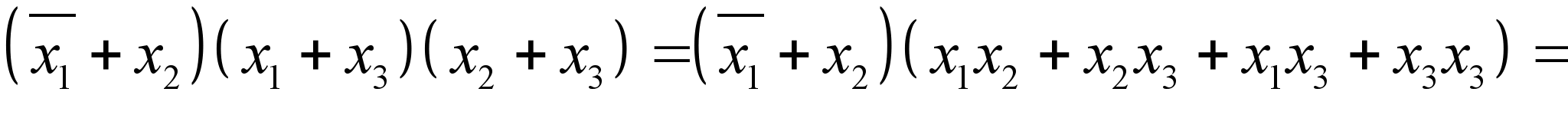
 ;
;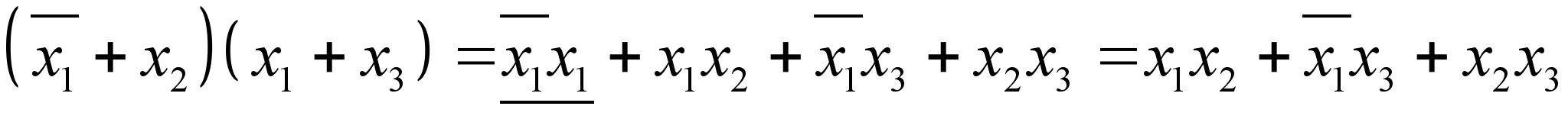 .
.





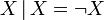 — отрицание
— отрицание — дизъюнкция
— дизъюнкция — конъюнкция
— конъюнкция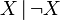 — константа 1
— константа 1

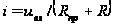 ,
, - прямое сопротивление диода.
- прямое сопротивление диода. .
.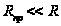 , тогда
, тогда 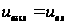 . При отрицательном входном напряжении ток идет через диод
. При отрицательном входном напряжении ток идет через диод ,
, - обратное сопротивление диода.
- обратное сопротивление диода. . Как правило,
. Как правило,  и
и  . При изменении полярности включения диода график функции
. При изменении полярности включения диода график функции  повернется на угол
повернется на угол 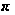 вокруг начала координат.
вокруг начала координат.
 не А
не А
