
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Индивидуальное многомерное шкалирование ⇐ ПредыдущаяСтр 8 из 8 Классическое многомерное шкалирование основано на предпосылке о том, что у всех респондентов существует единое пространство восприятия. В действительности же его может и не быть. Один из путей ослабления этой предпосылки - учет специфики метрик отдельных респондентов. Для этого проводится индивидуальное многомерное шкалирование. Аксиомы для расстояний в евклидовом пространстве:
Аксиомы для близостей (происходит смягчение требований):
Условия, налагаемые на элементы матрицы различий в метрическом МШ, строго соответствуют следующим аксиомам расстояния в геометрическом пространстве:  1) Аксиома о рефлексивности
подразумевает, что сравнительная оценка двух идентичных стимулов (i) не должна превышать оценки сравнения этого стимула с любым другим (j) в наборе. 2) Аксиома о симметричности
означает, что оценка различия стимулов i и j не должна зависеть от временных или пространственных перестановок этих стимулов относительно друг друга. 3) Аксиома треугольника
требует, чтобы сумма различия между стимулами i и j и различия между j и k в триаде стимулов i, j и k была не меньше, чем различие между оставшейся парой стимулов i и k. В терминах теории измерений выполнение этих аксиом означает, что субъективные оценки различий должны представлять собой величины на шкале отношений (Стивене, 1960). Только в этом случае их можно рассматривать как расстояния между точками в психологическом пространстве. При неметрическом МШ (Терехина, 19776; Шепард, 1981) исходная информация о различиях представляется в виде оценок, удовлетворяющих шкале порядка (Стивене, 1960). Конкретные числовые значения различий не учитываются. На соотношение субъективных различий и расстояний в психологическом пространстве в этом случае накладывается только требование монотонности. Иначе говоря, конфигурация точек-стимулов должна быть построена в пространстве мерностей таким образом, чтобы последовательности реконструируемых значений {d} и матричных величин {D} соответствовали друг другу по критерию сохранения взаимно однозначной монотонности (так называемому «стресс»-критерию). Конкретный вид соответствия {d} и {D} заранее не определяется и выступает как одно из неизвестных, находимых в процессе решения. 39. Основные модификации многомерного шкалирования: метрическое и неметрическое, индивидуальное, многомерное развертывание [3, 6, 7]. Как и в обычном многомерном шкалировании, основной целью неметрического многомерного шкалирования является представление объектов в пространстве восприятия, однако допускается, что различные респонденты по-разному воспринимают это пространство. Иначе говоря, оценка объектов респондентами происходит по одному и тому же набору базовых характеристик (пространству), но респонденты при оценке придают этим параметрам (осям) различные веса. Формально это означает, что при оценке близости между стимулами респонденты используют не обычное, а взвешенное расстояние. Говоря о методах метрического многомерного шкалирования, отметим только, что по типу отображения они делятся на линейные и нелинейные. Линейное метрическое шкалирование возникло первым, когда Торгерсон представил подробное описание алгоритма, начиная от процедуры сбора данных и кончая пространственным представлением30. Более поздние методы метрического многомерного шкалирования основаны на минимизации нелинейных функций несоответствия (критериев качества отображения) между исходными данными и пространственным представлением. В этом отношении они почти ничем не отличаются от методов неметрического многомерного шкалирования. Отличия этих методов заключены в самом виде функции несоответствия и объясняются различным уровнем измерения исходной информации. 40. Роль социолога в процессе применения многомерного шкалирования: формирование исходных данных и интерпретация результатов [3, 6, 7]. Шкала наименований(номинальная шкала) – шкала, при использовании которой для измерений получают минимальную информацию о сравниваемых объектах. А именно:
^ Шкала порядка наряду с информацией, предоставляемой шкалой наименований, обеспечивает получение дополнительной информации о ранжировании1 объектов, упорядоченных по возрастанию (убыванию) степени выраженности какой-либо их характеристики (предпочтительности, качества, затратам на производство). Наглядный пример – измерение температуры двух объектов без термометров: простым прикладыванием руки к поверхности определяют, у какого объекта температура выше (но при этом нельзя сказать, на сколько градусов выше). При измерении в такой шкале объекты могут быть ранжированы (упорядочены), например, по возрастанию температуры. Тогда получаемая в результате измерения информация будет выражаться в номере места каждого объекта в ранжированном ряду. ^ Шкала интервалов обладает еще большим информационным потенциалом. При измерении в этой шкале нескольких объектов, кроме информации, обеспечиваемой шкалой рангов, появляется дополнительная информация – на сколько один объект отличается от другого по измеряемой характеристике. Например, при измерении температуры шкалами интервалов используются шкалы Цельсия или Фаренгейта. При измерении в этих шкалах можно определить, на сколько градусов отличается температуры различных объектов, но нельзя узнать – во сколько раз объекты отличаются друг от друга по этой характеристике. Для этой шкалы функция, задающая отображение, имеет следующий вид:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 501. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , l=1, ... m
, l=1, ... m 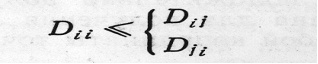
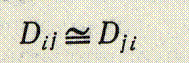
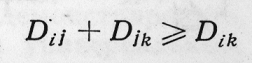
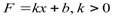 .
.