Геометрическая модель, «заложенная» в методе Терстоуна измерения установки.

Итак, нам надо понять, какова суть тех шкальных значений, которые мы хотим найти. Что мы, собственно, ищем?

Представление о мнении одного респондента об одном объекте

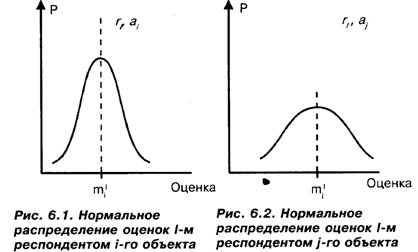
Начнем издалека. Зададимся вопросом о том, что из себя пред­ставляет мнение одного респондента об одном объекте.

Выше (в п. 5.2) мы говорили о том, что такое плюрализм мнения человека о каком-либо объекте. Вспомним соответству­ющее определение и будем считать, что мнение каждого рес­пондента о любом из шкалируемых нами объектов является плю­ралистичным. Ссылаясь на практику, мы отмечали, что конст­руктивно такое предположение может использоваться только в том случае, если оно формулируется строго, с использованием математического языка, и упоминали примеры такого рода фор­мулировок. Еще одним примером конструктивного подхода к определению интересующей нас плюралистичности и форми­рованию на его основе практических рекомендаций является модель Терстоуна парных сравнений. Опишем ее.

Предположим, что у нас имеются объекты α_μ а₂, а_п и рес­понденты г_р г₂, r_N. Предположим, что мнение одного респон­дента г, об одном объекте а. (1 — любое число из множества 1, 2,

N; i — любое число из множества 1, 2, п) представляет собой нормальное распределение (см. рис. 6.1).

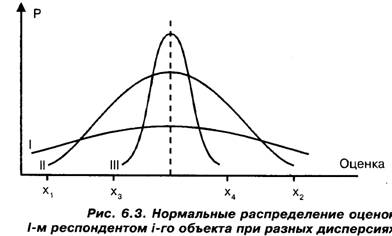
Проще говоря, это означает, что- при опросах, производя­щихся в разных условиях, наш "градусник" чаще всего будет показывать некоторую оценку т! (математическое ожидание, т.е. среднее значение нашего нормального распределения), реже — другие оценки. И чем дальше какое-либо число отстоит от т], тем реже оно будет встречаться в качестве такой оценки.

На рис. 6.2 изображено аналогичное распределение для того же респондента и другого объекта. Естественно, величины т! и т!, вообще говоря, будут различными, поскольку разные объек­ты респондент, вероятно, "в среднем" оценивает по-разному.

Вероятно, естественным выглядит предложение считать "ис­тинной" оценкой мнения нашего респондента о рассматривае­мом объекте соответствующее математическое ожидание. Оказы­вается, что и дисперсию рассматриваемых распределений мож­но проинтерпретировать естественным образом (напомним, что нормальное распределение однозначно задается значениями ма­тематического ожидания и дисперсии либо среднего квадрати-ческого отклонения). Покажем это.

Рассмотрим рис. 6.3, на котором изображены интересующие нас распределения, отвечающие разным дисперсиям.

Нетрудно понять, что дисперсия говорит о степени уверен­ности (убежденности) респондента в своем мнении о рассмат­риваемом объекте. Если это мнение определяется распределени­ем I, то респондент, будучи опрошенным в разное время, при­мерно с одинаковой вероятностью будет давать совершенно раз­личные ответы, в том числе и весьма отличающиеся от среднего. Так, значения x_i и х_г в его ответах могут встретиться почти с той же вероятностью, что и среднее значение.

Если мнение респондента определяется распределением III, то, напротив, значения, даже незначительно отличающиеся от среднего, такие, как х, и х₄, будут встречаться с гораздо меньшей вероятностью, чем само среднее. А вероятность получить от рес­пондента ответы χ_ί и х₂ будет практически равна 0.

При использовании распределения II ситуация будет зани­мать промежуточное положение между двумя описанными выше.

Ясно, что упомянутая степень уверенности может быть объяс­нена разными факторами: характером (принципиальностью)

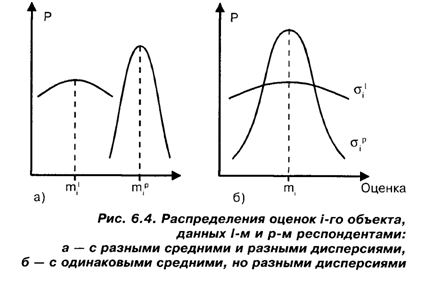
Пока будем считать, что дисперсии тех распределений, кото­рые отвечают мнениям одного респондента о разных объектах, вообще говоря, различны. Так, различны дисперсии распреде­лений, приведенных на рис. 6.1 и 6.2. Теперь перейдем к обсуж­дению вопроса: должны ли быть схожими, и, если должны, то в какой степени, распределения, отвечающие разным респон­дентам? Чтобы наша задача была осмысленна, и здесь (так же, как и в случае установочной шкалы Терстоуна) требуется опре­деленная однородность изучаемой совокупности респондентов.