Измерение вертикального угла. Понятие о МО вертикального угла.

Лимб жестко скреплен со зрительной трубой. Алидада всегда неподвижна.

Необходимые условия измерения:

1) визирная ось должна проходить через нулевой диаметр лимба (00-1800).

2) Ось уровня должна быть параллельна нулевому диаметру алидады.

Если эти условия выполнены, то при горизонтальном положении визирной оси отсчет по вертикальному кругу должен быть равен 0. Обычно эти условия немного нарушены, и отсчет отличается от нуля – «место нуля» (МО - отсчет по шкале вертикального круга, при котором визирная ось зрительной трубы горизонтальна, а пузырек уровня находится в нуль пункте)

Измерение угла наклона при КП.

ν- угол наклона между направлением визирной оси и ее горизонт проекцией, R- отсчет по лимбу при КП, М - наблюдаемая точка. ν=R-MO. При КЛ L-отсчет по лимбу при КЛ. ν=МО+(3600-L), ν=МО - L.

У различных типов теодолитов оцифровка вертикального круга не одинаковая. До начала измерений необходимо посмотреть оцифровку, а затем применять формулы. У Т-30- оцифровка от 00 до3600 против часовой стрелки. ν=(L-R-1800)/2, МО=(R+L+1800)/2, ν=MO-R-1800=L-MO.

Б18

Погрешности геодезических измерений. Свойства случайных погрешностей измерений.

Если принять какую-то в-ну за истинную X, измерив ее, получим результат измерения l. l-X=∆, ∆ - истинная ошибка погрешности измерения в общем случае рассматривают как сумму трех составляющих ее видов погрешности: грубой, систематической, случайной.

Ошибки бывают: элементарные (зависят от одного фактора), совокупные (несколько факторов), по происхождению, по причине.

Классификация ошибочных измерений:

1. Грубые ошибки, которые при заданных условиях измерений превышают установленный предел. Грубые ошибки – результат просчета. Их обнаруживают повторными измерениями и исключают.

2. Систематические ошибки, которые сохраняют свой знак и в-ну или изменяются по в-не в небольших пределах. Возникают из-за неправильной методики измерений, неисправности прибора, внешних условий. Их полностью исключить нельзя, можно уменьшить.

3.    Случайные ошибки, характер и влияние которых на каждое отдельное измерение остаются неизвестными.

Свойства случайных погрешностей:

- Случайная ошибка в заданных условиях измерения не может превышать установленного предела;

- Положительные и отрицательные ошибки равновозможны;

- Малые по абсолютн. в-не ошибки встречаются чаще, чем большие;

- Предел среднего арифметического из суммы случайной ошибки стремится к нулю, если число изм. m стремится к бесконечности.

Нивелирование. Методы нивелирования.

Нивелирование-изменение превышений.

-Геометрическое нивелирование - выполняется горизонтальным лучом визирования

-Тригонометрическое – выполняется наклонным лучом визирования.

-Физическое - основано на использовании различных физических явлений (барометр. нивелиров.,гидростатич.,гидродинамич.)

Б19

1. Критерии, используемые при оценке точности измерений.Оценка точности результатов равноточных измерений. Арифметическая середина

Если имеется ряд результатов равноточных измерений l1; l2; …; ln одной и той же величины, то за окончательное значение принимают среднюю арифметическую величину L из всех результатов.

.

Если истинное значение измеряемой величины х, то абсолютные ошибки будут равны:

Δ1= l1- х;

Δ2= l2- х;

………;

Δ n= ln- х,

________

[Δ] = [l] – nx.

Из суммы равенств получим, что .

В соответствии со свойством 4 случайных ошибок, с увеличением числа измерений величина при n → ∞.

Следовательно, при бесконечно большом числе измерений, среднее арифметическое L будет стремиться к истинному значению измеряемой величины х.

Величина при конечном числе измерений будет вероятнейшим значением определяемой величины, называемой арифметической серединой. Разность между результатом измерения и средним арифметическим называют уклонением от арифметической середины или вероятнейшими ошибками υ, т. е. l1 - L = υ1.

Сумма вероятнейших ошибок равняется нулю , если величина среднего арифметического не имела округлений.

В топографии и геодезии в качестве критериев точности измерений в основном применяют среднюю квадратическую ошибку и относительную ошибку.

Среднюю квадратическую ошибку отдельного результата измерения m вычисляют по формуле Гаусса: .

Формулу Гаусса можно использовать, когда известно истинное значе­ние измеренной величины, а для оценки точности величин, истинное значение которых неизвестно, применяется формула Бесселя , где υ – вероятнейшая ошибка.

Среднюю квадратическую ошибку арифметической середины М выражают через среднюю квадратическую ошибку m отдельного изме­рения, т. е. .

Таким образом, средняя квадратическая ошибка арифметической середины из результатов равноточных измерений в раз меньше средней квадратической ошибки результата отдельного измерения. Для уменьшения ошибки измерения, например, в 2 раза, количество измерений необходимо увеличить в 4 раза.

Применительно к конкретным условиям указывают критерий отбра­ковки результатов измерений. В качестве такого критерия служит пре­дельная ошибка. Для наиболее значимых измерений применяются повы­шенные требования к точности и величину предельной ошибки прини­мают равной 2m, т. е. Δпр.= 2m (удвоенное значение средней квадратической ошибки. Для менее значимых измерений принимается величина предельной ошибки равная 3m, т. е. Δпр.=3m (утроенное значение средней квадратической ошибки).

Пример, если при угловых измерениях m = 5˝, то «по правилу 2m» отбраковываются все результаты, значения которых по абсолютной величине больше 10˝, а применительно к «правилу 3m» отбраковываются – больше 15˝.

Для суждения о точности многих измерений недостаточно определения величины абсолютной ошибки, необходимо еще знать значение самой измеряемой величины. Так, для получения представления о точности линейных, площадных и других измерений применяется относительная ошибка.

Относительная ошибка – это отвлеченное число, выражающее отношение абсолютной ошибки к результату измерения. Относительную ошибку принято выражать простой дробью, числитель которой равен единице.

– для отдельного результата измерений

–для арифметической середины.

Значение знаменателя принято округлять до двух значимых цифр. Чем больше знаменатель, тем выше точность выполненных работ.

Рассмотрим пример. Измерены две линии: одна длиной 220 м со средней квадратической ошибкой 0,17 м, другая – длиной 390 м со средней квадратической ошибкой 0,23 м, т. е. L1 = 220 м, m1= 0,17 м, L2 = 390 м, m2=0,23 м. Какая из линий измерена точнее?

Подставив результаты измерений и вычислений в вышеприведенные формулы,получим,что относительная ошибка в первом случае будет равна , а во втором – . Следовательно, вторая линия измерена точнее, несмотря на большую величину абсолютной ошибки.

2. Определение недоступного расстояния.

Если препятствие (река, обрыв, здание) делает расстояние недоступным для измерения лентой, то его измеряют косвенным методом.

Так, для определения недоступного расстояния d измеряют лентой длину базиса b (рис. 8.3, а, б) и углы a и b . Из DABC находят

d = b sin a / sin (a + b),

где учтено, что sin g = sin (180°-a-b) = sin (a + b).

Для контроля расстояние d определяют ещё раз из треугольника ABC₁ и при отсутствии недопустимых расхождений вычисляют среднее.

Б20

1. Равноточные измерения. Понятие об арифметической середине.

Равноточные – это результаты измерений однородных величин, выполняемые с помощью приборов одного класса, одним и тем же методом, одним исполнителем при одних и тех же условиях. Все остальные измерения относятся к неравноточным. Арифметическая середина. Пусть имеется n измерений одной величины X, то-есть,

(1.34)

Сложим эти равенства, суммарное уравнение разделим на n и получим:

(1.35)

Величина (1.36)

называется средним арифметическим или простой арифметической серединой

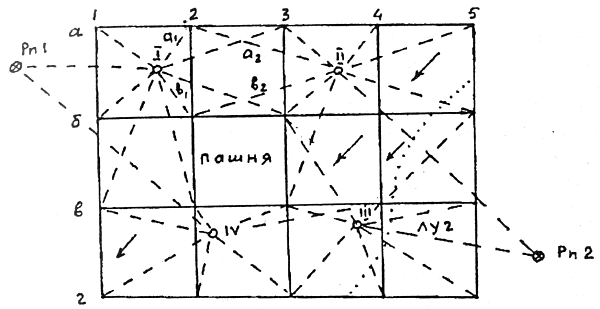
2. Нивелирование поверхности как метод съемки.

Нивелирование поверхности — один из способов топографической съемки, при котором на местности по определенному правилу располагают точки, высоты которых определяют геометрическим нивелированием. Наибольшее практическое применение имеет метод квадратов и метод магистралей с поперечными профилями. Создание плана по результатам нивелирования по квадратам начинают с разбивки в заданном масштабе сетки квадратов, у каждой выписывают округленную до сантиметра высоту. Согласно абрису наносят и вычерчивают в условных знаках ситуацию, а затем путем интерполирования горизонталями изображают рельеф.
Топографическую съемку небольших участков равнинной местности с небольшим количеством контуров при высоте сечения рельефа через 0,1; 0,25; 0,5 м выполняют нивелированием поверхности по квадратам, прямоугольникам, характерным линиям рельефа и т. п. Отметки пикетов во всех способа определяют точек.
При нивелировании по квадратам геометрическим нивелированием, различие состоит в методе определения планового положения и мерным прибором на местности разбивают сетку квадратов, в вершинах квадратов забивают колышки. Сначала строят квадраты со сторонами 100, 200 или 400 м, а затем получая более мелкие квадраты со сторонами 40 м при съемке в масштабе 1:2000, 20 м — при съемке в масштабе 1:1000 и 1:500. При разбивке квадратов выполняют съемку ситуации. Результаты съемки фиксируют в абрисе (рис. 1).

Рис. 1. Абрис нивелирования поверхности по квадратам (стрелками показано направление скатов).

Нивелир устанавливают так, чтобы с меньшего количества станций выполнить съемку всего участка. Установив нивелир на станции I, берут отсчет по рейке, поставленной на опорной высотной точке (например на Рп I) и вычисляют:

ГП = Нрn + а,
где Нрn — отметка репера; а — отсчет по рейке, установленной на репере. У номеров вершин квадратов выписывают отсчеты по рейкам, установленным на них, в абрисе штриховыми линиями показывают, на какие вершины квадратов выполнено нивелирование с данной станции. Отметки вершин квадратов вычисляют по формуле:
Нi = ГП - а
Подобным образом выполняют нивелирование и с других станций с обязательным определением ГП на каждой станции по опорным высотным пунктам или связующим точкам. С каждой последующей станции нивелируют несколько связующих точек, при этом (см. рис. 1.27) а1+ b2 = а2 + b1, расхождение между этими суммами не должно превышать 10 мм.
Нивелирование по параллельным линиям.
При нивелировании по параллельным линиям прокладывают параллельные магистральные ходы, часто по характерным линиям рельефа, по обе стороны от каждого хода разбивают перпендикулярные линии (поперечники). По ходам и поперечникам через 40 м при съемке в масштабе 1:2000 и 20 м — при съемке в масштабах 1:1000 и 1:500 закрепляют пикеты и снимают ситуацию. Высоты пикетов определяют геометрическим нивелированием.
Разбивка и нивелирование поверхности по квадратам полярным способом.
Для разработки проектов вертикальной планировки традиционно применяется способ нивелирования поверхности по квадратам. На первом этапе на местности выполняют построение сетки квадратов при помощи теодолита и мерной ленты. На границе участка строят прямоугольник (или квадрат), на сторонах которого закрепляют вершины квадратов через заданные интервалы, а положение вершин в середине участка находят на пересечении створов, проходящих через соответствующие вершины на внешней границе. Все вершины заполняющих квадратов закрепляют кольями. На втором этапе выполняют геометрическое нивелирование вершин
квадратов.
Первоначальная разбивка, как правило, служит только для выполнения съемки: до начала строительных работ проходит значительный период времени, разбивка частично или полностью утрачивается и требует восстановления.
Методика предусматривает долговременное закрепление только двух основных взаимно перпендикулярных осей площадки. Положение вершин квадратов определяется полярным способом. За исходную ось полярных координат может быть принята одна из основных закрепленных осей, а в качестве полюса – пересечение осей.

Для сравнения результатов с результатами, приведенными в [1], на местности выбрана открытая площадка со спокойным рельефом размером 80 × 80 м. Измерения выполнены теодолитом 2Т30П с уровнем при зрительной трубе и рейкой РН-3. После разбивки и закрепления основных осей за полярную была принята ось 3 – 3, за полюс 0 – центр площадки. На рис. 1 приведена схема разбивки сетки квадратов полярным способом.

Значения полярных углов и расстояний, соответствующих сетке квадратов со сторонами 20 м, вычислены заранее (до производства работ) и записаны на схеме в вершинах квадратов.

На местности расстояния от полюса до вершин квадратов определялись нитяным дальномером теодолита с отсчетами по рейке до десятых долей сантиметра. Для определения положения вершин по каждому направлению визирования выставлялась веха за пределами границы площадки. Рабочий - реечник, двигаясь от теодолита к вехе шагами, отсчитывал расстояние до искомой вершины и устанавливал рейку. Отметим, что перед началом работы реечнику необходимо определить среднюю длину шага и запомнить число шагов, соответствующее длине стороны и диагонали квадрата. Приблизительное определение сравнительно небольших расстояний (в нашем случае до 60 м) парами шагов является известным примером в геодезических работах. Наблюдатель у теодолита корректировал положение рейки по линии визирования и определял дальномерное расстояние до нее. Если измеренное расстояние отличалось от теоретического значения более чем на ±0,5 м, положение рейки вновь корректировалось по расстоянию и створу. Практика показала, что требуемая точность достигается за одно-два приближения. Одновременно с окончательным определением планового положения наблюдатель выполнял нивелирование вершины квадрата. Рельеф местности позволил выполнить высотную съемку всех вершин при горизонтальном положении визирной оси зрительной трубы. Однако в общем случае (при больших уклонах местности и превышениях) требуется тригонометрическое нивелирование.
Последовательность определения положения и нивелирования вершин была следующей: первоначально взяты вершины по направлениям диагоналей площадки Г/4, Д/5; Б/4, А/5; Б/2, А/1; Г/2, Д/1, при этом угловые
точки площадки Д/5, А/5, А/1 и Д/1 были закреплены. Затем последовательно, начиная с точек на полярной оси
(О – Д/3), были определены положения и высотные отметки остальных вершин квадратов. Положение вершин на границах площадки дополнительно контролировалось визуально по створам между угловыми точками. Ра-
бота выполнена бригадой в составе четырех человек. На рис. 2 приведена схема высотных отметок в вершинах квадратов.
На схеме записаны значения отметок, которые определены изложенным способом, и ниже – традиционным способом. Вычислены расхождения в значениях отметок.
Рис. 2 Схема высотных отметок в вершинах квадратов
Среднее квадратическое расхождение по высотным отметкам составило 1,9 см, по положению вершин вплане – 0,15 м (для сравнения – в работе [1] соответственно 1,4 см и 0,12 м). Такие погрешности вполне допустимы при изображении рельефа на топоплане.
В заключение отметим, что условия открытой местности позволили выполнить съемку с одной станции
(полюса). В данных условиях разбивка и нивелирование сетки квадратов полярным способом по затратам вре-мени оказались экономичнее традиционного способа на 35 %.
Полученные результаты подтверждают возможность эффективного применения полярного способа при составлении проектов вертикальной планировки и определении объемов земляных работ.

Б21

1. Оценка качества функций измеренных величин. Впрактике геод работ часто возникает необходимость найти среднюю квадратическую ошибку функции, если известны средние квадратические ошибки её аргументов, и наоборот. Рассмотрим функцию общего вида F= f (x y z …. U) дге x y z — независимые аргументы, полученные из наблюдений со средними квадратическими ошибками mx my mz соответственно. Из теории ошибок измерений известно что средняя квадратическая ошибка функции независимых аргументов равна корню квадратному из суммы квадратов произведений частных производных функций по каждому из аргументов на средние квадратические ошибки соответствующих аргументов m_x².

2. Методы топографических съемок.

Виды методы и способы топографических съемок, используемых при создании топографических карт
Основным процессом создания топографической карты является топографическая съемка (или составление). Топографическая съемка – это комплекс работ с целью создания съемочного (составительского) оригинала карты.
Топографическая съемка, при которой все измерения, необходимые для создания съемочного оригинала карты, выполняются непосредственно на местности, называется мензульной топографической съемкой.
Теорией и практикой создания карт по фотоснимкам занимается раздел фотограмметрии – фототопография.
Топографические съемки с применением фотоснимков называются фототопографическими. Обычно фототопографическая съемка включает три этапа:
фотографирование местности;
полевые работы;
камеральные работы.
В зависимости от места, откуда выполняется фотографирование, различают следующие в и д ы фототопографических съемок:
наземная фототопографическая;
аэрофототопографическая;
комбинированная фототопографическая и
космическая фототопографическая.

Наземная фототопографическая съемка основана на приме- нении наземных (фототеодолитных) фотоснимков. Фотографирование производится с точек земной поверхности специальным прибором – фототеодолитом. Поэтому съемку называют еще фототеодолитной.
При аэрофототопографической съемке (АФТС) фотографирование местности производится с самолета или любого другого летательного аппарата, перемещающегося в воздушном пространстве.
Если при создании съемочного оригинала карты сочетается наземная и аэрофототопографическая съемки, то такая съемка называется комбинированной фототопографической съемкой.
Снимки, полученные из космоса, составляют основной исходный материал для космической фототопографической съемки.

Б22

1. Линейные измерения. Принцип измерения длин линий. Прямые и косвенные измерения.

Косвенный способ измерения расстояний.

Измерение расстояния с помощью дальномеров. Различают дальномеры: оптические, светодальномеры и радиодальномеры. Принцип измерение расстояния сводится к решению треугольника, в котором по малому углу β и противолежащей стороне (базису) b нужно вычислить расстояние D. D=b*ctgβ

Различают дальномеры: с постоянным углом и переменным базисом, с постоянным базисом и переменным углом. Представителем оптич дальномера с пост углом явл нитяной дальномер.

В поле зрения трубы теодолита имеются дополнительные штрихи (дальномерные); они позволяют с помощью рейки с делениями измерить расстояние от теодолита до рейки.