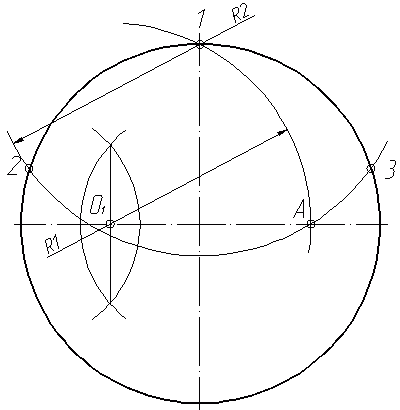ЗАДАНИЕ 103. Пирамида с вырезом (формат А3)

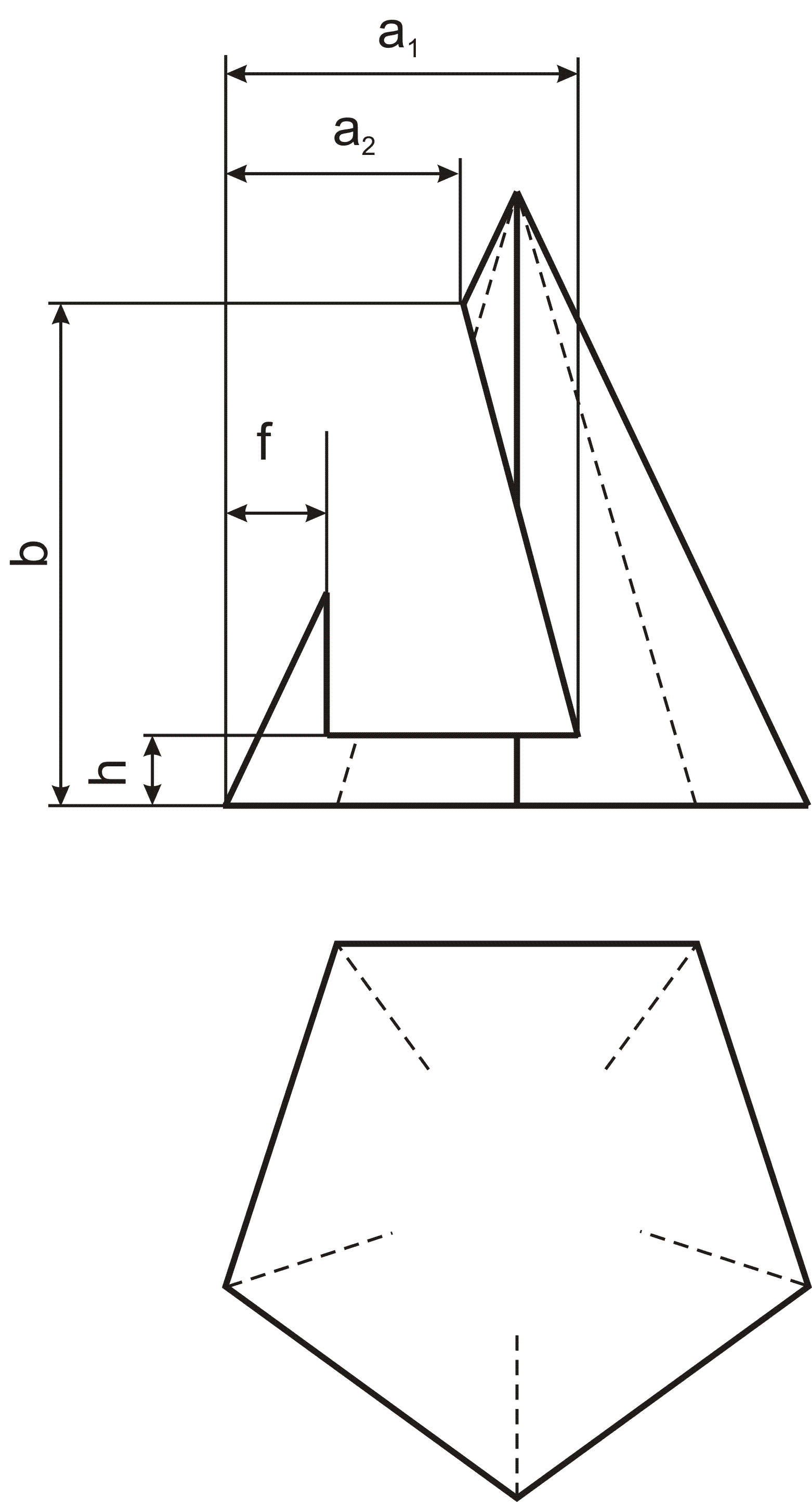
Задание выполняется на формате А3 (формат располагается горизонтально).

Масштаб-1:1

Задание: По главному изображению пирамиды, рассеченного проецирующими плоскостями, выполнить построение двух остальных видов. Выполнить проекции линий разреза на остальных видах.

В задании предъявлено главное изображение пирамиды. Варианты заданий для листа 103 имеют, примерно, вид, указанный на рис.10. Основание пирамиды вписано в окружность диаметром 100 мм. Высота пирамиды 100 мм. Остальные исходные данные по вариантам приведены в таблице.

Рис.10 . Пример задания 103

Задача 1. Построение двух видов пирамиды по заданному главному изображению.

Вначале строится вид сверху (правильный пятиугольник). Затем выполняется построение главного вида и вида слева. При этом возникает необходимость найти проекции точек основания.

Задача 2. Построение проекций выреза на этих видах.

Построение проекций выреза сводится к последовательному трехкратному решению задачи пересечения пирамиды плоскостью.

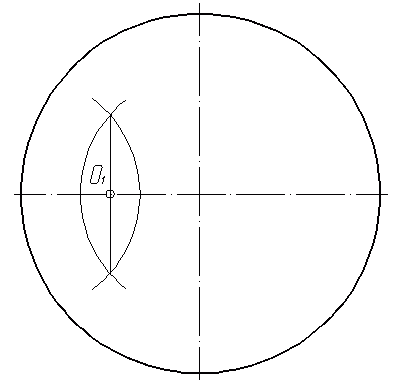
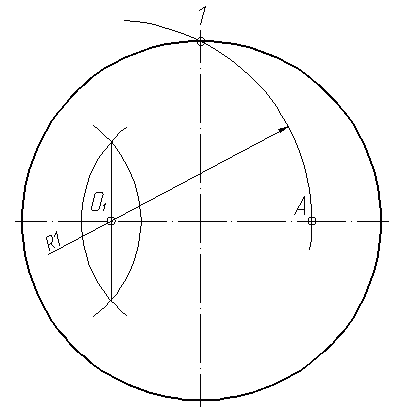
Справочные материалы к заданию 103

Деление окружности на 5 частей.

Деление окружности на пять частей выглядит более путанным, чем деление окружности на привычные 6 частей. Но на самом деле, и это построение не вызовет у вас сложности, если вы будете знать алгоритм.

Чтобы разделить окружность на 5 равных частей, нужно выполнить следующие шаги:

Для начала построим точку О1. Она лежит на горизонтальной оси на расстоянии полурадиуса от центра. Для нахождения середины отрезка используется метод засечек (рис.11).

Начнем построение пятиугольника. Проведем дугу радиусом R1 с центром в точке О1, проходящую через точку 1. Получим точку А (рис.12).

                       Рис.11                                         Рис.12

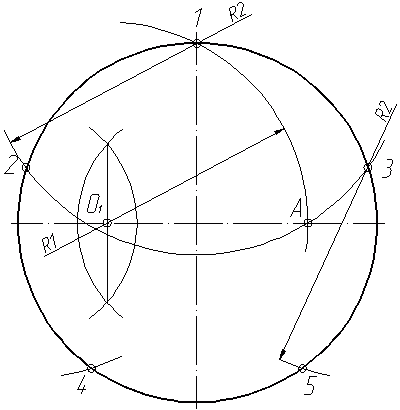
Теперь проведем дугу радиусом R2 с центром в точке 1 и проходящую через точку А. Мы получили точки 2 и 3 (рис.13)..

Из точек 2 и 3 таким же радиусом R2 сделаем еще две засечки на окружности - точки 4 и 5. Таким образом, мы получил пять точек, делящих окружность на 5 равных частей (рис.14).

                       Рис.13                                         Рис.14

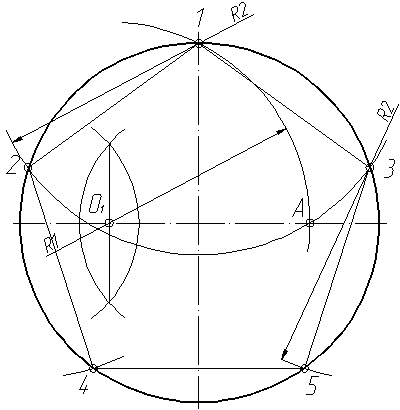
Для наглядности соединим полученные точки между собой - получим правильный пятиугольник (рис.15).

                                          Рис.15

Запомнив этот алгоритм вы всегда сможете при необходимости разделить окружность на 5 равных частей. или же построить правильный пятиугольник.

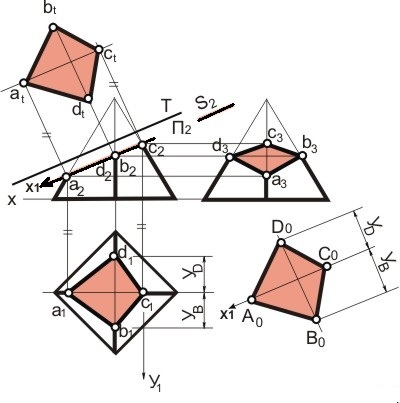
Пересечение многогранников плоскостью.

Пример конструирования устойчивой подставки в виде усеченной пирамиды показан на рис.16.4. Наклонная площадка ABCD образована срезом верхней части пирамиды фронтально- проецирующей плоскостью S (S₂). Фронтальные проекции a₂, b₂, c₂, d₂ точек находятся на фронтальном следе S₂ плоскости, а фронтальная проекция площадки ABCD совпадает со следом S₂. Профильная a₃b₃c₃d₃ и горизонтальная a₁b₁c₁d₁проекции площадки построены по проекциям указанных точек на проекциях соответствующих ребер.

Рис.16