Сопряжение двух дуг окружностей третьей дугой

При построении сопряжения двух дуг окружностей третьей дугой заданного радиуса можно рассмотреть три случая: когда сопрягающая дуга радиусаR касается заданных дуг радиусов R1 и R2 с внешней стороны (рис. 6, а); когда она создает внутреннее касание (рис. 6, б); когда сочетаются внутреннее и внешнее касания (рис. 6, в).

Построение центра О сопрягающей дуги радиуса R при внешнем касании осуществляется в следующем порядке: из центра О1 радиусом, равным R + R1,проводят вспомогательную дугу, а из центра O2 проводят вспомогательную дугу радиусом R + R2. На пересечении дуг получают центр О сопрягаемой дуги радиуса R, а на пересечении радиусом R + R1и R + R2 с дугами окружностей получают точки сопряжения А и А1.

Построение центра О при внутреннем касании отличается тем, что из центра О1 проводят вспомогательную окружность радиусом, равным R — R1 а из центра О2 радиусом R — R2. При сочетании внутреннего и внешнего касания из центра О1 проводят вспомогательную окружность радиусом, равным R —R1, а из центра О2 — радиусом, равным R + R2.

Сопряжение дуги окружности и прямой линии второй дугой

Здесь может быть рассмотрено два случая: внешнее сопряжение (рис. 35, а) и внутреннее (рис. 35, б). В том и в другом случае при построении сопрягающей дуги радиуса R центр сопряжения О лежит на пересечении геометрических мест точек, равно удаленных от прямой и дуги радиуса R на величину R1.

При построении внешнего сопряжения параллельно заданной прямой на расстоянии R1 в сторону окружности проводят вспомогательную прямую, а из центра О радиусом,равным R + R1,— вспомогательную окружность, и на их пересечении получают точку О1 — центр сопрягающей окружности. Из этого центра радиусом R проводят сопрягающую дугу между точками А и А1, построение которых видно из чертежа.

Построение внутреннего сопряжения отличается тем, что из центра О проводят вспомогательную дугу радиусом, равным R — R1.

Рис. 6. Сопряжение двух дуг окружностей третьей дугой

Рис. 7. Сопряжение дуги окружности и прямой линии второй дугой

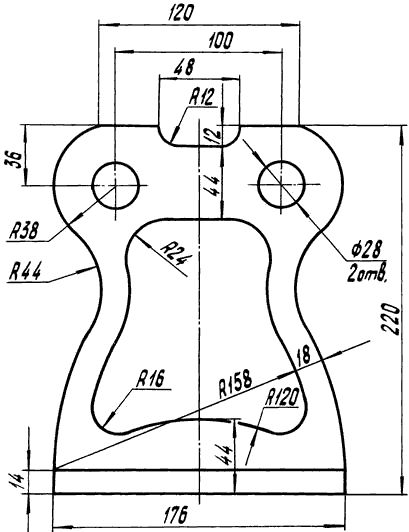
Варианты задания 101

1	2
3	4
5	6
7	8
9	10
11	12

ЗАДАНИЕ 102. Построение лекальных кривых

Задание выполняется на формате А3 (формат располагается горизонтально).

Масштаб-1:1.

Цель работы: Изучение типов линий и приобретение навыков их выполнения (ГОСТ 2.303-68). Изучение построений лекальных кривых по характерным точкам. Изучение приемов написания букв и цифр чертежным шрифтом (ГОСТ 2.304-81).

Задание: Построить изображение эллипса.

Методика оформления и последовательность выполнения задания «Построение лекальных кривых»:

1. Подготовить формат А3. Нанести внутреннюю рамку и прямоугольник основной надписи (185 x 55).

2. Провести горизонтальную прямую. Отметить на ней точку О и  построить в точке О сопряжённые диаметры эллипса KL и ЕМ: больший—под углом a ° к горизонтальной прямой, малый — под углом b °(рис.8).

Рис.8                                                             Рис9

3. Проведя через концевые точки К и L, E и M прямые, параллельные осям, получить параллелограмм

4. Поделить большую сторону параллелограмма и малую ось на равное число частей, например на восемь.

5. Из точек К и L через точки деления провести лучи; пересечения лучей дают точки эллипса. °(рис.9).

6. Сделать обводку чертежа с помощью лекал.

7. Заполнить основную надпись.

Исходные данные к заданию 102