
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Формирование дележа в форме вектора Шепли ⇐ ПредыдущаяСтр 2 из 2 5.3.1. Анализ общего выражения вектора Шепли [199] Условия оптимальности дележа на основе С-ядра и Н–М-решений и других близких к ним подходов являются плохо обусловленными в условиях невыпуклости и некомпактности обсуждаемых множеств и трудно реализуемыми даже при наличии наилучших свойств множеств. Поэтому [199] имеет смысл поставить вопрос о заранее ожидаемом определённом значении выигрыша каждого игрока. Оказывается, что некоторое априорно ожидаемое значение можно найти. Пусть p – любая перестановка множества Все перестановки равновероятны, т.е. имеют вероятность 1/N! каждая. Множество первых i игроков по порождённому перестановкой p порядку обозначим через Когда игрок i входит в коалицию p(i)-м по порядку, то множество первых p(i) игроков равно Общий выигрыш коалиции После вступления в коалицию i-го игрока равновесный выигрыш соответственно равен Тогда разность Для пояснения изложенного рассмотрим пример:

Определение 5.9.Игрок i в кооперативной игре называется болваном, если То есть игрок i не привносит в коалицию ничего по сравнению с тем, что он имел бы, если бы действовал самостоятельно. Определение 5.10. Коалиция, содержащая всех игроков, не являющихся болванами, R = {iÎN: называется носителем игры. Определение 5.11.Если R – носитель игры, а K – любая коалиция где Так как игроки вступают в коалицию в любом порядке, то можно сформировать «априорно ожидаемый выигрыш» игрока i как усредненную по всем перестановкам «долю» игрока i [152, 119] Определение 5.12. Вектор Ф( называется вектором Шепли. В соответствии с примером:
Таким образом, при малом N вектор Шепли можно получить непосредственно из общего выражения (5.17). 5.3.2. Свойства вектора дележа Шепли Свойство 5.1.Основным свойством по определению является то, что Фi( Свойство 5.2 [42, 152, 199]. Для всякой характеристической функции A1. Если R – носитель игры, то Эта аксиома означает, что из общего выигрыша коалиции R выделяется дополнительно «болвану» – или на «болванов» ничего не выделяется из общественных средств и не взимается с них. А2. Для любой перестановки p такой, что где K = (i1…iK), p(K) = (p(i1)…p(iK)), Фi( То есть игроки, одинаково входящие в коалицию, получают одинаковый выигрыш – или [152] игроки при переименовании получают те же значения выигрыша (выигрыш не зависит от обозначений). А3. Если Фi ( где ( Это означает, что при участии игрока в двух играх выигрыши отдельных игр складываются. Свойство 5.3[199]. Для любой характеристической функции вектор Шепли является дележом. Доказательство. На основании равенства (5.16) при K = N
То есть Условие коллективного рационального дележа выполнено. Раскроем выражение (17)
где Ki – все возможные коалиции, содержащие i-го игрока. Тогда, применяя свойство супераддитивности функции
получим Условие индивидуальной рациональности дележа также выполнено. Следовательно, Ф( Свойство 5.4. Для того чтобы вектор Шепли принадлежал С-ядру, необходимо и достаточно, чтобы для любого K Ì N он удовлетворял условию Действительно, так как вектор Шепли является дележом, для него справедливы все утверждения для дележей. Напомним, что С-ядро существует, если K и Фi – выпуклые ограниченные множества и функции соответственно. Свойство 5.5.Так как вектор Шепли – делёж, то по утверждению 5.4 вектор Шепли либо находится на Парето-границе П–Н-множества компромиссных решений игры N лиц, либо проектируется на Парето-множество в виде предпосылки дележа и даёт оценку эффективности i-го объекта – игрока на множестве возможных коалиций с другими объектами ММС (в утверждении 5.10 это показано для любой 5.3.3. Вычисление вектора Шепли Рассмотрим способ компактного вычисления вектора Шепли. Для этого фиксируем KÌN и вводим обозначение s = |K|, где |K| – «мощность» множества K (число элементов). Пусть где суммирование ведётся по всем K, содержащим i-го игрока. Пусть перестановка pÎQ. Представим её как В соотношении (5.22) надо вычислить |W|. Это число всевозможных перестановок p, таких что
Очевидно, что для множества cледовательно |W| = (s – 1)!(N – s)!. Подставляя это выражение в формулу (5.22), получаем формулу, удобную для вычисления вектора Шепли: где суммирование происходит по всем коалициям K, содержащим i-го игрока. Приведём несколько вариантов решения в зависимости от N. При N = 2
При N = 3 возможные коалиции K с игроком i i = 1: (1,2,3);(1,2);(1,3);(1), i = 2: (1,2,3);(1,2);(2,3);(2), i = 3: (1,2,3);(1,3);(3,2);(3). Поэтому, например (сравнить с (5.18а)), Утверждение 5.8. Численные значения компонент {Фi, iÎN} вектора дележа Шепли являются линейными комбинациями показателей конечного числа R-задач Парето- и Нэш-оптимизации, причём R удовлетворяет следующему соотношению: RN+1 = 2RN, при R2 = 2. В конечном наборе RN при каждом фиксированном Утверждение 5.9. При N = 2 в игре с постоянной суммой с характеристической функцией (5.3) вектор Шепли – обобщение максиминной цены. Доказательство. Имеем J1+J2 = 0;
При наличии равновесия
Тогда из (5.24) имеем
Следовательно, вектор Шепли есть обобщение максиминной цены. Если равновесие отсутствует, то
Следовательно, вектор Шепли соответствует гарантирующей игре с нулевой суммой Ф1+Ф2 = 0. Утверждение 5.10. Вектор Шепли при общих свойствах Парето-множества и при любой характеристической функции обеспечивает на Парето-границе ПНОК (Парето–Нэш-области компромиссов) сильную предпосылку дележа игры из условий: для задачи максимизации для задачи минимизации Рассмотрим метод вычисления вектора Шепли. Общая формула вычисления вектора Шепли имеет вид (5.23). Без ограничения общности рассуждений рассмотрим вариант (5.26б) для случая N = 2. Тогда формула вычисления вектора Шепли принимают вид (5.24), где Решим систему уравнений: При замене 2Ф1 = 2Ф2 = Вычтем из уравнения (5.28) уравнение (5.27): 2(Ф2 – Ф1) = 2( Ф2 – Ф1 = Ф2 и Ф1 – координаты точки Шепли, Из (5.29) следует, что точка Шепли и точка Нэша являются диагонально противоположными вершинами квадрата. Точка Шепли всегда лежит на линии, проведённой из точки Нэша под углом 45° к оси 0J1 (линия с наклоном +1; J2 = J1+b; b = const). Эту линию назовем линией равных выигрышей (см. рис. 5.1). Сложим уравнения (5.27) и (5.28): 2(Ф2 + Ф1) = 2( Ф2 + Ф1 = Ф2 и Ф1 – координаты точки Шепли, Из (5.30) следует, что точка Шепли и точка min( Точка Шепли лежит на пересечении линии, проведённой из точки Нэша с наклоном +1 (угол 45° к оси 0J1) (линия равных выигрышей) с линией, проведённой из точки min( Так как точка min( В частном случае точка Шепли может принадлежать Парето-множеству в трёх случаях: · точка min( · Парето-граница представляет собой прямую линию, составляющую с осью 0J1 угол 1350, т.е. с наклоном –1; тогда вся Парето-граница состоит из точек min( · Парето-граница имеет такую форму, что имеется несколько точек min( Во всех рассмотренных трёх случаях, если точка Шепли является точкой min(
Рис. 5.1. Геометрическая интерпретация получения точки Шепли при N = 2 В общем случае имеем следующие соотношения: точка Нэша – равновесная точка, которая обладает свойствами устойчивости (стабильности); точка min( точка Шепли – «априорно ожидаемое значение» – значение выигрыша каждого игрока, усреднённое по всем перестановкам, по всем возможным коалициям. Точка Шепли является способом оценки полезности возможного вступления в коалиционные связи. Утверждение 5.10 может быть обобщено на случай N ³ 3. 5.4. формирование двухэтапного метода оптимизации решений Получение значений вектора Шепли позволяет сделать вывод о полезности кооперативного компромисса для объектов ММС. Следующей задачей становится выбор способа объединения объектов в кооперацию, реализующую выявленную дополнительную эффективность. В общем случае основным является подход, связанный с объединением ресурсов, перестройкой оптимизационной структуры управления ММС, созданием новых технических средств поддержки и др. Ориентировкой реализации управляющих функций и параметров ММС в этом общем случае и вариантом реализации кооперативного компромисса при наличии практической полезной и мало меняющейся «при входе» в кооперацию математической модели ММС может служить выбор управлений и параметров состояний ММС, которые обеспечивают близость показателей цели ММС к полученным значениям вектора Шепли. В таком случае может быть сформирован алгоритм оптимизации решений, состоящий из следующих двух этапов. Этап 1.Определение значений вектора дележа Шепли {Фi, iÎN} на основе выражений (5.23), которые для N = 2,3 приведены в (5.24), (5.25). Если при решении задачи этапа 1 применяются (5.1), (5.3), то данный набор задач может быть решён с помощью ПС «MOMДИС» (см. гл. 9), в составе которой реализованы модули Парето- и Нэш- оптимизации. При неединственности вектора Шепли, вызванной возможной неединственностью решения задач Парето–Нэш-оптимизации, в качестве дополнительного подэтапа возникает задача определения дополнительного компромисса на основе групповой неудовлетворённости (см. гл.6 – частный случай СТЭК-14 (6.53)). Теперь Ф*Î{Ф} выбирается из условия где J* = {
Рис. 5.2. Структурная схема двухэтапного метода параметрической оптимизации управления ММС на основе вектора дележа Шепли Этап 2. Целью данного этапа является решение относительно управлений системы функциональных уравнений Данная система может быть приведена к обычной форме задачи оптимизации. С учётом параметризации ПКЗУ и параметрическим уточнением кооперативной структуры ММС задача оптимизации принимает вид Для решения задачи определения параметризованного программного управления и ПКЗУ применяется модуль W-оптимизации ПС «МОМДИС». На рис. 5.2 дана структурная схема двухэтапного алгоритма Шепли-оптимизации ММС.
Постановка данной задачи подобна постановке рассмотренной в 4.5.1. Структура взаимодействия в ММС совпадает со структурной схемой на рис. 4.5. Описание модели дается выражениями (4.47), (4.48). Показатели описываются формулами (4.49). Вариант прогноза также упрощенный, полное исследование дано в главе 10. В отличие от 4.5.1 рассматривается двухтактный прогноз с получением аппроксимированного программного управления, который при повторении двухтактного прогноза на следующем временном интервале позволяет получить ПКЗУ. Кроме того, как показано ниже, данный пример реализует стабильно-эффективный компромисс на основе Парето–Нэш–УКУ–Шепли-комбинации (СТЭК-7, см. главу 6). За основу взят аналогичный базовый вариант условий и начальных значений. Далее приводятся результаты оптимизации на основе двухэтапного алгоритма при двухтактном прогнозе (0,Т/2,Т). Первый такт прогноза: 1. Определение значений вектора дележа Шепли на основе Парето–Нэш-оптимизации (первый этап алгоритма). Общий вид множества показателей J1, J2 на основе ортогональной и ЛП-сетей дан на рис. 5.3. УКУ, Парето-граница, точки Нэша и Шепли даны на рис. 5.4: · точка min(J1+J2): q1 = 1; q2 = 0; J1 = – 38,7; J2 = - 40,4; · точка Нэша: q1r = 0,668; q2r = 0,430; J1r = – 10,2; J2r = – 7,29; · точка Шепли: Ф1 = – 41,005; Ф2 = – 38,095 (в соответствии с (5.24)).
Рис. 5.3. Множество показателей J1, J2 (на сетевой основе)
Рис. 5.4. Результаты первого этапа алгоритма 2. Векторная оптимизация управления коалициями для минимизации отклонения от точки Шепли (на основе W-оптимизации) (второй этап алгоритма) на множестве показателей Точки Парето, Нэша и Шепли, полученные на первом этапе, в данной системе координат принимают следующие значения: · точка · точка Нэша · точка Шепли Результатом оптимизации является точка сильной предпосылки игры и УКУ (СТЭК при однотактовом прогнозе) (рис. 5.5):
Таким образом, Парето–УКУ–Шепли-оптимальный вектор параметров на первом такте:
 
Рис. 5.5. Результаты второго этапа алгоритма на первом такте прогноза
Рис. 5.6. СТЭК при однотактовом прогнозе (окрестность начала координат (рис. 5.5)) Вектор состояния к концу первого такта: x1 = 9,972; x2 = 2,027; Второй такт прогноза:
|
 , т.е. преобразование каждого игрока i в p(i). Всего таких преобразований N!, где N – число элементов множества. Пусть игроки образуют одну коалицию, вступая в неё по одному в произвольном порядке, т.е. порядок вступления в коалицию случаен. Следовательно, игроки упорядочиваются согласно некоторой случайной перестановке p : N ® N.
, т.е. преобразование каждого игрока i в p(i). Всего таких преобразований N!, где N – число элементов множества. Пусть игроки образуют одну коалицию, вступая в неё по одному в произвольном порядке, т.е. порядок вступления в коалицию случаен. Следовательно, игроки упорядочиваются согласно некоторой случайной перестановке p : N ® N.
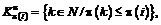 а множество игроков, вступивших в коалицию до него, имеет вид
а множество игроков, вступивших в коалицию до него, имеет вид \(i) = {kÎN| p(k) < p(i)}.
\(i) = {kÎN| p(k) < p(i)}. (
(  .
. ;
;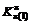 = (1);(1); (2,1); (2,3,1), (3,1), (3,2,1) = (1); (2,1);(3,1);(2,3,1);
= (1);(1); (2,1); (2,3,1), (3,1), (3,2,1) = (1); (2,1);(3,1);(2,3,1); = (1,2); (1,3,2); (2), (2), (3,1,2)(3,2) = (1,2); (1,3,2);(2);(3,2) и т.д.;
= (1,2); (1,3,2); (2), (2), (3,1,2)(3,2) = (1,2); (1,3,2);(2);(3,2) и т.д.; –
–  - множество болванов.
- множество болванов. . (5.17)
. (5.17) (5.18а)
(5.18а) . (5.19)
. (5.19) и
и  – любые игры со своей характеристической функцией, то
– любые игры со своей характеристической функцией, то .
.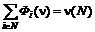 .
. ,
,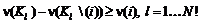 ,
, .
.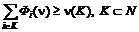 .
. . Заменим в соотношении (5.17)
. Заменим в соотношении (5.17)  , (5.22)
, (5.22)
 .
. (5.23)
(5.23)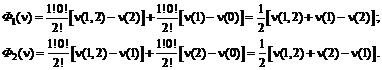 (5.24)
(5.24) (5.25)
(5.25) ,
, , поэтому
, поэтому  .
. .
. (5.26а)
(5.26а)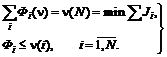 (5.26б)
(5.26б) +
+  – точка принадлежит Парето-множеству;
– точка принадлежит Парето-множеству; 
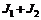 ) являются диагонально противоположными вершинами квадрата. Точка Шепли всегда лежит на линии, проведённой из точки min(
) являются диагонально противоположными вершинами квадрата. Точка Шепли всегда лежит на линии, проведённой из точки min( 
 , (5.31)
, (5.31) ;iÎN}, J* – идеальная точка векторной оптимизации [246].
;iÎN}, J* – идеальная точка векторной оптимизации [246].
 (5.32)
(5.32) (5.33)
(5.33)





 5.5. Применение двухэтапного метода для получения
5.5. Применение двухэтапного метода для получения  ,
,




 , где
, где  (рис. 5.5 и 5.6).
(рис. 5.5 и 5.6). (рис. 5.5, 5.6);
(рис. 5.5, 5.6); (рис. 5.5);
(рис. 5.5); (рис. 5.6).
(рис. 5.6).
 .
.


