
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Обобщение характеристической функции, предпосылка игры, делёж и его свойстваСтр 1 из 2Следующая ⇒ Рассмотрим обобщение понятия характеристической функции на основе Нэш-равновесия. Определение 5.1. Характеристической функцией игры (в типичном случае «без приоритетов» Далее, без ограничения общности будем считать величины Тогда характеристическая функция для коалиции где Характеристическая функция для коалиции В отличие от традиционных структур характеристической функции (5.3) введение характеристической функции более общего вида (5.1) повышает значимость оценки самостоятельных действий коалиции (или игрока), так как по определению
Определение 5.2. Характеристическая функция обладает следующими свойствами: 1) 2)  3) cупераддитивность 4) Следует отметить, что вид характеристической функции, в общем случае игры, может отличаться от данного определением 5.1. В каждой игре характеристическая функция Определение 5.3 [199]. Дележом для кооперативного компромисса 1) 2) Замечание.Для предпосылки дележа игры условие коллективной рациональности имеет вид Понятие дележа существенно отличает кооперативную игру от бескоалиционной. Бескоалиционные игры являются стратегическими в том смысле, что исход игры формируется в результате действий тех игроков, которые в исходе получают те или иные выигрыши. Исходом кооперативной игры является делёж, который возникает не как следствие действий игроков, а как результат их соглашений. То есть в кооперативных играх сравниваются по предпочтительности не действия с исходами, а дележи, и сравнение это не ограничивается рассмотрением индивидуальных выигрышей, а носит более содержательный характер. Условием существования наилучшего дележа является свойство трансферабельности выигрышей коалиции Определение 5.4[42]. Несущественной игрой называется кооперативная игра с аддитивной характеристической функцией, когда Утверждение 5.1 [199]. Всякая кооперативная игра двух игроков с постоянной суммой несущественна. Доказательство. По свойству 5.4 характеристической функции (определение 5.2) Утверждение 5.2. Для того чтобы характеристическая функция Утверждение 5.3. В несущественной игре имеется только один делёж Несущественность игры может быть следствием нетрансферабельности выигрышей и преодолена изменениями в постановке задачи или модификацией метода исследования. Так, в работе [199] показана нетрансферабельность типичного терминального показателя где В работе [199] предложена модификация понятия дележа, которая приводит к формированию характеристических множеств взамен характеристических функций и к решению задачи определения оптимального дележа. Возможным представляется и способ, когда вводится понятие взвешенного вектора потерь коалиции и в зависимости от Методы оптимизации дележей Принципы оптимальности классической теории кооперативных игр, заданных в форме характеристических функций, условно можно разделить на два типа [32]: 1) оптимальность на основе принципов устойчивого поведения каждого игрока (оптимальность по Парето, С-ядро, Н–М-решение); 2) оптимальность на основе «здравых» гипотез о свойствах, которыми должно обладать решение, исходящее от явно или неявно существующего арбитра (вектор Шепли, арбитражные схемы, среднеквадратическое решение). Рассмотрим в сравнении оптимизационные подходы на основе понятий Парето, С-ядра, Н–М-решений и определения вектора дележа Шепли в классе дифференциальных игр [32, 199], но при условии, что целью каждого игрока системы является выбор параметров Из свойства коллективной рациональности дележа следует, что предпосылки дележа оптимальны по Парето, но из свойства индивидуальной рациональности следует, что не все решения по Парето являются предпосылками дележа. Утверждение 5.4. Парето-граница Парето–Нэш-множества компромиссов однотипных ММС содержит множество предпосылок дележей. Доказательство. Как известно, Парето–Нэш-множество составляет прямоугольный многомерный конус с вершиной в Характеристическая функция (5.1) имеет вид Сравнение равновесия Условие коллективной рациональности выполняется тождественно поэтому предпосылки дележей принадлежат Парето-решениям П–Н-мно-жества компромиссов. Данное утверждение очевидно для Утверждение теоремы очевидно и для характеристической функции вида (5.3). В этом случае по определению так как равновесные значения функционалов «не хуже» [32], чем гарантированные. Поэтому Далее, в данном пункте приводятся основные определения и утверждения кооперативных игр в форме характеристической функции касающиеся понятий доминирования дележей, решения в форме С-ядра, Нейман-Моргенштерн-решения и их свойств. Определение 5.5. Дележ Первое условие очевидно, а второе условие означает, что члены коалиции в состоянии реализовать делёж, т.е. сумма выигрышей членов коалиции не должна превосходить уверенно получаемое ею количество, имеющего смысл приближения локального Парето-решения в равновесии Определение 5.6 [199]. Дележ Определение 5.7 [199]. Множество всех недоминируемых дележей в кооперативной игре называется её С-ядром. Любой делёж из С-ядра устойчив, так как ни одна коалиция не имеет желания изменить его. Утверждение 5.5. Если множество значений v является выпуклым, то С-ядро не является пустым множеством. Главное основание утверждения – свойство супераддитивности v, при котором v выпуклая1. Следствие 5.1 [42]. Для несущественной игры С-ядро существует и состоит из единственного дележа. Следствие 5.2 [42]. Во всякой существенной игре с постоянной суммой С-ядро пусто. Утверждение 5.6 [42, 199]. Для того, чтобы дележи Jd принадлежали для любой коалиции K ÌN [K ¹ N, |K| >l), где |K| – мощность множества K. В работе [199] дана интерпретация результата в дифференциальных играх и сформулированы сложные условия оптимальности. В работе [42] дан способ формирования С-ядра в общих играх трёх лиц. Всё же часто С-ядро оказывается пусто. Определение 5.8. Множество дележей L называется Нейман–Моргенштерн (Н–М)-решением с характеристической функцией Утверждение 5.7 [42].Если в кооперативной игре существует С-ядро С- и Н–М-решение L, то C Ì Z. Методы поиска Н–М-решения трёх лиц даны в работе [42]. Некоторые интерпретации для дифференциальных игр на уровне условий и свойств оптимизационного подхода даны в работе [199]. В общем случае [42] неизвестно каких-либо критериев, позволяющих судить о наличии у кооперативной игры Н–М-решения. При наличии Ввиду больших сложностей при определении существования и в способах отыскания оптимальных дележей на основе С-ядра и Н–М-решений в играх общего вида особого внимания заслуживает подход на основе вектора Шепли, который на основе обоснованных предположений даёт практически реализуемое правило формирования оптимального дележа. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 207. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 лиц {
лиц {  } называется вещественная функция
} называется вещественная функция  , определённая на подмножествах множества
, определённая на подмножествах множества  равновесное значение (для
равновесное значение (для  ) бескоалиционной игры (или гарантирующее значение антагонистической игры) двух лиц, которую сыграли бы
) бескоалиционной игры (или гарантирующее значение антагонистической игры) двух лиц, которую сыграли бы  (множество
(множество 
 , где
, где  – число элементов
– число элементов  показателя эффективности
показателя эффективности  выигрышами систем-игроков. Для показателей потерь все неравенства в определениях и результатах меняются на противоположные.
выигрышами систем-игроков. Для показателей потерь все неравенства в определениях и результатах меняются на противоположные. (5.1)
(5.1) находятся из системы неравенств
находятся из системы неравенств (5.2)
(5.2) (5.3)
(5.3)


 (
(  – для минимизируемых
– для минимизируемых  (
(  для минимизируемых
для минимизируемых  (для игр с постоянной суммой
(для игр с постоянной суммой  ).
).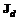 , удовлетворяющий условиям:
, удовлетворяющий условиям: (коллективная рациональность);
(коллективная рациональность); (индивидуальная рациональность) для всех
(индивидуальная рациональность) для всех  (5.4)
(5.4)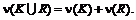 (5.5)
(5.5) , а это означает аддитивность функции при
, а это означает аддитивность функции при  .
. была аддитивной, необходимо и достаточно, чтобы выполнялось равенство
была аддитивной, необходимо и достаточно, чтобы выполнялось равенство . (5.6)
. (5.6) . Во всякой существенной игре множество дележей бесконечно.
. Во всякой существенной игре множество дележей бесконечно.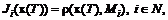 (5.7)
(5.7) - некоторая заданная система точек в пространстве
- некоторая заданная система точек в пространстве  , которому принадлежит вектор состояния
, которому принадлежит вектор состояния  , который в свою очередь оценивает расстояние r от положения игроков в момент окончания игры до точек
, который в свою очередь оценивает расстояние r от положения игроков в момент окончания игры до точек  , являющихся для них известными. Потери
, являющихся для них известными. Потери  не являются трансферабельными, так как не могут делиться и передаваться другим участникам игры. По существу это означает, что каждой точке
не являются трансферабельными, так как не могут делиться и передаваться другим участникам игры. По существу это означает, что каждой точке  (5.8)
(5.8) «делятся» степени близости к
«делятся» степени близости к  ,т.е. в зависимости от
,т.е. в зависимости от  формируется множество дележей внутри коалиции
формируется множество дележей внутри коалиции  своей полной математической модели, в частности, выбор параметров ПКЗУ с оптимизацией своего показателя – функционала общего вида.
своей полной математической модели, в частности, выбор параметров ПКЗУ с оптимизацией своего показателя – функционала общего вида.
 , ограниченный Парето-границей
, ограниченный Парето-границей 
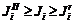 .
. , при этом
, при этом (5.9)
(5.9) и
и  показывает, что для однотипных систем с равными ресурсами оптимизация суммы имеет эффект локальной Парето-оптимизации. Поэтому ситуация равновесия
показывает, что для однотипных систем с равными ресурсами оптимизация суммы имеет эффект локальной Парето-оптимизации. Поэтому ситуация равновесия  и уменьшения эффективности для системы
и уменьшения эффективности для системы  . Следовательно, выполняется условие индивидуальной рациональности дележа
. Следовательно, выполняется условие индивидуальной рациональности дележа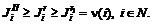 (5.10)
(5.10) , (5.11)
, (5.11) .
.
 , таким образом, Парето-граница П–Н-мно-жества содержит предпосылки дележей, среди которых может быть выбран наилучший.
, таким образом, Парето-граница П–Н-мно-жества содержит предпосылки дележей, среди которых может быть выбран наилучший. доминирует дележ
доминирует дележ  по коалиции
по коалиции  , если:
, если: для всех
для всех  ,
, . (5.12)
. (5.12) . Иначе, встретившись с дележом, дающим столько, сколько коалиция самостоятельно не в состоянии добиться, должна согласиться на него и не заниматься его сравнением с другими дележами.
. Иначе, встретившись с дележом, дающим столько, сколько коалиция самостоятельно не в состоянии добиться, должна согласиться на него и не заниматься его сравнением с другими дележами. . Доминирование по коалиции, состоящее из одного игрока, а также по множеству всех игроков невозможно, так как в этом случае нарушаются первое и второе свойство дележа.
. Доминирование по коалиции, состоящее из одного игрока, а также по множеству всех игроков невозможно, так как в этом случае нарушаются первое и второе свойство дележа. (5.13)
(5.13)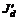 ,
,  Î L следует, что
Î L следует, что  ещё не определяет выигрыша каждого из игроков.
ещё не определяет выигрыша каждого из игроков.