
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники равны.
Человек, рост которого 1.6 м, стоит на расстоянии 3 м от уличного фонаря. При этом длина его тени равна 2 м. Определите высоту фонаря (в м).
8. В параллелограмме ABCD точка M — середина стороны AB. Известно, что MC = MD. Докажите, что данный параллелограмм — прямоугольник. Вариант 8. Периметр равностороннего треугольника ABC равен 36 см. Найдите длину средней линии этого треугольника.
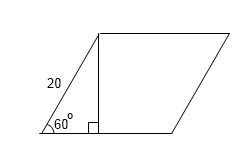
2.Сторона ромба равна 20, а острый угол равен 60°. Найдите Длину меньшей диагонали ромба.
3.Из прямоугольника со сторонами 6 см и 8 см вырезан квадрат со стороной 4 см. Найдите площадь оставшейся части. Ответ дайте в см².
4.Точка О — центр окружности, угол BAC = 70° (см. рисунок). Найдите величину угла BOC (в градусах).
5. Укажите в ответе номера неверных утверждений. 1) Два угла с общей стороной называются смежными. 2) На прямой можно отложить только один отрезок заданной длины. 3) Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Человек, рост которого 2 м, стоит на расстоянии 3,5 м от уличного фонаря. При этом длина его тени равна 1 м. Определите высоту фонаря (в м).
Найдите величину угла AOE, если OE – биссектриса угла AOC, OD — биссектриса угла COB. 8. В параллелограмме ABCD точка K – середина стороны AB. Известно, что KC = KD. Докажите, что данный параллелограмм — прямоугольник.
Средняя линия равностороннего треугольника ABC равна 8 см. Найдите периметр этого треугольника.
2. Сторона ромба равна 36, а тупой угол равен 120°. Найдите длину меньшей диагонали ромба. 
4. Точка O — центр окружности, угол BAC = 75° (см. рисунок). Найдите величину угла BOC (в градусах). 5. Укажите в ответе номера верных утверждений: 1) Существует параллелограмм, диагонали которого равны. 2) Через точку, лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой. 3) Если две стороны одного треугольника соответственно равны двух сторонам другого треугольника, то такие треугольники равны. Столб высотой 9 м отбрасывает тень длиной 2 м. Найдите длину (в м) тени человека ростом 1,8 м, стоящего около этого столба.
Найдите величину угла COE, если OE — биссектриса угла AOC, OD – биссектриса угла COB. Противоположные углы четырехугольника попарно равны. Докажите, что этот четырехугольник — параллелограмм. Вариант 10.
Средняя линия равностороннего треугольника ABC равна 7 см. Найдите периметр этого треугольника.
2. Сторона ромба равна 20, а острый угол равен 60° . Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
3. Из квадрата со стороной 8 см вырезан прямоугольник со сторонами 3 см и 2 см. Найдите площадь оставшейся части. Ответ дайте в см².
5. Укажите в ответе номера верных утверждений: 1) Если у параллелограмма есть один прямой угол, то этот параллелограмм — прямоугольник. 2) Через две точки плоскости можно провести две различные прямые. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 1411. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

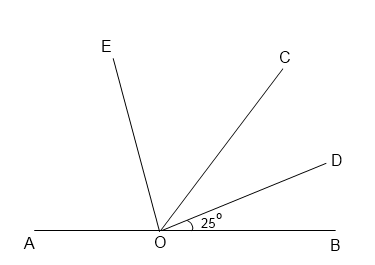
 7. Найдите величину угла DOB, если OE — биссектриса угла AOC, OD — биссектриса угла COB.
7. Найдите величину угла DOB, если OE — биссектриса угла AOC, OD — биссектриса угла COB.





 3. Из квадрата со стороной 10 см вырезан прямоугольник со сторонами 3 см и 4 см. Найдите площадь оставшейся части. Ответ дайте в см².
3. Из квадрата со стороной 10 см вырезан прямоугольник со сторонами 3 см и 4 см. Найдите площадь оставшейся части. Ответ дайте в см².

 4. К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.
4. К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.