
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Определяем напряжения, токи и полные комплексные мощности фаз для нагрузки, соединенной в «звезду»8. Выполняем преобразование трехфазной электрической цепи (см. рис. 4.1) для соединения нагрузки «звездой», учитывая, что в соответствующие фазы нагрузки включены элементы, представленные на рис. 4.2. Полученный после преобразования участок трехфазной цепи показан на рис. 4.3. На этом же рисунке показаны условные направления токов и напряжений. 9. Пренебрегая сопротивлением линейных проводов, условимся, что к фазам нагрузки приложены напряжения, равные фазным напряжениям источника. Тогда в соответствии с (3.14) можем записать:
10. На основании закона Ома в соответствии с выражениями (3.16)-(3.18) определяем комплексы действующих значений фазных токов:
Запишем действующие значения фазных токов:
11. На основании первого закона Кирхгофа для узла nв соответствии с выражением (3.30) определяем ток в нейтральном проводе:
Определяем действующее значение тока в нейтральном проводе
12. Совмещенная векторная диаграмма фазных токов и напряжений на комплексной плоскости показана на рис. 4.4. Масштабы: по току
Рис. 4.4 Для нагрузки, фазы которой соединены в «звезду», существует еще один способ решения, основанный на использовании действующих значений напряжений и токов. Рассмотрим методику решения данным способом. Определяем действующие значения фазных напряжений нагрузки на основании (4.1) с учетом (3.14)
 Определяем величины полных сопротивлений фаз в соответствии с (4.13):
На основании закона Ома в соответствии с выражениями (3.16)-(3.18) определяем действующие значения фазных токов
При построении векторной диаграммы условимся, что вектор фазного напряжения Чтобы отложить векторы фазных токов, определим угол сдвига между током и напряжением для каждой фазы нагрузки по формуле (1.26):
В соответствии с выражением (3.30) вектор тока в нейтральном проводе |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 196. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ; (4.24)
; (4.24) ;(4.25)
;(4.25) . (4.26)
. (4.26)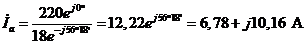 ; (4.27)
; (4.27)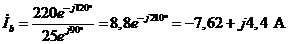 ; (4.28)
; (4.28) . (4.29)
. (4.29) ; (4.30)
; (4.30) ; (4.31)
; (4.31) . (4.32)
. (4.32)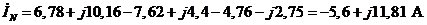 .(4.33)
.(4.33) . (4.34)
. (4.34) ; по напряжению
; по напряжению  .
.
 . (4.35)
. (4.35) ; (4.36)
; (4.36) ; (4.37)
; (4.37) . (4.38)
. (4.38)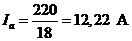 ; (4.39)
; (4.39) ; (4.40)
; (4.40) . (4.41)
. (4.41) нагрузки совпадает с действительной осью комплексной плоскости. Строим вектор фазного напряжения
нагрузки совпадает с действительной осью комплексной плоскости. Строим вектор фазного напряжения  , отстающим от вектора
, отстающим от вектора  - опережающим вектор
- опережающим вектор  ; (4.42)
; (4.42)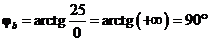 ; (4.43)
; (4.43) . (4.44)
. (4.44) может быть определен как геометрическая сумма векторов фазных токов. Данный прием показан на векторной диаграмме (см. рис. 4.4). Чтобы определить действующее значение тока
может быть определен как геометрическая сумма векторов фазных токов. Данный прием показан на векторной диаграмме (см. рис. 4.4). Чтобы определить действующее значение тока  с помощью векторной диаграммы, необходимо умножить длину вектора на масштаб тока.
с помощью векторной диаграммы, необходимо умножить длину вектора на масштаб тока.