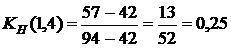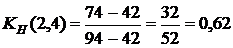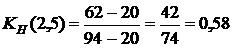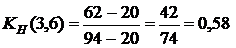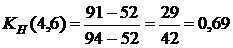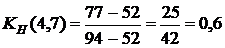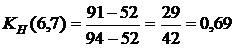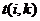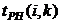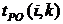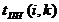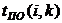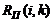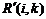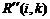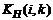Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Коэффициенты эластичности результативного показателя по факторам определяются по формуле (24) ⇐ ПредыдущаяСтр 2 из 2
Коэффициент эластичности В соответствии с моделью (20)
где Итак, если общие затраты Предположим, что мы хотим распространить построенную модель на другие значения факторных переменных и решить проблему прогнозирования среднего значения
Вычислим прогноз для семьи с общими затратами
5 РАНГОВАЯ КОРРЕЛЯЦИЯ Анализ экономических процессов сталкивается с необходимостью изучения показателей, которые не имеют количественного измерителя. Это социологические, обобщенные социально-экономические характеристики, которые влияют на ход экономического процесса. Например, решение вопроса удовлетворения спроса на товары зависит от ассортимента товаров, уровня взаимоотношений производителей с потребителями, условий транспортировки и хранения продукции и других факторов, которые собственного измерителя не имеют. В этом случае вводят систему рангов и для анализа используют методы ранговой корреляции.  Алгоритм исследования имеет три этапа. Вначале определяют систему рангов, порядок их присвоения, формируют группу экспертов, которые распределяют ранги. Находя сумму рангов для факторов, их упорядочивают. На следующем этапе проверяют меру согласованности мнений экспертов с помощью коэффициентов ранговой корреляции. На последнем этапе устанавливается значимость именно коэффициентов ранговой корреляции. Случай двух экспертов Пример 6. Работники двух фирм оценили влияние 10 обобщенных факторов на хозяйственную деятельность фирм. Наибольшее значение ранга присваивалось самому существенному показателю. Необходимо провести статистический анализ результатов опроса.
где Решение. 1) Определим сумму рангов каждого фактора, а также среднее значение ранга
Расчеты свидетельствуют, что наиболее значимыми, по мнению опрашиваемых, следует назвать 3, 6, 7 и 9 факторы, а наименее существенными – 8, 4, 5 и 2 факторы. 2) Проверим согласованность мнений экспертов по критерию Спирмена. а) Найдем коэффициент ранговой корреляции Спирмена по формуле (26):
В нашем случае
Полученное значение свидетельствует о высокой степени согласованности мнений экспертов относительно влияния факторов ( б) Установим, будет ли значимым коэффициент Спирмена: Критическую точку
где В нашем случае Поскольку 3) Проверим согласованность экспертов по критерию Кендалла. а) Найдем коэффициент ранговой корреляции Кендалла: для этого ранги первого эксперта разместим в возрастающий последовательности, ранги второго перенесем соответственно. Таблица 11 – Вспомогательные расчеты
Для каждого элемента второго ряда подсчитываем число рангов, которые его превосходят и расположены за ним. Подытоживая эти числа, получаем величину
Коэффициент ранговой корреляции Кендалла находим по формуле (28):
В нашем случае формула (28) имеет вид Рассчитанный коэффициент подтверждает вывод, сделанный раньше: между экспертами существует высокая согласованность мнений о влиянии факторов. б) Значимость коэффициента Кендалла проверяем, используя критическую точку, которую находят по формуле (29):
где В нашем случае Поскольку Случай многих экспертов Пример 7. Представители 10 предприятий провели ранжирование 10 показателей, которые влияют на коммерческую работу. Наибольшее значение присваивалось наиболее значительному показателю. Необходимо провести эконометрический анализ результатов ранжирования.
Решение. Вычисление суммы рангов для всех показателей позволяет сделать следующий вывод: по мнению всех экспертов, самое значительное влияние на коммерческую деятельность осуществляют 3, 7 , 6 и 1 факторы, наименьшее влияние –5, 8, 2 и 4 факторы. Меру согласованности мнений экспертов проверим с помощью коэффициента конкордации, который находят по формуле (30):
где В нашем примере
Надо подчеркнуть, что согласованность мнений десяти экспертов достаточно высокая. Оценка значимости коэффициента конкордации проводится следующим образом: - рассчитывают - по таблице (приложение 3) находят критическое значение - сравнивают фактическое и критическое значения. Для рассмотренного примера имеем: Мы видим, что Замечание 1. Необходимо помнить, что Замечание 2. Если одни и те же факторы анализируют два эксперта, а потом большее количество экспертов, то целесообразно составить сравнительную таблицу. В частности, для рассмотренного примера имеем: Таблица 12 – Сравнительные значения
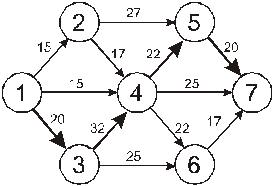
Перечень несущественных факторов не изменился, их порядок стал другим. Относительно существенных факторов, то в них, кроме порядка, изменился и перечень. Ясно, что предпочтение надо отдать случаю с десятью экспертами. Замечание 3. Из таблицы рангов можно отобрать наиболее компетентных экспертов – это те, чьи ранги более всего совпадают со средними значениями. В рассмотренном примере такими являются первый, третий и восьмой эксперты. СЕТЕВОЕ ПЛАНИРОВАНИЕ Основой решения задач, которые связаны с проектированием и выполнением комплекса работ, является системное рассмотрение работ и событий в их взаимосвязи и разработка рекомендаций по усовершенствованию их выполнения. Идея метода сетевого управления и планирования базируется на безмасштабном графическом изображении комплекса операций, которое показывает технологическую последовательность и логическую взаимосвязь между всеми работами комплекса. Основными элементами сетевого графика являются а) работа – любые действия, трудовые процессы, которые сопровождаются затратами времени и приводят к определенным результатам; б) событие – результат окончания одной или несколько работ. Работы в сетевом графике изображают стрелками произвольной длины, а события – кружками, в которых указывают номер события. Пример 8. Построить в соответствии с правилами сетевой график и рассчитать его основные параметры:
Решение.Правила построения сетевого графика: 1) стрелки-работы не должны пересекаться; 2) график должен иметь линейную структуру, то есть события с меньшим номером располагают левее событий, которые имеют больший номер; 3) начальное событие не имеет входных стрелок; 4) конечное событие не имеет исходных стрелок; 5) два события связывает только одна работа; 6) в сети не должно быть событий, в которые не входит ни одна работа, и событий, из которых не выходит ни одна работа. Строим в соответствии с правилами сетевой график, который изображен на рисунке 1.
Рисунок 1 – Сетевой график 1. Выпишем все полные пути и найдем их продолжительности – это пути от начального события к конечному:
Самый продолжительный путь является критическим. В данном случае критическим является путь 2.а. Вычислим ранние сроки событий
Ранний срок указывает наиболее ранний момент времени, к которому завершатся все работы, которые происходили к этому событию. Начальное событие 1 имеет нулевой ранний срок
Последнее число является критическим сроком всего комплекса работ 2.б. Вычислим поздние сроки событий
Поздний срок указывает наиболее поздний момент времени, после которого остается ровно столько времени, сколько необходимо для завершения всех работ, которые следуют за этим событием. Для конечного события поздний срок равняется критическому сроку
Для начального события 1 ранний и поздний сроки совпадают. 2.в. Вычислим резервы времени события Он характеризует предельный срок, на который можно задержать свершения события без изменения критического срока.
События, которые принадлежат критическому пути, не имеют резервов времени. События 2 и 6 можно задержать на 20 и 3 (недель, месяцев) соответственно без изменения критического срока. Удобно занести все найденные характеристики событий в таблицу 13: Таблица 13 - Характеристики событий
3. На основе таблицы составим другую для работ, используя следующие характеристики: - раннее начало работы
В нашем случае по формуле (34) имеем:
- раннее окончание работы В нашем случае по формуле (35) имеем:
- позднее начало работы
В нашем случае по формуле (36) имеем:
- позднее окончание работы
В нашем случае по формуле (37) имеем:
- полный резерв времени работы Он определяет максимальное количество времени, на которое возможно задержать начало работы или увеличить ее продолжительность без изменения критического срока. В нашем случае по формуле (38) имеем:
- резерв времени І рода В нашем случае по формуле (39) имеем:
- резерв времени ІІ рода
В нашем случае по формуле (39) имеем:
- коэффициент напряженности работы
где Он определяет степень срочности работы, позволяет установить очередь их выполнения, если она не определена технологическими связями робот. В нашем случае для определения коэффициента напряженности (40) работы (1,2) находим путь наибольшей продолжительности, который проходит через эту работу – это путь
Таблица 14 - Характеристики работ
ВЫВОДЫ: 1. Критический срок выполнения комплекса работ составляет 94 временные единицы, то есть все работы данного комплекса можно выполнить за наименьший срок в 94 временные единицы (дни, недели, месяцы и т.п.). 2. События 1, 3, 4, 5, 7 являются критическими, они принадлежат критическому пути сетевого графика. Эти события не имеют резерва времени, то есть их нельзя отложить. 3. События 2 и 6 имеют резервы времени 20 и 3 временные единицы соответственно. 4. Работы (1,3), (3,4), (4,5), (5,7) являются критическими и имеют коэффициент напряженности 1. Их выполнение нельзя отложить и невозможно увеличить срок выполнения этих работ. 5. Комплекс не имеет подкритических работ. 6. Работы (2,4), (2,5), (3,6), (4,6), (4,7), (6,7) являются промежуточными. Их должны выполнять в первую очередь после работ критического пути. Наиболее напряженными после работ критического пути являются работы (4,6) и (6,7). 7. Работа (1,4) является ненапряженной, она имеет определенный резерв для увеличения ее продолжительности или задержки начала выполнения.
К О Н Т Р О Л Ь НА Я Р А Б О Т А Внимание! 1. Вариант следует выбирать по двум последним цифрам зачетной книжки. 2. Работу выполнять в отдельной тетради.
Задача 1.
1. Представить динамический ряд графически.
2. Построить модель динамики исследуемого показателя, применив для аппроксимации линейную, параболическую и гиперболическую зависимости.
3. Выполнить оценку построенных моделей на адекватность и надежность, а также выбрать наиболее предпочтительную.
4. Изобразить графически модель, которая признана наилучшей.
5. Составить прогноз показателя на два года. Х – годы, Y – экономический показатель.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 282. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
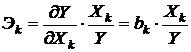 (24)
(24)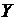 по
по 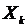 определяет влияние этого фактора на показатель. Если
определяет влияние этого фактора на показатель. Если 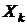 изменится на 1%, то
изменится на 1%, то 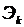 %. Поскольку для линейной регрессии коэффициент эластичности зависит от
%. Поскольку для линейной регрессии коэффициент эластичности зависит от 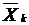 и
и 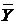 .
.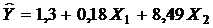 коэффициенты эластичности, найденные по формуле (24) для факторных переменных, равняются:
коэффициенты эластичности, найденные по формуле (24) для факторных переменных, равняются: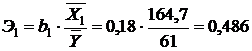 ;
;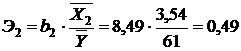 ,
,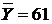 ,
, 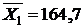 ,
, 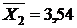 рассчитаны раньше (формулы (17)-(19)).
рассчитаны раньше (формулы (17)-(19)).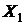 изменятся на 1%, то затраты на питание
изменятся на 1%, то затраты на питание 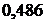 % при условии, что остальные факторы не изменяются. Если количество членов семьи
% при условии, что остальные факторы не изменяются. Если количество членов семьи 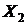 изменится на 1%, то затраты на питание
изменится на 1%, то затраты на питание 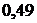 % при условии, что остальные факторы не изменяются.
% при условии, что остальные факторы не изменяются. 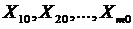 переменных
переменных 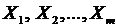 . Эти новые значения
. Эти новые значения 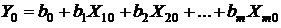 . (25)
. (25)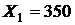 условных денежных единиц и составом семьи
условных денежных единиц и составом семьи 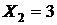 человек. Тогда по формуле (25) следует ожидать, что затраты на питание составят
человек. Тогда по формуле (25) следует ожидать, что затраты на питание составят 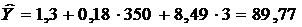 условных денежных единиц.
условных денежных единиц.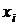
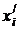
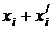
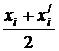
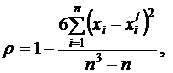 (26)
(26)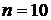 , поэтому формула (26) имеет вид
, поэтому формула (26) имеет вид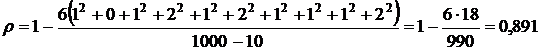
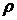 близко к 1).
близко к 1).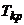 находим по формуле (27):
находим по формуле (27):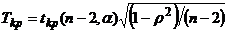 , (27)
, (27)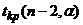 находим по таблице Стьюдента (приложение 5).
находим по таблице Стьюдента (приложение 5).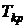 , найденное по формуле (27) равно
, найденное по формуле (27) равно 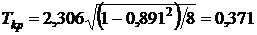 при
при 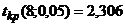 .
.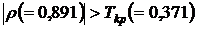 , то ранговую связь факторов следует признать значимой, коэффициенту ранговой корреляции и выводам о существенности факторов надо доверять.
, то ранговую связь факторов следует признать значимой, коэффициенту ранговой корреляции и выводам о существенности факторов надо доверять. . В нашем случае она равняется
. В нашем случае она равняется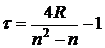 (28)
(28)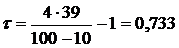 .
.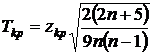 (29)
(29)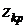 – критическое значение, которое найдем по таблице функции Лапласа из равенства:
– критическое значение, которое найдем по таблице функции Лапласа из равенства: 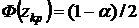 .
.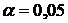 , тогда
, тогда 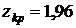 , поэтому
, поэтому 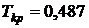 .
.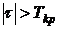 , то ранговая связь между факторами является существенной, коэффициент Кендалла заслуживает доверия, а выводы о влиянии факторов справедливы.
, то ранговая связь между факторами является существенной, коэффициент Кендалла заслуживает доверия, а выводы о влиянии факторов справедливы.
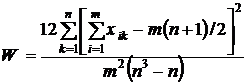 , (30)
, (30)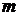 – количество экспертов,
– количество экспертов, 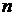 – количество факторов,
– количество факторов, 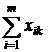 – сумма рангов по каждому фактору.
– сумма рангов по каждому фактору.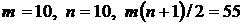 .
.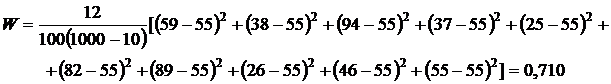
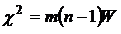 ;
;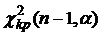 ;
;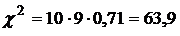 . По
. По 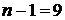 находим в таблице (приложение 3)
находим в таблице (приложение 3) 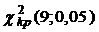 =16,92.
=16,92.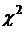 значительно превышает критическую величину, из чего следует, что коэффициенту конкордации нужно доверять и что имеет место достаточно высокая корреляционная зависимость рассматриваемых факторов.
значительно превышает критическую величину, из чего следует, что коэффициенту конкордации нужно доверять и что имеет место достаточно высокая корреляционная зависимость рассматриваемых факторов.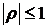 ,
, 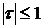 ,
, 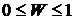 . Чем ближе эти коэффициенты к 1, тем сильнее согласованность мнений экспертов. Чем ближе они к нулю, тем она более слабая.
. Чем ближе эти коэффициенты к 1, тем сильнее согласованность мнений экспертов. Чем ближе они к нулю, тем она более слабая.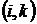
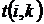
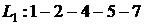
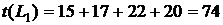
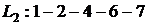
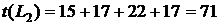
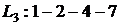
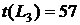
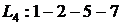
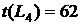
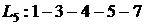
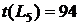
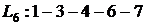
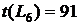
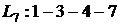
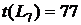
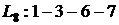
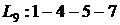
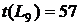
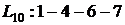
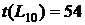
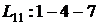
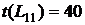
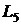 . Он указан на сетевом графике (рисунок 1).
. Он указан на сетевом графике (рисунок 1).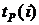 для всех работ
для всех работ 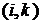 , которые входят в событие
, которые входят в событие 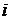 , по формуле (31):
, по формуле (31):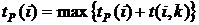 (31)
(31)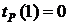 . Для события 2, в которое входит одна работа
. Для события 2, в которое входит одна работа 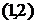 , имеем
, имеем 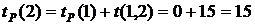 . В событие 3 входит одна работа
. В событие 3 входит одна работа 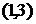 , тогда
, тогда 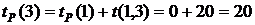 . В событие 4 входят три работы
. В событие 4 входят три работы 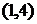 ,
, 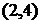 и
и 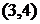 , поэтому
, поэтому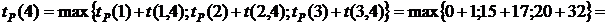
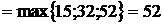 .
.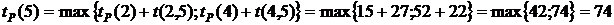 .
.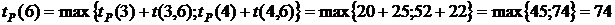 .
.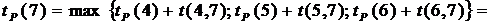
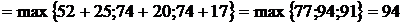 .
.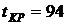 . Он определяет минимальный срок выполнения всего комплекса работ.
. Он определяет минимальный срок выполнения всего комплекса работ.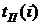 для всех работ
для всех работ 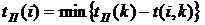 (32)
(32)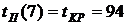 . Из события 6 выходит одна работа, поэтому
. Из события 6 выходит одна работа, поэтому 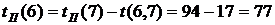 . Из события 5 тоже выходит одна работа, тогда
. Из события 5 тоже выходит одна работа, тогда 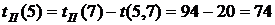 . Из события 4 выходят три работы:
. Из события 4 выходят три работы: 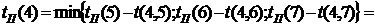
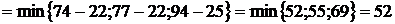 .
.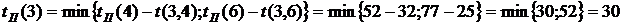 .
.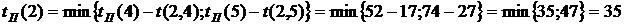 .
.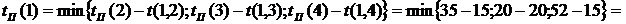
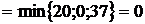 .
.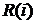 по формуле (33)
по формуле (33)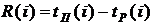 . (33)
. (33)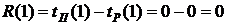
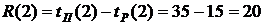
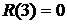
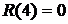
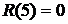
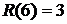
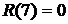
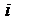
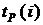
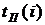
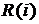
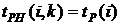 (34)
(34)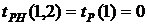
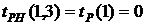
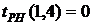
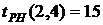
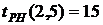
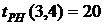
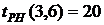
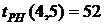
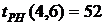
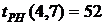
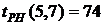
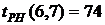
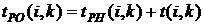 (35)
(35)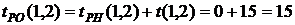
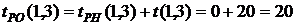
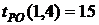
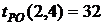
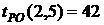
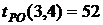
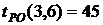
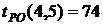
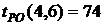
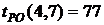
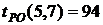
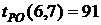
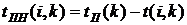 (36)
(36)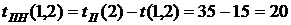
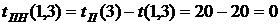
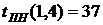
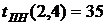
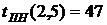
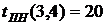
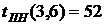
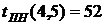
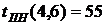
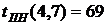
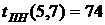
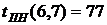
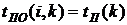 (37)
(37)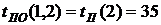
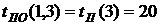
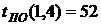
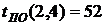
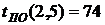
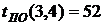
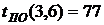
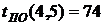
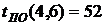
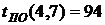
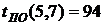
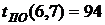
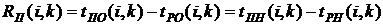 (38)
(38)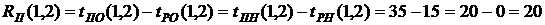
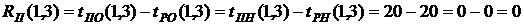
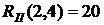
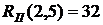
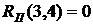
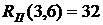
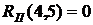
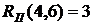
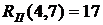
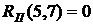
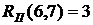
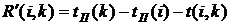 (39)
(39)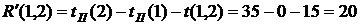
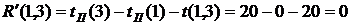
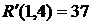
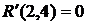
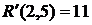
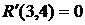
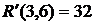
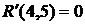
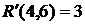
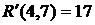
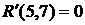
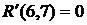
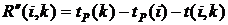 (40)
(40)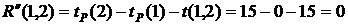
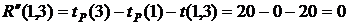
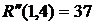
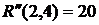
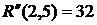
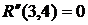
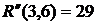
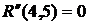
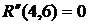
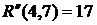
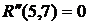
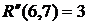
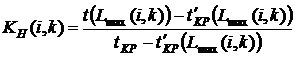 , (40)
, (40)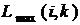 – путь максимальной продолжительности, который проходит через работу
– путь максимальной продолжительности, который проходит через работу  – продолжительность отрезка критического пути, который совпадает с путем
– продолжительность отрезка критического пути, который совпадает с путем 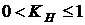 . Работы критического пути имеют коэффициент напряженности 1. Если
. Работы критического пути имеют коэффициент напряженности 1. Если 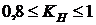 , то работу считают подкритической, сроки ее выполнения жесткие, ее следует выполнять в первую очередь после критических работ. Если
, то работу считают подкритической, сроки ее выполнения жесткие, ее следует выполнять в первую очередь после критических работ. Если 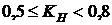 , то работа является промежуточной по степени напряженности срока ее выполнения. Если
, то работа является промежуточной по степени напряженности срока ее выполнения. Если 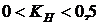 , то работа является ненапряженной, ее выполнение можно отложить на некоторый срок, который определяют резервом времени.
, то работа является ненапряженной, ее выполнение можно отложить на некоторый срок, который определяют резервом времени.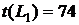 . Проследим на графике, как пройдет этот путь и где он имеет с критическим путем общие участки. Общие участки (4,5) и (5,7) имеют продолжительность 22+20=42, тогда коэффициент напряженности равняется
. Проследим на графике, как пройдет этот путь и где он имеет с критическим путем общие участки. Общие участки (4,5) и (5,7) имеют продолжительность 22+20=42, тогда коэффициент напряженности равняется 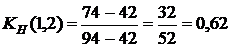 . То есть работа (1,2) является промежуточной по степени напряженности срока ее выполнения. Аналогично рассчитываем другие коэффициенты напряженности, помня, что коэффициент напряженности работ критического пути равняется 1.
. То есть работа (1,2) является промежуточной по степени напряженности срока ее выполнения. Аналогично рассчитываем другие коэффициенты напряженности, помня, что коэффициент напряженности работ критического пути равняется 1.