
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
АВТОКОРРЕЛЯЦИЯ ДАННЫХ И ОСТАТКОВСтр 1 из 2Следующая ⇒ ДОНЕЦКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ЭКОНОМИКИ И ТОРГОВЛИ им. М. ТУГАН-БАРАНОВСКОГО КАФЕДРА ВЫСШЕЙ И ПРИКЛАДНОЙ МАТЕМАТИКИ
Э К О Н О М Е Т Р И Я Учебное пособие
Утверждено на заседании кафедры высшей и прикладной математики. Протокол № от 2002 г.
Одобрено учебно-методическим советом университета. протокол № от 2002 г. ДОНЕЦК 2002 УДК 330. 115
Эконометрия. Учебное пособие. /Cост. Пенина Г.Г., Шепеленко О.В., Узбек Е.К., Орлова Л.М. - Донецк: ДонГУЭТ, 2002. - 79 с.
Учебное пособие предназначено для студентов дневного и заочного отделений экономических специальностей. Его цель – помочь студентам усвоить темы курса эконометрии. Учебное пособие содержит теоретические вопросы, а также решения типовых задач. Даны рекомендации к решению задач, которые предназначены в помощь студентам при выполнении контрольной работы.
Рецензент: Винда Е.В., канд. техн. наук, доцент
© Донецкий государственный университет экономики и торговли им. М.Туган-Барановского, 2002 ВСТУПЛЕНИЕ Эконометрия – это наука, изучающая количественные закономерности и взаимозависимости экономических процессов и объектов с помощью математико-статистических методов и моделей. Возрастающей интерес к эконометрии вызван современным этапом развития экономики в государстве, формированием рыночных отношений. Эконометрия имеет инструментарий, который позволяет перейти от качественного уровня анализа к уровню, который использует количественные статистические значения исследуемых величин. Она рассматривает не отдельные частичные характеристики, а строится на комплексном исследовании всего экономического процесса.  Эконометрия является синтезной дисциплиной; она объединяет в себе экономическую теорию, математическую экономику, экономическую и математическую статистику. Курс эконометрии тесно связан с микроэкономикой, макроэкономикой, финансовым анализом, обеспечивая прикладные знания специалистов. В нем содержатся исследовательские приемы изучения взаимосвязи экономических явлений, выдвигаются и проверяются гипотезы о наличии корреляционных связей между признаками, количественно оценивается существенность взаимосвязей, определяются формы связи и проводится выбор уравнений, оценивается достоверность параметров, строятся однофакторные и многофакторные регрессионные модели, дается оценка их адекватности и надежности. Особое место занимает исследование связи в динамических процессах путем построения авторегрессионных моделей и оценки возможности использования их в прогнозировании. Без эконометрических методов нельзя построить надежного прогноза, а значит – под вопросом и успех в управлении экономическими процессами в бизнесе, банковском деле, финансах. МОДЕЛИ РЯДОВ ДИНАМИКИ
Одной из важнейших задач исследования экономических процессов является изучение изменения экономических показателей с течением времени (товарооборота, объема выпуска продукции, производительности труда и т.д.). Эта задача решается с помощью упорядочения и анализа рядов динамики. Динамическим рядом называется последовательность результатов наблюдений за явлением через равные промежутки времени. Изучая ряды динамики, стремятся обнаружить основную, главную тенденцию в изменении показателей ряда. Аналитическое моделирование рядов динамики проводится с помощью простейших экономико-математических моделей: линейной, параболической, гиперболической, логарифмической, показательной, степенной и других. Пример 1. Проанализировать показатели реализации мучных изделий в государственной торговле Донецкой области за ряд лет. Найти уравнения линейной, параболической и гиперболической зависимостей. Проверить адекватность полученных экономико-математических моделей, определить наилучшую модель.
Решение.Данные таблицы показывают, что реализация продукции неуклонно возрастала, хотя происходило это неравномерно. Очевидно, существует ряд факторов, под влиянием которых изменяется величина объема реализации. Некоторые из факторов могут действовать долгосрочно, а другие – кратковременно; некоторые могут быть важными, другие – случайными. Для выравнивания показателя реализации мучных изделий в государственной торговле будем использовать такие функции: линейную, параболическую и гиперболическую. Параметры избранных для моделирования функций можно найти с помощью метода наименьших квадратов. На его основе для каждой из функций формируют специальную систему уравнений Гаусса. Для указанных функций приведем соответствующие системы:
В любой из систем (1)-(3) Отсчет временного показателя
Таблица 1 - Вспомогательные расчеты для формирования систем Гаусса
В последней строке таблицы 1 указаны суммы всех значений для каждого столбца. Составим системы для трех функций и найдем соответствующие уравнения. Для определения параметров уравнения линейной функции запишем систему уравнений (1) и найдем ее решение:
Таким образом, Для определения параметров уравнения параболической функции
Таким образом, Для определения параметров уравнения гиперболической функции запишем систему уравнений (3) и найдем ее решение
Таким образом,
Адекватность экономико-математической модели может быть установлена с помощью средней ошибки аппроксимации (среднего процента расхождения теоретических и фактических значений):
где
Для этого по каждому уравнению находят теоретические значения
При моделировании экономических показателей чаще всего допускается 5% погрешность (иногда 7%, редко 10%). Модель считается адекватной (то есть пригодной), если
Выбор наилучшей модели можно проводить на основе остаточного среднеквадратичного отклонения (остаточной дисперсии):
где Лучшей будет та функция, для которой значение
Таблица 2 - Расчеты для линейной функции
Из формул (4), (5) имеем:
Таблица 3 - Расчеты для параболической функции
Из формул (4), (5) имеем: Таблица 4 - Расчеты для гиперболической функции
Из формул (4), (5) имеем: то эта модель адекватной не является и считать для нее Составим сводную таблицу для статистических оцениваемых характеристик: Таблица 5 - Статистические оценки для исследуемых моделей
Из сравнения средних ошибок аппроксимации видно, что для гиперболической функции она выходит за 5% уровень, у линейной модели и параболической эта характеристика не выходит за 5% уровень и приблизительно одинаковая. Если оценивать преимущество, то очевидно, что лучшей есть параболическая функция, поскольку у нее остаточное среднеквадратичное отклонение АВТОКОРРЕЛЯЦИЯ ДАННЫХ И ОСТАТКОВ В процессе исследования экономических явлений в качестве исходных статистических значений используют экономические величины, характеризующие размер исследуемых показателей и требующие эконометрического анализа и оценки. При этом следует иметь в виду, что показатели временных рядов часто имеют нежелательные особенности: следующее значение в определенной мере зависит от предшествующих значений. Такое явление получило название автокорреляции. Автокорреляция данных Автокорреляцией данныхназывается явление взаимосвязи следующих значений показателя от его предшествующих значений. Наличие автокорреляции данных ведет к ухудшению уравнения регрессии, увеличению величины ошибок оценок параметров, расширению доверительных интервалов, снижению показателей значимости. Выявление автокорреляции, возможное ее исключение или уменьшение до допустимого уровня делает дальнейшее моделирование зависимости экономических признаков и прогнозирование более надежным и достоверным. Для уменьшения автокорреляции абсолютных значений показателей существуют разные способы. Почти все они основаны на исключении главной временной тенденции (тренда) из начальных данных. Пример 2. Провести проверку на автокорреляцию данных динамического ряда, который исследуется в примере 1. Решение. Уровень автокорреляции измеряют с помощью нециклического коэффициента автокорреляции первого порядка, который равняется парному коэффициенту корреляции между исходным временным рядом и рядом, смещенным на один период:
Построим вспомогательную таблицу для расчета нециклического коэффициента автокорреляции первого порядка: Таблица 6 – Расчет коэффициента автокорреляции
По формуле (6) имеем: Для того, чтобы сделать вывод о наличии автокорреляции в исследуемом динамическом ряду фактическое значение коэффициента сравнивают с критическим В нашем случае критическое значение коэффициента равняется Автокорреляция остатков Методика применения метода наименьших квадратов предполагает, что значения случайной переменной попарно не коррелированы, или они попарно независимы в вероятностном смысле. Если же переменные содержат тренд или циклические колебания, то последовательные остатки могут быть коррелированы. Такой вид корреляции называется автокорреляцией остатковиливозмущений. Автокорреляция остатков затрудняет применение классических методов анализа временных рядов. В моделях регрессии, которые описывают зависимости между случайными значениями взаимозависимых величин, она снижает эффективность применения МНК. Для определения автокорреляции остатков используют критерий Дарбина-Уотсона. Пример 3. Провести проверку параболической функции, построенной в примере 1, на наличие автокорреляции остатков. Решение. Параболическая функция, которая построена в примере 1, имеет вид: Для проверки ее на наличие автокорреляции с помощью критерия Дарбина-Уотсона рассчитывается d-статистикапо формуле (7):
где Для того, чтобы рассчитать d-статистику построим вспомогательную таблицу: Таблица 6 - Расчет d-статистики
С помощью формулы (7) рассчитываем d – статистику:
Вычисленное значение d сравнивается с интервалами, найденными в соответствии со значениями Таблица 7 – Расчет интервалов
Из таблицы 7 видим, что d - статистика удовлетворяет неравенству: 1,32 < 2,136 < 2,68, значит принимаем гипотезу об отсутствии автокорреляции остатков. Замечание.Если значение d-статистики удовлетворяет неравенствам МУЛЬТИКОЛЛИНЕАРНОСТЬ
На практике при количественной оценке параметров эконометрической модели довольно часто сталкиваются с проблемой взаимосвязи между объясняющими переменными. Если взаимосвязь довольно тесная, то оценка параметров модели может иметь большую погрешность. Такая взаимосвязь между объясняющими переменными называется мультиколлинеарностью. Мультиколлинеарность переменных приводит к смещению оценок параметров модели. Поэтому необходима проверка факторов на мультиколлинеарность. Наиболее простой формой проверки мультиколлинеарности является анализ корреляционной матрицы. Значение парных коэффициентов корреляции свидетельствует о том, связаны между собою переменные или нет. Но если в модели большее двух факторов, вопрос о мультиколлинеарности не может ограничиваться информацией, которая дает эта матрица. Более общая проверка предусматривает вычисление определителя матрицы R, ( Наиболее полное исследование мультиколлинеарности можно осуществить на основе алгоритма Феррара-Глаубера. Этот алгоритм включает три вида статистических критериев, на основе которых проверяется мультиколлинеарность всего массива переменных ( Пример 4. Затратына питание зависят от факторов:общие затраты, состав семьи и заработок. Надо исследовать наличие мультиколлинеарностипо алгоритму Феррара-Глаубера.
Решение. 1. Найдем корреляционную матрицу. Эта матрица симметричная. В нашем случае размера 3х3. Она имеет вид:
где
где Вычислим вспомогательную таблицу: Таблица 8 - Расчет элементов корреляционной матрицы
В нашем случае число испытаний
Рассчитаем средние квадратичные отклонения:
Рассчитанные значения подставим в формулу (9):
Для данной задачи корреляционная матрица (8) имеет вид:
Элементы этой матрицы характеризуют тесноту связи между факторами. В нашем случае 2. Найдем определитель
В нашем случае получим такие результаты:
В нашем случае число испытаний При степени свободы Если В нашем случае поскольку 3. Найдем обратную матрицу
где
Найденные алгебраические дополнения подставим в формулу (12):
4. Рассчитаем
где В нашем случае
Фактические значения статистики В нашем случае при уровне значимости 5. Найдем частные коэффициенты корреляции.
Частные коэффициенты корреляции характеризуют тесноту связи между двумя переменными при условии, что третья не влияет на эту связь. Частный коэффициент 6. Рассчитаем значения
Табличное значение Найденное фактическое значение 4 МНОЖЕСТВЕННАЯ РЕГРЕССИЯ Каждое явление в природе, экономике, общественной жизни, технике определяется комплексом причин. На уровень развития одного показателя могут влиять много факторов. Уровень влияния факторов на показатель может существенно различаться. Все эти закономерности следует учитывать во время проведения эконометрического анализа, прогнозирования и планирования. При существовании линейной зависимости объясняемой переменной (показателя)
Модель описывает совместное одновременное влияние факторов на показатель. Задача исследования состоит в оценке параметров регрессии Пример 5. Построить эконометрическую модель, которая характеризует зависимость между затратами на питание
Решение. Для построения линейной многофакторной модели (15)
где В соответствии с методом наименьших квадратов параметры
Вспомогательные вычисления удобно проводить в таблице: Таблица 9 - Расчет элементов системы (16)
В последней строке записывают суммы чисел в столбце. Можно найти средние для каждого показателя по формулам (17)-(19)
Система (16) для определения параметров регрессии имеет вид:
Из первого уравнения можно выразить
Тогда уравнение регрессии (15) имеет вид
Важным этапом регрессионного анализа является оценка практической значимости синтезированной модели. Проверку значимости модели проводят на основании показателей тесноты связи между признаками Множественный коэффициент корреляции
Для вычисления множественного коэффициента корреляции целесообразно рассчитать вспомогательную таблицу: Таблица 10 - Расчет элементов коэффициента
В соответствии с формулой (21) множественный коэффициент корреляции равняется
Чем более близок Коэффициент детерминации |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 261. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

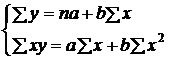




 – результативный показатель;
– результативный показатель;  – фактор времени;
– фактор времени; 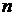 – количество наблюдений;
– количество наблюдений;  – параметры моделей.
– параметры моделей.



 – линейная модель.
– линейная модель.




 – параболическая модель.
– параболическая модель.



 – гиперболическая модель.
– гиперболическая модель. , (4)
, (4) – фактические значения показателя,
– фактические значения показателя,  – теоретические значения, найденные по уравнению.
– теоретические значения, найденные по уравнению. , потом находят среднее значение
, потом находят среднее значение  .
. .
. , (5)
, (5) – количество параметров в уравнении.
– количество параметров в уравнении. меньше.
меньше.



 ;
;  .
. ;
;  .
. . Поскольку
. Поскольку  ,
, не надо.
не надо.
 меньше всего.
меньше всего. (6)
(6)



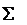 130,6
130,6
 .
. (приложение 1). Если
(приложение 1). Если  , то можно утверждать, что автокорреляция данных присутствует. В противоположном случае, то есть если
, то можно утверждать, что автокорреляция данных присутствует. В противоположном случае, то есть если  , то можно говорить об ее отсутствии.
, то можно говорить об ее отсутствии. . Поскольку
. Поскольку  автокорреляция присутствует.
автокорреляция присутствует.  , (7)
, (7) ,
,  – фактические значения показателя,
– фактические значения показателя,  – соответствующие теоретические значения показателя.
– соответствующие теоретические значения показателя. 







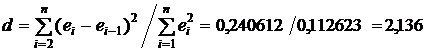
 и
и  (приложение 2). Здесь п – количество наблюдений, т – число факторов,
(приложение 2). Здесь п – количество наблюдений, т – число факторов,  – уровень значимости. В нашем случае критические значения статистики Дарбина-Уотсона при 5%-ном уровне значимости, то есть при
– уровень значимости. В нашем случае критические значения статистики Дарбина-Уотсона при 5%-ном уровне значимости, то есть при  и
и  .
.
 2
2 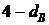
 4
4
 или
или  , то при выбранном уровне значимости не возможно сделать вывод о наличии или об отсутствии автокорреляции остатков, необходимо дальнейшее исследование.
, то при выбранном уровне значимости не возможно сделать вывод о наличии или об отсутствии автокорреляции остатков, необходимо дальнейшее исследование. ).
).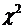 , хи-квадрат); каждой факторной переменной со всеми другими (F-статистика) и мультиколлинеарность каждой пары факторов (t-статистика). Все эти критерии при сравнении с их критическими значениями дают возможность сделать конкретные выводы относительно наличия или отсутствия мультиколлинеарности независимых переменных.
, хи-квадрат); каждой факторной переменной со всеми другими (F-статистика) и мультиколлинеарность каждой пары факторов (t-статистика). Все эти критерии при сравнении с их критическими значениями дают возможность сделать конкретные выводы относительно наличия или отсутствия мультиколлинеарности независимых переменных.



 , (8)
, (8) исчисляется по формуле
исчисляется по формуле , (9)
, (9)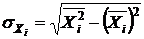 ,
,  ,
,  .
.








 равняется 10. Из таблицы 8 имеем:
равняется 10. Из таблицы 8 имеем:















 Между каждой парой факторов существует определенная связь.
Между каждой парой факторов существует определенная связь. корреляционной матрицы
корреляционной матрицы  по формуле (10):
по формуле (10):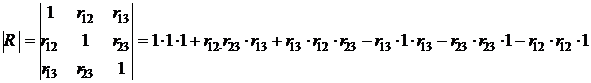 (10)
(10) Найдем
Найдем  (11)
(11) число факторов
число факторов  , поэтому формула (11), имеет вид:
, поэтому формула (11), имеет вид: 
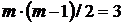 и уровне значимости
и уровне значимости  находим по таблице (приложение 3) критическое значение
находим по таблице (приложение 3) критическое значение 
 .
. , то мультиколлинеарность существует, в противном случае, то есть при
, то мультиколлинеарность существует, в противном случае, то есть при  мультиколлинеарность отсутствует.
мультиколлинеарность отсутствует.  ), то можем считать что мультиколлинеарность присутствует.
), то можем считать что мультиколлинеарность присутствует. к матрице
к матрице 
 , (12)
, (12) – алгебраическое дополнение к элементу
– алгебраическое дополнение к элементу 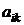 .
. 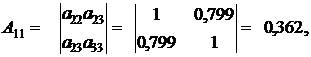

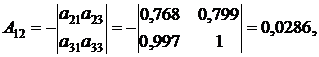





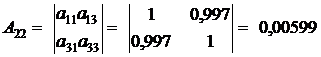

 - статистику по формуле (13):
- статистику по формуле (13): (13)
(13) – диагональные элементы матрицы
– диагональные элементы матрицы 
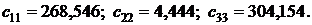 Эти значения подставим в формулу (13). Получим
Эти значения подставим в формулу (13). Получим ;
;  ;
; 
 сравниваются с табличными
сравниваются с табличными  (приложение 4) при
(приложение 4) при  и
и  степенях свободы и уровне значимости
степенях свободы и уровне значимости  . Если
. Если  , то переменная
, то переменная 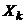 с другими не коррелирует. В противоположном случае, то есть если
с другими не коррелирует. В противоположном случае, то есть если  , то переменная
, то переменная  табличное значение критерия равняется
табличное значение критерия равняется  Поскольку все
Поскольку все  то можно сделать вывод, что переменные коррелируют между собой.
то можно сделать вывод, что переменные коррелируют между собой.
 приблизительно равен парному. Это свидетельствует о наличии мультиколлинеарности между переменными
приблизительно равен парному. Это свидетельствует о наличии мультиколлинеарности между переменными  .
. статистик:
статистик:
 статистики при 7 степенях свободы и уровне значимости 0,05 (приложение 5) равняется
статистики при 7 степенях свободы и уровне значимости 0,05 (приложение 5) равняется  . Если
. Если  , то между соответствующими переменными нет мультиколлинеарности. В противоположном случае, то есть если
, то между соответствующими переменными нет мультиколлинеарности. В противоположном случае, то есть если  , между соответствующими переменными имеется существенная мультиколлинеарность.
, между соответствующими переменными имеется существенная мультиколлинеарность. критерия больше табличного значения. Можно сделать вывод, что между переменными
критерия больше табличного значения. Можно сделать вывод, что между переменными  от нескольких объясняющих переменных (факторов)
от нескольких объясняющих переменных (факторов)  общее выражение уравнения множественной регрессии имеет вид (14):
общее выражение уравнения множественной регрессии имеет вид (14): (14)
(14) по результатам выборочных наблюдений над переменными, которые включены в модель. Построение модели проводят методом наименьших квадратов.
по результатам выборочных наблюдений над переменными, которые включены в модель. Построение модели проводят методом наименьших квадратов.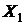 (условные денежные единицы) и составом семьи
(условные денежные единицы) и составом семьи 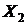 (количество членов семьи) на основе данных, которые приведенные в таблицы.
(количество членов семьи) на основе данных, которые приведенные в таблицы. , (15)
, (15) – теоретические значения показателя.
– теоретические значения показателя. ищут как решение системы линейных уравнений (16)
ищут как решение системы линейных уравнений (16) (16)
(16)




 ; (17)
; (17) ; (18)
; (18) . (19)
. (19)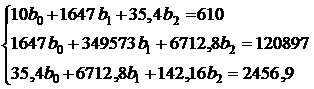
 и подставить во второе и третье уравнения:
и подставить во второе и третье уравнения:
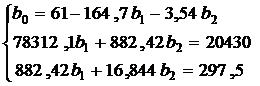


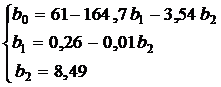

 . (20)
. (20) .
. равен коэффициенту корреляции между фактическими и теоретическими значениями объясняемой переменной. Его вычисляют по формуле (21)
равен коэффициенту корреляции между фактическими и теоретическими значениями объясняемой переменной. Его вычисляют по формуле (21) (21)
(21)
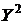


 610
610
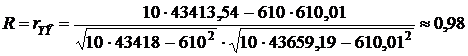 .
. равен квадрату множественного коэффициента корреляции. Он измеряет долю общей дисперсии относительно среднего
равен квадрату множественного коэффициента корреляции. Он измеряет долю общей дисперсии относительно среднего 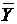 , которую можно объяснить регрессией.
, которую можно объяснить регрессией.