Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Проектирование систем в пространстве состояния ⇐ ПредыдущаяСтр 4 из 4
Метод синтеза по заданному расположению полюсов системы используется для непрерывных и дискретных систем автоматического управления. С расположением полюсов замкнутой системы управления непосредственно связаны многие динамические характеристики системы: время установления переходного процесса, показатели колебательности процесса, время достижения первого максимума и др. Метод синтеза непрерывной системы по заданному расположению полюсов применяется к моделям в форме пространства состояния:
где x – При использовании управления в форме обратной связи по состоянию Для обеспечения требуемых динамических характеристик замкнутой системы синтез управления выполняется в следующем порядке: 1. Исходя из требований к переходному процессу, выбирается расположение полюсов передаточной функции замкнутой системы на комплексной плоскости. 2. Рассчитываются значения коэффициентов обратных связей, при которых такое расположение полюсов достигается. Если пара матриц Если в непрерывной системе не все координаты вектора состояния доступны для непосредственного измерения, то можно использовать наблюдающее устройство, которое будет формировать оценки x переменных вектора состояния  Наблюдающее устройство описывается следующим дифференциальным уравнением: где Как правило, процессы в устройстве наблюдения должны протекать быстрее, чем процессы в управляемой системе, которые определяются собственными значениями матрицы Замена переменных вектора состояния Введем ошибку
Из этих уравнений следует, что так же как в дискретных системах (см. подразд. 2.2.7.4), можно независимо назначать полюсы наблюдателя и замкнутой системы управления, используя соответственно матрицы
Функции и команды. Для определения управляемости системы (3.5) функция U = ctrb(A,B) или U = ctrb(sys) формирует для пары матриц размером Пример 3.8. Рассмотрим задачу проверки управляемости линейной системы: >>A=[1 1; 4 –2]; >>B = [1 –1; 1 –1]; >>U= ctrb(A,B) U = 1 –1 2 –2 1 –1 2 –2 >>unco = length(A) – rank(U) % Количество неуправляемых мод unco = 1
Функция N = obsv(A,C) или N = obsv(sys) формирует матрицу наблюдаемости Метод модального синтеза реализован в функциях acker, place, reg и estim, входящих в состав пакета прикладных программ Control System Toolbox. Функция k = acker(A,B,p) предназначена для расчета вектора k коэффициентов обратных связей закона управления Желаемое расположение полюсов матрицы Этот метод в вычислительном отношении плохо обусловлен и приводит к значительным погрешностям, когда порядок динамической системы становится большим пяти и в случае плохо управляемых систем. Для более точных и надежных вычислений следует использовать функцию place, которая применима как в случае одномерных, так и в случае многомерных систем:
K = place(A,B,p)
где p – вектор желаемых положений полюсов замкнутой системы в комплексной плоскости, Замечание. Если для системы со скалярным управлением необходимо разместить два или более корней на одно и то же место, функция place не работает. В этом случае можно использовать функцию acker. Функции acker и place применимы как к непрерывным, так и к дискретным моделям динамических систем. Эти функции можно использовать для расчета вектора
L=place(A’,C’,p)
Функция est = estim(sys, L) формирует наблюдающее устройство в виде ss-объекта est для оценивания вектора переменных состояния объекта управления sys и для заданной матрицы коэффициентов обратных связей наблюдателя
Для дискретной модели наблюдатель описывается аналогичными уравнениями. Функция rsys = reg(sys,K,L) формирует динамический регулятор rsys для заданной в пространстве состояния модели объекта управления sys, матрицы
Для непрерывных систем регулятор описывается уравнениями (3.7). Этот регулятор должен быть объединен с объектом управления положительной обратной связью (рис. 3.14). Рис. 3.14 Пример 3.9. Рассмотрим непрерывную систему, описываемую дифференциальным уравнением
Вводя переменные состояния
Определим эту систему в MATLAB и произведем ее дискретизацию с периодом
»A=[0 1; 0 0]; »B = [0; 1]; »C = [1 0]; D=0; »sys = ss(A,B,C,D); »sysd=c2d(sys,0.44) a = x1 x2 x1 1 0.44 x2 0 1 b = u1 x1 0.0968 x2 0.44 c = x1 x2 y1 1 0 d = u1 y1 0 Sampling time: 0.44 Discrete-time model.
Зададим желаемое расположение корней исходя из требований к переходному процессу. Учитывая, что время регулирования в непрерывной системе определяется корнями характеристического уравнения
>>r =[0.697+0.224i 0.697–0.224i];
Вычислим вектор
>>K = place(sysd.A,sysd.B,r) place: ndigits= 15 K = 0.73267076128969 1.21395181379464
Используя управление в форме обратной связи по состоянию
>>A1=sysd.A-sysd.B*k >>B1=[0; 0]; >>sysd.a=A1; sysd.b=B1; >>x0=[1; 0]; >>initial(sysd,x0,15) Рис. 3.15
Предположим, что состояния системы недоступны непосредственному измерению. Используем для оценки состояния системы наблюдающее устройство. Потребуем, чтобы матрица
>>z=[0.748 0.75]; >>l=place(sysd.A',sysd.C',z) place: ndigits= 15 l = 0.51000000000000 0.14772727272727
По вычисленным векторам обратных связей K и L определим динамический регулятор и объединим его с объектом управления положительной обратной связью:
>>rsys=reg(sysd,k,l'); >>sysdr=feedback(sysd,rsys,1)
a = x1 x2 x3 x4 x1 1 0.44 -0.070923 -0.11751 x2 0 1 -0.32238 -0.53414 x3 0.51 0 0.41908 0.32249 x4 0.14773 0 -0.4701 0.46586
b = u1 x1 0.0968 x2 0.44 x3 0 x4 0 c = x1 x2 x3 x4 y1 1 0 0 0 d = u1 y1 0
Sampling time: 0.44 Discrete-time model.
Построим реакцию полученной замкнутой системы для дискретных моментов времени с помощью следующих операторов:
>>x0r=[1; 0; 0; 0]; >>initial(sysdr,x0r,15);
Переходный процесс по выходу для дискретных моментов времени при
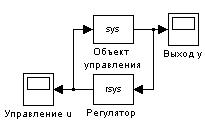
Рис. 3.16 Окончательное суждение о качестве переходных процессов исходной непрерывной системы (3.8), замкнутой кусочно-постоянным управлением, проводится по результатам ее моделирования с помощью пакета Simulink. Блок-схема замкнутой системы представлена на рис. 3.17, где модель непрерывного объекта управления и дискретного регулятора представлены с помощью определенных ранее LTI моделей sys и rsys. Выбор LTI моделей осуществляется с помощью окна Simulink Library Browser из раздела меню Control System Toolbox.
Рис. 3.17 Рис. 3.18 Рис. 3.19 Рис.3.20
После раскрытия LTI блока указывается его имя sys и вводятся начальные условия в строке Initial states, как показано на рис. 3.18. Аналогично задается блок rsys. Переходные процессы для выхода
КОНТРОЛЬНЫЕ ЗАДАНИЯ
В качестве контрольного задания предлагаются комплекты задач, решение которых опирается на теоретический материал и программные средства, изложенные в разд. 1-3 соответственно. Для каждой задачи предусмотрены варианты исходных данных, приведенные в таблицах.
4.1. Исходные данные и варианты Задача 4.1. Дана нелинейная замкнутая САУ, состоящая из нелинейности и линейной части (рис. 1.16 при Построить фазовый портрет, используя метод припасовывания, при передаточной функции Исходные данные приведены в табл. 4.1. Таблица 4.1
Задача 4.2. Используя метод гармонической линеаризации, определить условия существования автоколебаний в нелинейной САУ, изображенной на рис. 1.16 (при где Найти параметры автоколебаний и исследовать их устойчивость. Применить методы, основанные на критерии Михайлова и Найквиста (метод Гольдфарба). Исходные данные приведены в табл. 4.1. Коэффициенты гармонической линеаризации приведены в табл. 4.2.
Таблица 4.2
Коэффициент
Задача 4.3. Используя частотный критерий устойчивости Попова, исследовать абсолютную устойчивость состояния равновесия нелинейной САУ, приведенной на рис. 1.16 с передаточной функцией линейной части где Задача 4.4. Для импульсной системы, представленной на рис. 2.29, провести синтез корректирующего устройства по заданным показателям качества: время регулирования
Задача 4.5. Для импульсной системы с исходными данными задачи 4.4 построить дискретную модель в пространстве состояний (2.60) и провести синтез закона управления (2.64) в случае полных измерений вектора состояния и измерения рассогласования. Таблица 4.3
СПИСОК ЛИТЕРАТУРЫ
Основная
1. Теория автоматического управления. Ч. 2. Теория нелинейных и специальных систем автоматического управления /Под ред. А.А.Воронова. М.: Высшая школа, 1977. 2. Теория автоматического управления /Под ред. А.А.Воронова. М.: Высшая школа, 1986. 3. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. М.: Наука, 1975. 4. Попов Е.П. Теория нелинейных систем автоматического управления и регулирования. М.: Наука, 1983. 5. Красовский А.А., Поспелов Г.С. Основы автоматики и технической кибернетики. М.: Госэнергоиздат, 1962. 6. Шамриков Б.М. Основы теории цифровых систем управления. М.: Машиностроение, 1985. 7. Сборник задач по теории автоматического регулирования и управления /Под ред. В.А Бесекерского. М.: Наука, 1978.
Дополнительная
8. Иванов В.А., Медведев В.С., Чемоданов Б.К., Ющенко А.С. Математические основы теории автоматического регулирования. Т.1,2. М.: Высшая школа, 1977. 9. Цыпкин Я.З. Основы теории автоматических систем. М.: Наука, 1977. 10. Иванов В.А., Ющенко А.С. Теория дискретных систем автоматического управления. М.: Наука, 1983. 11. Куо Б. Теория и проектирование цифровых систем управления. М.: Машиностроение, 1986. 12. Острем К., Виттенмарк Б. Системы управления с ЭВМ. М.: Мир, 1987. 13. Сигалов Г.Г., Мадорский Л.С. Основы теории дискретных систем управления. Минск: Вышэйш. школа, 1973. 14. Стрейц В. Метод пространства состояний в теории дискретных линейных систем управления. М.: Наука, 1985. 15. Дроздов В. Н., Мирошник И. В., Скорубский В. И. Системы автоматического управления с микро-ЭВМ. Л.: Машиностроение, 1989. 16. Катковник В.Я., Полуэктов Р.А. Многомерные дискретные системы управления. М.: Наука, 1966. 17. Гаркушенко В.И., Земляков А.С., Файзутдинов Р.Н. Математические основы теории систем: Учебное пособие. Казань: Изд-во Казан. гос. техн. ун-та, 1999.
18. Потемкин В.Г. Система MATLAB 5 для студентов. М.: ДИАЛОГ-МИФИ, 1998. 19. Медведев В.С., Потемкин В.Г. Control System Toolbox. MATLAB 5 для студентов. М.: ДИАЛОГ-МИФИ, 1999. 20. Лазарев Ю.Ф. Matlab 5.x. Киев: Изд. группа BHV, 2000. 21. Говорухин В.Н. Цибулин В.Г. Введение в Maple. М.:Мир, 1997. 22. Теоретическая механика. Вывод и анализ уравнений движения на ЭВМ / В.Г. Веретенников, И.И.Карпов, А.П. Маркеев и др.; Под ред В.Г. Веретенникова. М.: Высшая школа, 1990.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 394. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 (3.5)
(3.5)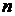 - вектор состояния; u –
- вектор состояния; u – 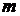 - вектор управления; y –
- вектор управления; y –  - вектор выходных переменных.
- вектор выходных переменных. динамика системы определяется уравнением
динамика системы определяется уравнением  . Полюса замкнутой системы в этом случае определяются как собственные значения матрицы
. Полюса замкнутой системы в этом случае определяются как собственные значения матрицы 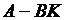 .
. управляема, то можно вычислить матрицу коэффициентов обратной связи
управляема, то можно вычислить матрицу коэффициентов обратной связи  , которая обеспечит любое желаемое расположение полюсов на комплексной плоскости. Этот метод называется методом модального синтеза или методом размещения полюсов.
, которая обеспечит любое желаемое расположение полюсов на комплексной плоскости. Этот метод называется методом модального синтеза или методом размещения полюсов. по известным векторам входов и измерений.
по известным векторам входов и измерений. , (3.6)
, (3.6)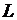 – неизвестная матрица постоянных коэффициентов. Полюсами наблюдателя (3.6) являются собственные значения матрицы
– неизвестная матрица постоянных коэффициентов. Полюсами наблюдателя (3.6) являются собственные значения матрицы  , которые могут быть назначены произвольно путем выбора коэффициентов обратных связей по переменным вектора состояния наблюдателя
, которые могут быть назначены произвольно путем выбора коэффициентов обратных связей по переменным вектора состояния наблюдателя  , т.е. путем задания элементов матрицы
, т.е. путем задания элементов матрицы  должна быть наблюдаемой.
должна быть наблюдаемой. . В результате получим уравнения, описывающие динамику наблюдателя и закон управления:
. В результате получим уравнения, описывающие динамику наблюдателя и закон управления: (3.7)
(3.7) . Уравнения динамики замкнутой системы управления в новых переменных состояния имеют вид
. Уравнения динамики замкнутой системы управления в новых переменных состояния имеют вид .
. ,
, 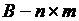 матрицу управляемости
матрицу управляемости ,
,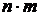 столбцов. Система является управляемой, если матрица управляемости имеет полный ранг. Если система (3.5) является неуправляемой, то количество неуправляемых мод равно разности порядка системы и ранга матрицы
столбцов. Система является управляемой, если матрица управляемости имеет полный ранг. Если система (3.5) является неуправляемой, то количество неуправляемых мод равно разности порядка системы и ранга матрицы  .
. для системы с матрицами
для системы с матрицами  . Размерность матрицы
. Размерность матрицы  :
:  строк и n столбцов. Система наблюдаема, если матрица
строк и n столбцов. Система наблюдаема, если матрица  для заданной одномерной системы вида
для заданной одномерной системы вида .
.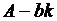 замкнутой системы задается вектором p.
замкнутой системы задается вектором p.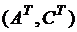 . Например:
. Например: объекта управления в соответствии с уравнениями:
объекта управления в соответствии с уравнениями:

 . (3.8)
. (3.8) , эту систему можно записать в виде модели пространства состояния
, эту систему можно записать в виде модели пространства состояния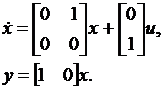
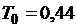 с:
с: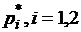 , желаемые корни замкнутой дискретной системы найдем по формулам
, желаемые корни замкнутой дискретной системы найдем по формулам  ,
,  . Полагая
. Полагая 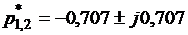 при
при 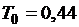 найдем вектор желаемого расположения корней:
найдем вектор желаемого расположения корней: коэффициентов обратных связей по переменным состояния:
коэффициентов обратных связей по переменным состояния: для дискретных моментов времени (рис. 3.15):
для дискретных моментов времени (рис. 3.15):
 ,
,  , для которых найдем вектор коэффициентов
, для которых найдем вектор коэффициентов 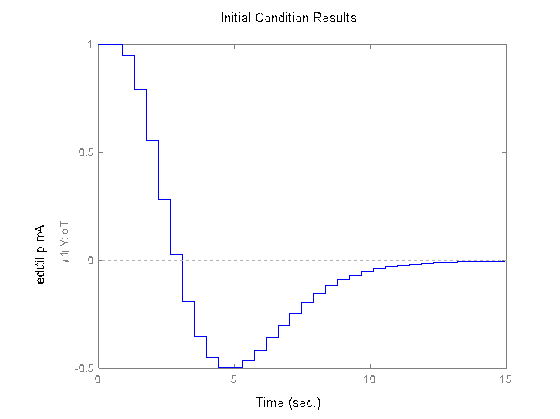



 и кусочно-постоянного управления
и кусочно-постоянного управления  приведены на рис. 3.19 и рис.3.20 соответственно. Из переходных процессов рис. 3.16 и рис. 3.19 следует, что в замкнутой системе отсутствуют скрытые колебания между моментами квантования с периодом дискретности
приведены на рис. 3.19 и рис.3.20 соответственно. Из переходных процессов рис. 3.16 и рис. 3.19 следует, что в замкнутой системе отсутствуют скрытые колебания между моментами квантования с периодом дискретности  ).
).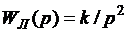 и соответствующей нелинейности.
и соответствующей нелинейности. (рис.1.5)
(рис.1.5)
 (рис.1.6)
(рис.1.6)
 (рис.1.2)
(рис.1.2)

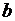
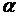
 ,
, ;
; 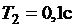 ;
; 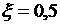 при заданной нелинейности из табл. 4.1.
при заданной нелинейности из табл. 4.1.

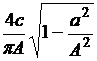 при
при 
 при
при  при
при 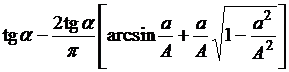 при
при  для всех приведенных нелинейностей.
для всех приведенных нелинейностей. ,
, с,
с,  с,
с,  с, перерегулирование
с, перерегулирование  ; построить переходный процесс по выходу. На входе действует сигнал
; построить переходный процесс по выходу. На входе действует сигнал  ; передаточная функция фиксатора нулевого порядка имеет вид
; передаточная функция фиксатора нулевого порядка имеет вид  , где
, где  с; вид передаточной функции непрерывного объекта управления представлен в табл. 4.3.
с; вид передаточной функции непрерывного объекта управления представлен в табл. 4.3.