Использование символьных преобразований для исследования систем управления

При исследовании систем управления стандартными средствами MATLAB результат получается в численной форме. Однако при проведении исследований часто бывает важно исследовать результат в аналитической (символьной) форме.

3.4.1. Использование символьных преобразований в среде MATLAB.

В системе MATLAB символьные вычисления реализуются средствами Symbolic Toolbox. В состав пакета включено ядро системы символьных вычислений MAPLE V, разработанное фирмой Waterloo MAPLE Software (Canada).

Пакет Symbolic добавил системе MATLAB существенно новое свойство – возможность выполнения символьных вычислений и преобразований, которые ранее были доступны только в системах принципиально иного класса, относящихся к компьютерной алгебре. Применяя Symbolic Toolbox, можно легко в единой среде выполнять как численные, так и символьные вычисления без ущерба для скорости и точности вычислений.

Помимо типовых аналитических вычислений (символьное дифференцирование и интегрирование, упрощение математических выражений и т.п.) пакет Symbolic позволяет выполнять арифметические выражения с произвольной точностью.

Базовые символьные операции. Переменные среды MATLAB не определены и обычно задаются как числовые или матричные. Поэтому в первую очередь необходимо создать специальные символьные переменные.

В простейшем случае их можно определить как строковые переменные, то есть заключить в апострофы:

Пример:

>>sin('x')^2+cos('x')^2

ans =

1

Для объявления символьной переменной используется оператор sym,     например:

x=sym('x') – создание символьной переменной .

Чаще всего, для задания символьных переменных используется команда syms arg1 arg2 … – короткая запись последовательности функций sym: arg1=sym('arg1'); arg2=sym('arg2'); …

Преобразования объектов. Для преобразования объектов между символьной и числовой формами представления в MATLAB используются следующие команды:

r=double(S) – преобразование символьного объекта S в число (или массив) удвоенной точности;

r=poly2sym(c) – возвращение символьного представления полинома, коэффициенты которого записаны в векторе с.

c=sym2poly(r) – обратное преобразование символьного полинома в вектор-строку коэффициентов c.

Аналитические преобразования. Одни из наиболее часто используемых команд в системах компьютерной алгебры – это команды для выполнения символьных преобразований. Приведем их список:

r=simplify(s) – упрощает каждый элемент символьного массива s;

r=expand(s) – раскрывает каждый элемент символьного массива s.

r=factor(s) – разлагает полиномы на множители;

r=collect(s) – собирает однородные члены по степеням переменной х;

r=simple(s) – упрощает символьное выражение (выводит его в самой короткой форме).

[N, D] = numden(A) – преобразовывает каждый элемент символьного массива А к рациональной форме в виде отношения двух неприводимых полиномов с целыми коэффициентами; N и D – символьные массивы числителей и знаменателей элементов массивов.

Пример. 3.2. Символьное преобразование передаточных функций.

Рассмотрим разомкнутую систему с передаточной функцией

                                  .

Определим передаточную функцию (используя команды Symbolic toolbox):

>>Gs=sym('1')/sym('(s+1)*(5*s+1)')

Gs=

1/(s+1)/(5*s+1)

Исследуем реакцию на единичный скачок объекта с единичной обратной связью без регулятора. Передаточные функции замкнутой системы по команде и ошибке:

                и .

Определим их в MATLAB:

>>Gc=simplify(Gs/(sym('1')+Gs))

Gc=

1/(2 + 5*s^2 + 6*s)

>>Ge=simplify(sym('1')/(sym('1')+Gs))

Ge=

(s+1)*(5*s+1)/(2 + 5*s^2 + 6*s)

Для исследования реакции системы преобразуем символьные передаточные функции сначала в вектор-строки, а затем в объекты LTI:

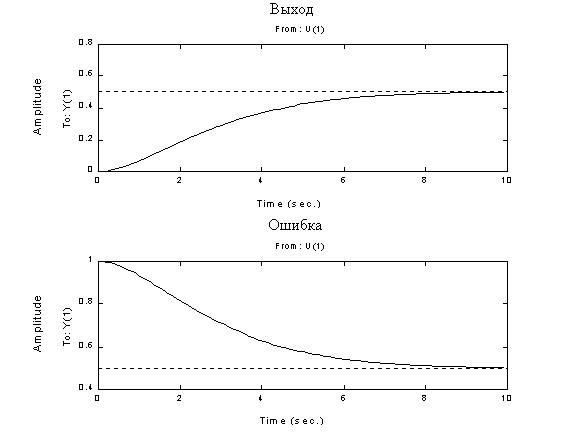
% Выделяем числители и знаменатели

>>[NGc, DGc] = numden(Gc);

>>[NGе, DGе] = numden(Gc);

% Преобразуем символьные объекты в переменные типа ”передаточная функция”

>>numGc = sym2poly(expand(NGc))

>>denGc = sym2poly(expand(DGc))

>>Gclti=tf(numGc,denGc)

>>numGe = sym2poly(expand(NGe))

>>denGe = sym2poly(expand(DGe))

>>Gelti=tf(numGe,denGe)

% Построим переходные процессы

>>subplot(211), step(Gclti), title('Выход'), grid on

>>subplot(212), step(Gelti), title('Ошибка'), grid on

Рис. 3.2

В результате получим графики переходных процессов (рис.3.2).

3.4.2. Использование пакета MAPLE V для исследования устойчи­вости систем управления. Приведем краткое описание системы MAPLE, необходимое для понимания дальнейшего материала.

Работа в MAPLE происходит в режиме сессии – пользователь вводит предложения (команды, выражения и процедуры), которые воспринимаются и интерпретируются MAPLE. При этом документ MAPLE разделяется на три части: область ввода (Input Region), которая состоит из набираемых предложений, область вывода (Output Region) и текстовые комментарии (Text Region). Эти области в документах MAPLE выделяются различными цветами. Область вывода может включать как результаты выполнения математических операций в виде формул, так и графические образы.

Символом приглашения системы к вводу команд является “>”. Каждая команда должна завершаться разделителем: точкой с запятой (;) или двоеточием (:). При построении выражений, как и в алгоритмическом языке Паскаль, знаком присваивания является “:=”.

Переменные в MAPLE не объявляются, а определяются при присваивании им значений исходя из контекста. По умолчанию переменная считается скалярной и имеющий строковый тип, фактически это математическая переменная.

Для задания массивов их нужно объявить командой array, например

> A := array(1..2,1..2, [[a,b],[c,d]]);

Здесь для указания размерности массива использован знак диапазона: две идущие подряд точки. Данные в массивах задаются в виде списков. Списки – это упорядоченные последовательности данных, заключенные в квадратные скобки. В данном случае каждая строка массива задана в виде списка – [a,b] и [c,d]. Сам массив также определен в виде списка, состоящего из подсписков.

Для описания матрицы в MAPLE используется двухмерный массив, для вектора – одномерный массив, индексы которых начинаются с единицы. Для задания матриц и векторов можно использовать команду array.

Для описания векторов и матриц можно также использовать команды пакета линейной алгебры linalg.

Команда описания матрицы из пакета linalg имеет вид:

> matrix(n,m,[val1, val2, … ])

Здесь n – число строк матрицы; m – число столбцов; val1, val2, … – значения элементов матрицы.

Для описания вектора используется команда

> vector(n,[val1, val2, … ])

где n – размерность вектора; val1, val2, … – значения элементов. Если опущен параметр размерности, то размерность вектора определяется числом его элементов.

Наиболее часто используемые команды MAPLE – это операции аналитического преобразования формул: simplify(f) – упрощение выражения f;

expand(f) – раскрытие скобок в выражении f; factor(f) – разложение на множители; collect(expr,var) – приведение подобных членов в выражении expr относительно переменной var.

Команда subs(old=new, expr) выполняет подстановку выражения new вместо old в выражение expr.

Для нормализации дроби (сокращения общих множителей и приведения к виду числитель/знаменатель) используется команда normal(expr). Команды numer(expr) и denom(expr) выделяют соответственно числитель и знаменатель из рациональной дроби expr. Команда coeffs(poly,var)        вычисляет коэффициенты полинома poly при переменной var; результат операции – переменная типа "список" (list), содержащая неупорядоченные коэффициенты.

Для выделения вещественной и мнимой частей выражения expr используются команды соответственно Re(expr) и Im(expr).

Команда diff(expr, var) выполняет дифференцирование выражения expr по переменной var.

Для аналитического решения уравнений используется команда solve(eqns,vars), где eqns – уравнение или система уравнений;

vars – переменная или группа уравнений в фигурных скобках.

Исследование устойчивости линейных систем. Рассмотрим методы и алгоритмы анализа устойчивости линейных систем с использованием системы аналитических вычислений (компьютерной алгебры) MAPLE V.

Пример 3.3. Рассмотрим задачу определения характеристического уравнения для системы спутник-стабилизатор в центральном ньютоновском поле тяготения на круговой орбите со скоростью v. Малые колебания системы спутник-стабилизатор в плоскости орбиты в окрестности положения равновесия описываются системой уравнений

                 (3.3)

Здесь a₁, a₂ – углы, определяющие отклонения спутника и стабилизатора от направления радиус-вектора R центра системы;  – главные центральные моменты инерции тел, величины  и  характеризуют вязкость и упругость подвеса.

Определим матрицу системы в MAPLE:

> А = matrix(4,4,[[0,0,1,0], [0,0,0,1], [-(3*(A1-C1)+k2)/B1, k2/B1, -k1/B1, k1/B1], [k2/B2, -(3*(A2-C2)+k2)/B2, (k1/B2), (-k1/B2)];

      .

Для вычисления характеристического многочлена матрицы A относительно переменной lambda используем команду charpoly:

> pol:=charpoly(A,lambda);

pol:=(l⁴ B1 B2+l³ B1 k1 + l³ k1 B2 + 3 A2 l² B1 +

3l A2 k1 – 3C2 l² B1 –3l C2 k1 + k2 l² B1 +

3 k1 A1 – 3k1 C1 – k2 l B1)/(B1 B2)

> pol:=collect(pol,lambda);

Определим численные значения параметров:

> A1:=80; B1:=100; C1:=20; k1:=20;

> A2:=90; B1:=120; C1:=60; k1:=20;

> pol;

Для исследования устойчивости по уравнениям первого приближения необходимо исследовать знаки вещественных корней характеристического уравнения.

Необходимые и достаточные условия, при которых характеристическое уравнение системы имеет все корни с отрицательными вещественными частями, даются критерием Рауса – Гурвица.

Пример 3.4. Определить, является ли нулевое решение системы разностных уравнений

асимптотически устойчивым.

Определим матрицу системы в среде MAPLE:

> a:=array(1..3,1..3,[[0.1,0,0.2],[0.4,0.2,0.5],

[-0.1,-0.2,0.3]]);

                            [.1 0 .2]

                       [           ]

                  a := [.4 .2 .5]

                       [               ]

                       [-.1 -.2 .3]

Характеристический полином

> charp:=charpoly(a,x);

                       3  2

             charp := x - .6 x + .23 x - .004

Делаем замену переменной

> x:=(1+y)/(1-y);

                                1 + y

                         x := -----

                              1 - y

> pol1:=subs(x=(1+y)/(1-y),charp);

           3        2

    (1 + y)  (1 + y)   1 + y

pol1 := -------- - .6 -------- + .23 ----- - .004

            3        2  1 - y

    (1 - y)  (1 - y)

> pol2:=normal(pol1);

                               2     3

       .626 + 2.182 y + 3.358 y + 1.834 y

pol2 := - ------------------------------------

                        3

                 (-1 + y)

> nm:=-numer(pol2);

                           2     3

nm := .626 + 2.182 y + 3.358 y + 1.834 y

> cf:=coeffs(nm,y);

cf := 2.182, 3.358, 1.834, .626

Все коэффициенты характеристического полинома больше нуля. Вычислим определитель Гурвица :

> delta:=cf[2]*cf[1]-cf[3]*cf[4];

                     delta := 6.179072

Так как определитель тоже положителен, система устойчива.