
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Необходимое условие относительного экстремумаОбозначим через Понятно, что
тогда условия
будут необходимыми и достаточными условиями минимума и максимума, соответственно. Однако, эти условия не конструктивны. Для получения более эффективных условий вводится понятие первой вариации функционала. Для этого представим приращение функционала
где Тогда при достаточно малых Из выражения (1.10) следует, что необходимым условием минимума или максимума (экстремума) функционала является условие
Для доказательства предположим, что кривая Условие (1.11) еще называют условием стационарности. Поскольку оно является необходимым условием экстремума, ему должны удовлетворять все кривые, доставляющие и минимум, и максимум функционалу 
Основная лемма вариационного исчисления Лемма. Пусть
где
Поскольку
В этом случае
что противоречит условию (1.12) и доказывает лемму.
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 235. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 искомую экстремаль. Тогда любую другую функцию из рассматриваемого класса можно представить в виде
искомую экстремаль. Тогда любую другую функцию из рассматриваемого класса можно представить в виде 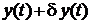 , где
, где 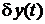 - вариация функции. При этом, если
- вариация функции. При этом, если 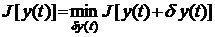 ,
,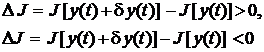 (1.9)
(1.9)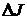 в виде
в виде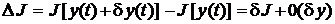 , (1.10)
, (1.10)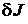 - линейная относительно
- линейная относительно 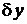 часть приращения,
часть приращения, 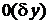 содержит величины более высокого порядка малости, чем
содержит величины более высокого порядка малости, чем 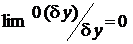 при
при  .
.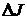 будет определяться знаком первой вариации
будет определяться знаком первой вариации  (1.11)
(1.11) . Это означает, что при любых
. Это означает, что при любых 
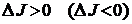 . Если теперь предположить, что условие (1.11) неверно, то в силу линейности
. Если теперь предположить, что условие (1.11) неверно, то в силу линейности 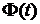 - заданная непрерывная функция, удовлетворяющая уравнению
- заданная непрерывная функция, удовлетворяющая уравнению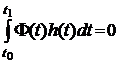 , (1.12)
, (1.12)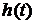 - любая непрерывная функция, то
- любая непрерывная функция, то 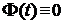 .
.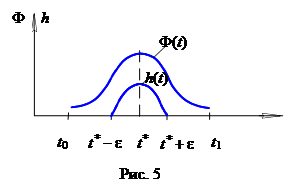 Доказательство. Предположим, что условие
Доказательство. Предположим, что условие  , в которой
, в которой 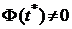 . Для определенности положим, что
. Для определенности положим, что  . Тогда в силу непрерывности функции
. Тогда в силу непрерывности функции 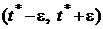 , где
, где 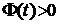 .
.
 ,
,