
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
В чем суть и содержание метода имитации с использованием модели случайных входов? ⇐ ПредыдущаяСтр 2 из 2
Принципы построения имитационных моделирующих Алгоритмов Имитационная модель является, как правило, динамической моделью, отражающей последовательность протекания элементарных процессов и взаимодействие отдельных элементов по оси «модельного» времени tM. Процесс функционирования объекта в течение некоторого интервала времени Т можно представить как случайную последовательность дискретных моментов времени При построении формализованной схемы процесса должно выполняться следующее рекуррентное правило: событие, происходящее в момент времени Реализация этого правила может проводиться различными способами. 1. Повременное моделирование с детерминированным шагом («принцип Способ моделирования с детерминированным шагом состоит из совокупности многократно повторяющихся действий: 
«Принцип 2. Современное моделирование со случайным шагом (моделирование по «особым» состояниям). При рассмотрении большинства сложных систем можно обнаружить два типа состояний системы: 1) обычные (неособые) состояния, в которых система находится большую част времени, и 2) особые состояния, характерные для системы в некоторые моменты времени, совпадающие с моментами поступления в систему воздействий из окружения, выхода одной из характеристик системы на границу области существования и т.д. Например, станок работает – обычное состояние, станок сломан – особое состояние. Любое скачкообразное изменение состояния объекта может рассматриваться при моделировании как переход в новое «особое» состояние. Повременное моделирование со случайным шагом (от события к событию) заключается в том, что моделирующий алгоритм осматривает модели элементов системы только в такие моменты времени, когда состояние исследуемой системы меняется. В те моменты времени, когда модель какого либо элемента системы должна менять состояние, происходит осмотр модели именно этого элемента и с учетом взаимосвязей элементов корректируется состояние модели всей системы. Длительность шага 3. Позаявочный способ. При моделировании процессов обработки последовательно идущих заявок иногда удобно строить моделирующие алгоритмы позаявочным способом, при котором прослеживается прохождение каждой заявки (детали, носителя информации) от ее входа в систему и до выхода ее из системы. После этого алгоритм предусматривает переход к рассмотрению следующей заявки. Такого рода моделирующие алгоритмы весьма экономичны и не требуют специальных мер для учета особых состояний системы. Однако этот способ может использоваться только в простых моделях в случаях последовательных заявок, не опережающих друг друга, т.к. в противном случае становится весьма затруднительным учет взаимодействия заявок, поступающих в систему. Моделирующие алгоритмы могут сроиться на нескольких принципах одновременно. Например, общая структура моделирующего алгоритма базируется на принципе особых состояний, а между особыми состояниями для всех заявок реализуется позаявочный способ. Структура моделирующего алгоритма, как показывает практика, имеет специфику, связанную с узкими классами конкретных типов систем и задач, для решений которых предназначена модель.
Модели случайных входов Создавая стохастическую имитационную модель, всегда приходится решать, следует ли в модели использовать имеющиеся эмпирические значения входных стохастических факторов непосредственно или целесообразно использовать их теоретико-вероятностные или частотные распределения. Непосредственное использование имеющихся статистических данных предполагает запись в память ЭВМ и выборку их из памяти определенным образом, обеспечивающим «чистоту» статистического эксперимента. В общем случае применение теоретических частотных или вероятностных распределений с учетом требований к машинному времени и памяти более эффективно, чем использование табличных данных для получения значений случайных факторов, необходимых в работе с моделью. Кроме того, использование необработанных эмпирических данных означает, что имитируется только прошлое. Возможными будут считаться только те события, которые уже происходили. В связи с этим на практике в большинстве случаев эмпирические данные обрабатываются для получения наиболее близкого к ним теоретического закона распределения данной случайной величины и дальнейшего воспроизведения этого закона в процессе моделирования. Для введения в моделирующий алгоритм случайных факторов используются специальные модели имитации случайных величин и событий. Эти модели являются основополагающими в статистическом моделировании, так как практически все остальные действия сводятся к преобразованию полученных случайных чисел по соответствующим правилам. В качестве исходной последовательности для получения случайных чисел с любым законом распределения либо для моделирования случайных событий используются случайные числа, равномерно распределенные в интервале (0 – 1). Наиболее распространенным способом получения таких чисел является программный. К настоящему времени создано большое количество разнообразных программ получения случайных чисел. В программное обеспечение современных ЭВМ входят стандартные программы генерирования случайных чисел, равномерно распределенных в интервале (0 – 1). Преобразование случайных чисел с равномерным законом распределения в случайные числа с заданным (в общем случае произвольным) законом распределения базируется на теореме: если случайная величина yi имеет плотность распределения f(y), то случайная величина
является равномерно распределенной в интервале (0-1). Решение уравнения (4.1) относительно yi дает возможность получить искомое случайное число (рис. 4.2).
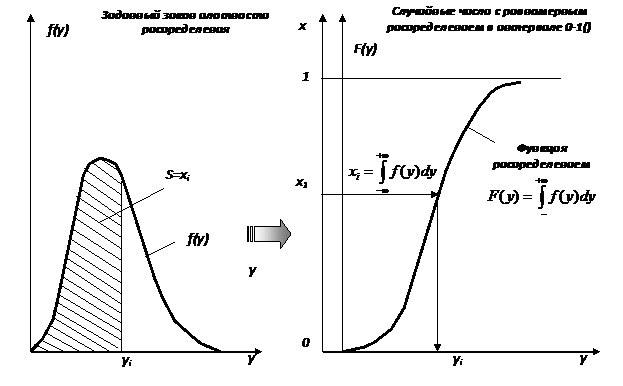
Рис. 4.2. Получение случайных чисел решением интегрального уравнения Точное решение интегрального уравнения (4.1) возможно только для ряда относительно простых законов распределения, например: 1. Равномерное распределение с параметрами
2. Показательное распределение с параметрами
Но так как случайная величина (1-xi) также имеет равномерное распределение в интервале (1 – 0), справедливо
Однако в большинстве практически важных случаях уравнение (4.1) относительно yi точно не решается, поэтому на практике большое развитие получили приближенные методы.
|
||||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 623. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
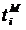 . В каждый из этих моментов происходят изменения состояний элементов объекта, а в промежутке между ними никаких изменений состояния не происходит.
. В каждый из этих моментов происходят изменения состояний элементов объекта, а в промежутке между ними никаких изменений состояния не происходит.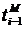 . В противном случае результат моделирования может быть неверным.
. В противном случае результат моделирования может быть неверным.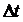 ») при повременном моделировании с детерминированным шагом алгоритм одновременно просматривает все элементы системы через достаточно малые промежутки времени (шаг моделирования) и анализирует все возможные взаимодействия между элементами. Для этого определяется минимальный интервал времени, в течении которого не может измениться состояние ни одного из элементов системы; детализированная величина
») при повременном моделировании с детерминированным шагом алгоритм одновременно просматривает все элементы системы через достаточно малые промежутки времени (шаг моделирования) и анализирует все возможные взаимодействия между элементами. Для этого определяется минимальный интервал времени, в течении которого не может измениться состояние ни одного из элементов системы; детализированная величина 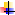 на i-м шаге в момент ti просматриваются все элементы объекта и определяется, какие из них изменяют свое состояние в этот момент;
на i-м шаге в момент ti просматриваются все элементы объекта и определяется, какие из них изменяют свое состояние в этот момент;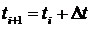 .
.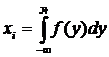 (4.1)
(4.1)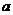 и
и 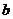 :
: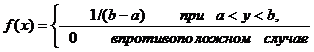 ;
;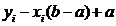 .
.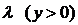 :
: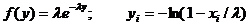 .
.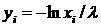 .
.