
Студопедия
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
|
Однородные дифференциальные уравнения первого порядка.
Функция ( f,y ) , наз однородной ф-ей степени m, если для всех x и у из обл. опред . D(f) выполняются при любых значения параметра  f( f(  x, x, 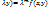 Дифф-ое ур-ие вида:M(x,y)dy+N(x,y)dx=0 (1)наз. Однородным если ф-ияM ,N однородный одной и той же степени.Однородноеур-ие (1) можно привести к ур-ию с разделяющимися переменными ,а зн может быть проинтегрирована в квадратах. В ведем в рассмотрение новую ф-июy=xu (2) и подставим в ур-ие (1) M(x,xu)d(xu)+N(x,xu)dx=0 , тогда получаемxM(1,u)du+(uM(1,u)+N(1,u)dx)=0—данное ур-ие относиться к классу с разделяющими переменными ,разделим : Дифф-ое ур-ие вида:M(x,y)dy+N(x,y)dx=0 (1)наз. Однородным если ф-ияM ,N однородный одной и той же степени.Однородноеур-ие (1) можно привести к ур-ию с разделяющимися переменными ,а зн может быть проинтегрирована в квадратах. В ведем в рассмотрение новую ф-июy=xu (2) и подставим в ур-ие (1) M(x,xu)d(xu)+N(x,xu)dx=0 , тогда получаемxM(1,u)du+(uM(1,u)+N(1,u)dx)=0—данное ур-ие относиться к классу с разделяющими переменными ,разделим :  du+dx/x=0---ур-ие с разделенными переменными . Его общий интеграл: du+dx/x=0---ур-ие с разделенными переменными . Его общий интеграл: 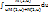 + + 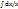 = =  (3) (3)
ln  - ln - ln  + + 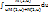
x=Cexp ( 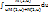 )—(4) )—(4)
Т.о (4) есть интегральное ур-ие (3).Заметим ,что при разделение переменных могут быть потеряны решения вида u=a, где а –корень ур-ия :uM(1,u)+N(1,u)=0
Выполняя обратную замену согласно(2) подставим (4) вместо u=x/y, получим общее интегральное ур-ие(1).В ур-ие (1) выполняем следующие преобразования :M(x, x  )dy+N(x, x )dy+N(x, x  )dx=0 )dx=0
dy/dx= 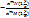 y’=- y’=- 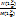 , y’(x)=f(y/x) (5) Т.о доказали ,что однородное дифф. ур-ие можно привести к виду (5).Ур-ие вида : y(x)=f( , y’(x)=f(y/x) (5) Т.о доказали ,что однородное дифф. ур-ие можно привести к виду (5).Ур-ие вида : y(x)=f( 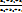 )—(6) ,для которых выражение )—(6) ,для которых выражение 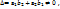 можно привести к однородному ур-ию: можно привести к однородному ур-ию: 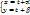 где где  - координаты точки пересечения прямых :u= - координаты точки пересечения прямых :u= 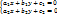 , то есть решим системы .Если , то есть решим системы .Если  то прямые параллельны (или совпадают) ,поэтому введя в рассмотрения новую ф-ю u , по формуле: u= то прямые параллельны (или совпадают) ,поэтому введя в рассмотрения новую ф-ю u , по формуле: u=  или u= или u= 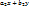 , ур-ие (6) приведем к ур-ию с разделяющимися переменными .Ур-ие (1) будет наз. обобщенным однородным ,если удается подобрать такое число , ур-ие (6) приведем к ур-ию с разделяющимися переменными .Ур-ие (1) будет наз. обобщенным однородным ,если удается подобрать такое число  ,что левая часть ,этого ур-ия становится однородной функцией некоторой степени m относительно x,y,dx,dy при этом система х- величина измерения 1,у- величина измерения ,что левая часть ,этого ур-ия становится однородной функцией некоторой степени m относительно x,y,dx,dy при этом система х- величина измерения 1,у- величина измерения  ,dx- измерение 0, dy- величина измерения ,dx- измерение 0, dy- величина измерения 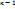 .Тогда .Тогда 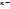 наз величиной неоднородности .Обобщенное однородное ур-ие сводится к ур-ию с разделяющимися переменными с заменой :y=u наз величиной неоднородности .Обобщенное однородное ур-ие сводится к ур-ию с разделяющимися переменными с заменой :y=u  . .
7. Линейные дифференциальные уравнения первого порядка.y'(x)=a(x)y+b(x)—(1) ур-ие линейное диффур-ие 1-ого порядка.Vx 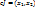 y'(x)=a(x)y—(2)-однородное ур-иет.о ,если b(x) y'(x)=a(x)y—(2)-однородное ур-иет.о ,если b(x) 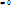 ,то (1) наз. неоднородным (1),(2) наз. соответственно. Заметим ,что (2) можно отнести к классу с разделяющимися переменными .В связи с этим можно интегрировать 2 способом ур-ие (1):1. Метод Лагранжа : ,то (1) наз. неоднородным (1),(2) наз. соответственно. Заметим ,что (2) можно отнести к классу с разделяющимися переменными .В связи с этим можно интегрировать 2 способом ур-ие (1):1. Метод Лагранжа :
При решении в начале вместо неоднородного (1) находим решение однородного(2):
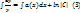 , , 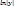 = = 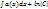 (4) (4)
2.Ур-ие содержащее независемой переменной х,т.е имеет вид:F(y,y’,…, 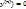 —(5).Порядок данного ур-ия можем понизить на единицу ,введя в рассмотрение функцию z=y, причем будет новой функцией z=z(y).Чтобы выполнить данную замену в ур-ие (5)необходимо выразить через саму ф-июz и ее производную :z’=dz/dy, тогда —(5).Порядок данного ур-ия можем понизить на единицу ,введя в рассмотрение функцию z=y, причем будет новой функцией z=z(y).Чтобы выполнить данную замену в ур-ие (5)необходимо выразить через саму ф-июz и ее производную :z’=dz/dy, тогда
y'’=  ( ( 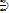 = = 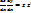
y’’= 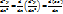 = = 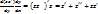 как видим из вычисленной производной ф-ииу к-го порядка выражается через производные ф-ииz порядков к-1 и ниже, что приводит при подставке и в ур-ие (5) понижение порядка на единицу .В частности если ур-ие (5) ур-ие 2-го порядка ,то указанная замена приводит его к ур-ию 1-го порядка т.о. с помощью указанной заменой ,ур-ие (5) приводится к виду: как видим из вычисленной производной ф-ииу к-го порядка выражается через производные ф-ииz порядков к-1 и ниже, что приводит при подставке и в ур-ие (5) понижение порядка на единицу .В частности если ур-ие (5) ур-ие 2-го порядка ,то указанная замена приводит его к ур-ию 1-го порядка т.о. с помощью указанной заменой ,ур-ие (5) приводится к виду:  =(y,z, =(y,z, 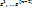 ) его общее решение зависит от z=z(y, ) его общее решение зависит от z=z(y, 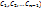 . Учитывая замену ,получим ур-ие с разделяющимися переменными ,метод интегрирования который рассматривали ранние. . Учитывая замену ,получим ур-ие с разделяющимися переменными ,метод интегрирования который рассматривали ранние.
3. F(х,y,y’,…, 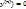 —(6) является производной некоторого дифф-го выражения (n-1)- го порядка Ф(х,y,y’,…, —(6) является производной некоторого дифф-го выражения (n-1)- го порядка Ф(х,y,y’,…, 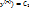 --(7)представляет собой дифф-оеур-ие порядка (n-1),т.е. понизили порядок ур-ия (6)на единицу. Такое выражение (7)наз. 1-ым интегралом ур-ия (6). --(7)представляет собой дифф-оеур-ие порядка (n-1),т.е. понизили порядок ур-ия (6)на единицу. Такое выражение (7)наз. 1-ым интегралом ур-ия (6).
Определение:Дифф-оеур-ие (n-1) –го порядка ,содержащее одну произвольную константу эквивалентная данному дифф-муур-июn-го порядка будем наз. 1-м интегралом этого дифф-гоур-ия порядка n.
8. Уравнения в полных дифференциалах и приводящиеся к ним. Использование нтегрирующего множителя.
Ур-ие полных дифф-ов:
Пусть дифф-ал выражения: M(x,y)dx+N(x,y)dy-- является полным дифф-ом некоторой ф-ииu=(x,y) , тогда M(x,y)dx+N(x,y)dy=0 –(2) ур-ие в полном дифф-але ,для нахождения полного интеграла (2) достаточно подставить (1)в (2).
Получим: du=0àu(x,y)=c , где с—произвольная константа .
Теорема 1:
(2) будет ур-ие в полном дифф-ле тогда и только тогда, когда на обл. заданного ур-ия выполняется  —(4’) —(4’)
Докозательство :Если (2) есть в полномдифф-м то справ.(1)
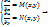 (5’) , (5’) , 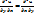 , , 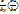 = = 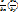
Подставим в соотношение (5’) получим (4’).Если выполнится (1),то (2)—ура-ие в полномдифф-ле. Теорема доказана!
M(x,y)dx+N(x,y)dy=0—(1) ,
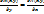 --(4) --(4)
du=  dx+ dx+  dy= M(x,y)dx+N(x,y)dy , dy= M(x,y)dx+N(x,y)dy , 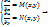 (5). (5).
Нахождение из системы (5) :u(x,y)= 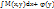 --(6) , --(6) ,  ( ( 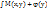 )=N(x,y) )=N(x,y)
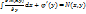 . Из последнего равенства находим . Из последнего равенства находим 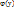 и подставляем его в (6).Восстанавливаем ф-ию u(x,y), с помощью которой описывается ур-ие (1). и подставляем его в (6).Восстанавливаем ф-ию u(x,y), с помощью которой описывается ур-ие (1).
Интегрирующий множитель .
Рассмотрим ур-ие вида (1),где ф-ияM и N и их частные производные определены в облD. Пусть для ур-ия (1) выполняется нер-во (2): 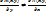 (2). (2).
Тогда ур-ие (1) не явлур-ие полных дифф-ов. Однако иногда удается подобрать такую ф-ию 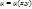 ,что преобразование ур-ие: ,что преобразование ур-ие: 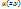 M(x,y)dx+ M(x,y)dx+ 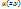 N(x,y)dy=0 (3) N(x,y)dy=0 (3)
Будет ур-ие в полных дифф-ах.Такая ф-ия  наз. интегрирующим множителем для ур-ия (1). Полагаемся найти ур-ие ,которому должны удовлетворять интегрирующий множитель наз. интегрирующим множителем для ур-ия (1). Полагаемся найти ур-ие ,которому должны удовлетворять интегрирующий множитель  .Поскаольку (3) ур-ие полных дифф-ов,то согласно критериям получаем : .Поскаольку (3) ур-ие полных дифф-ов,то согласно критериям получаем : 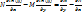 (4) (4)
Ур-ие (4), есть ур-ие с частными производными .Нахождение общего решения такого ур-ия вообще говоря задача очень сложная ,чем непосредственно интегрирования ур-ия (1).Однако, для сведенья ур-ие (1) к ур-июполныхдифф-ов (3).Достаточно найти не все ф-ии  ,а только одну,т.е. достаточно знать один интегрирующий множитель .Поэтому вместо общего решения ур-ия (4) чаще всего ищут всего одно его частное решение .С этой целью полагают ,что ф-ия ,а только одну,т.е. достаточно знать один интегрирующий множитель .Поэтому вместо общего решения ур-ия (4) чаще всего ищут всего одно его частное решение .С этой целью полагают ,что ф-ия  является ф-ий сложной от выполнения конкретной ф-ии.Чаще всего проверяют ур-ие (4)вида : является ф-ий сложной от выполнения конкретной ф-ии.Чаще всего проверяют ур-ие (4)вида : 
Например в 1-м случае ,если предположить ,что интегр. множитель зависит только от х, и не зависит от у ,то частная производная :  и ур-ие (4) принимает вид : и ур-ие (4) принимает вид : 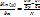 это простейшее дифф-ое ур-ие 1-го порядка .Интегрируем : это простейшее дифф-ое ур-ие 1-го порядка .Интегрируем : 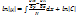 получаем получаем 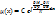 .Положим С=1,т.о интегральный множитель ур-ия (1)является ф-ей аргумента х, то он имеет вид: .Положим С=1,т.о интегральный множитель ур-ия (1)является ф-ей аргумента х, то он имеет вид: 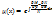 (5).Из (5) вытекает критерий,когда интегральный множитель является ф-ей аргумента х для этого необходимо ,что бы : (5).Из (5) вытекает критерий,когда интегральный множитель является ф-ей аргумента х для этого необходимо ,что бы : 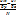 dx.Аналогично с остальными ф-ми. dx.Аналогично с остальными ф-ми.
|


 f(
f(  x,
x, 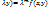 Дифф-ое ур-ие вида:M(x,y)dy+N(x,y)dx=0 (1)наз. Однородным если ф-ияM ,N однородный одной и той же степени.Однородноеур-ие (1) можно привести к ур-ию с разделяющимися переменными ,а зн может быть проинтегрирована в квадратах. В ведем в рассмотрение новую ф-июy=xu (2) и подставим в ур-ие (1) M(x,xu)d(xu)+N(x,xu)dx=0 , тогда получаемxM(1,u)du+(uM(1,u)+N(1,u)dx)=0—данное ур-ие относиться к классу с разделяющими переменными ,разделим :
Дифф-ое ур-ие вида:M(x,y)dy+N(x,y)dx=0 (1)наз. Однородным если ф-ияM ,N однородный одной и той же степени.Однородноеур-ие (1) можно привести к ур-ию с разделяющимися переменными ,а зн может быть проинтегрирована в квадратах. В ведем в рассмотрение новую ф-июy=xu (2) и подставим в ур-ие (1) M(x,xu)d(xu)+N(x,xu)dx=0 , тогда получаемxM(1,u)du+(uM(1,u)+N(1,u)dx)=0—данное ур-ие относиться к классу с разделяющими переменными ,разделим :  du+dx/x=0---ур-ие с разделенными переменными . Его общий интеграл:
du+dx/x=0---ур-ие с разделенными переменными . Его общий интеграл: 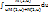 +
+ 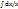 =
=  (3)
(3) - ln
- ln  +
+  )dy+N(x, x
)dy+N(x, x 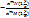 y’=-
y’=- 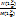 , y’(x)=f(y/x) (5) Т.о доказали ,что однородное дифф. ур-ие можно привести к виду (5).Ур-ие вида : y(x)=f(
, y’(x)=f(y/x) (5) Т.о доказали ,что однородное дифф. ур-ие можно привести к виду (5).Ур-ие вида : y(x)=f( 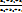 )—(6) ,для которых выражение
)—(6) ,для которых выражение 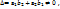 можно привести к однородному ур-ию:
можно привести к однородному ур-ию: 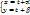 где
где  - координаты точки пересечения прямых :u=
- координаты точки пересечения прямых :u= 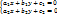 , то есть решим системы .Если
, то есть решим системы .Если  то прямые параллельны (или совпадают) ,поэтому введя в рассмотрения новую ф-ю u , по формуле: u=
то прямые параллельны (или совпадают) ,поэтому введя в рассмотрения новую ф-ю u , по формуле: u=  или u=
или u= 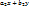 , ур-ие (6) приведем к ур-ию с разделяющимися переменными .Ур-ие (1) будет наз. обобщенным однородным ,если удается подобрать такое число
, ур-ие (6) приведем к ур-ию с разделяющимися переменными .Ур-ие (1) будет наз. обобщенным однородным ,если удается подобрать такое число  ,что левая часть ,этого ур-ия становится однородной функцией некоторой степени m относительно x,y,dx,dy при этом система х- величина измерения 1,у- величина измерения
,что левая часть ,этого ур-ия становится однородной функцией некоторой степени m относительно x,y,dx,dy при этом система х- величина измерения 1,у- величина измерения 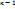 .Тогда
.Тогда 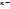 наз величиной неоднородности .Обобщенное однородное ур-ие сводится к ур-ию с разделяющимися переменными с заменой :y=u
наз величиной неоднородности .Обобщенное однородное ур-ие сводится к ур-ию с разделяющимися переменными с заменой :y=u  .
.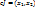 y'(x)=a(x)y—(2)-однородное ур-иет.о ,если b(x)
y'(x)=a(x)y—(2)-однородное ур-иет.о ,если b(x) 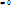 ,то (1) наз. неоднородным (1),(2) наз. соответственно. Заметим ,что (2) можно отнести к классу с разделяющимися переменными .В связи с этим можно интегрировать 2 способом ур-ие (1):1. Метод Лагранжа :
,то (1) наз. неоднородным (1),(2) наз. соответственно. Заметим ,что (2) можно отнести к классу с разделяющимися переменными .В связи с этим можно интегрировать 2 способом ур-ие (1):1. Метод Лагранжа :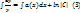 ,
, 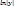 =
= 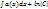 (4)
(4)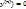 —(5).Порядок данного ур-ия можем понизить на единицу ,введя в рассмотрение функцию z=y, причем будет новой функцией z=z(y).Чтобы выполнить данную замену в ур-ие (5)необходимо выразить через саму ф-июz и ее производную :z’=dz/dy, тогда
—(5).Порядок данного ур-ия можем понизить на единицу ,введя в рассмотрение функцию z=y, причем будет новой функцией z=z(y).Чтобы выполнить данную замену в ур-ие (5)необходимо выразить через саму ф-июz и ее производную :z’=dz/dy, тогда (
( 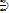 =
= 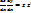
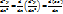 =
= 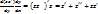 как видим из вычисленной производной ф-ииу к-го порядка выражается через производные ф-ииz порядков к-1 и ниже, что приводит при подставке и в ур-ие (5) понижение порядка на единицу .В частности если ур-ие (5) ур-ие 2-го порядка ,то указанная замена приводит его к ур-ию 1-го порядка т.о. с помощью указанной заменой ,ур-ие (5) приводится к виду:
как видим из вычисленной производной ф-ииу к-го порядка выражается через производные ф-ииz порядков к-1 и ниже, что приводит при подставке и в ур-ие (5) понижение порядка на единицу .В частности если ур-ие (5) ур-ие 2-го порядка ,то указанная замена приводит его к ур-ию 1-го порядка т.о. с помощью указанной заменой ,ур-ие (5) приводится к виду:  =(y,z,
=(y,z, 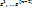 ) его общее решение зависит от z=z(y,
) его общее решение зависит от z=z(y, 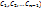 . Учитывая замену ,получим ур-ие с разделяющимися переменными ,метод интегрирования который рассматривали ранние.
. Учитывая замену ,получим ур-ие с разделяющимися переменными ,метод интегрирования который рассматривали ранние.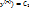 --(7)представляет собой дифф-оеур-ие порядка (n-1),т.е. понизили порядок ур-ия (6)на единицу. Такое выражение (7)наз. 1-ым интегралом ур-ия (6).
--(7)представляет собой дифф-оеур-ие порядка (n-1),т.е. понизили порядок ур-ия (6)на единицу. Такое выражение (7)наз. 1-ым интегралом ур-ия (6). —(4’)
—(4’)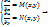 (5’) ,
(5’) , 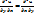 ,
, 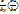 =
= 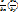
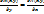 --(4)
--(4) dx+
dx+  dy= M(x,y)dx+N(x,y)dy ,
dy= M(x,y)dx+N(x,y)dy , 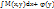 --(6) ,
--(6) ,  (
( 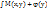 )=N(x,y)
)=N(x,y)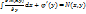 . Из последнего равенства находим
. Из последнего равенства находим 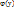 и подставляем его в (6).Восстанавливаем ф-ию u(x,y), с помощью которой описывается ур-ие (1).
и подставляем его в (6).Восстанавливаем ф-ию u(x,y), с помощью которой описывается ур-ие (1).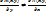 (2).
(2).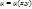 ,что преобразование ур-ие:
,что преобразование ур-ие: 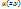 M(x,y)dx+
M(x,y)dx+  наз. интегрирующим множителем для ур-ия (1). Полагаемся найти ур-ие ,которому должны удовлетворять интегрирующий множитель
наз. интегрирующим множителем для ур-ия (1). Полагаемся найти ур-ие ,которому должны удовлетворять интегрирующий множитель 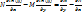 (4)
(4)
 и ур-ие (4) принимает вид :
и ур-ие (4) принимает вид : 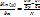 это простейшее дифф-ое ур-ие 1-го порядка .Интегрируем :
это простейшее дифф-ое ур-ие 1-го порядка .Интегрируем : 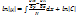 получаем
получаем 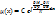 .Положим С=1,т.о интегральный множитель ур-ия (1)является ф-ей аргумента х, то он имеет вид:
.Положим С=1,т.о интегральный множитель ур-ия (1)является ф-ей аргумента х, то он имеет вид: 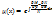 (5).Из (5) вытекает критерий,когда интегральный множитель является ф-ей аргумента х для этого необходимо ,что бы :
(5).Из (5) вытекает критерий,когда интегральный множитель является ф-ей аргумента х для этого необходимо ,что бы : 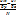 dx.Аналогично с остальными ф-ми.
dx.Аналогично с остальными ф-ми.