
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные правила дифференцирования.Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х. 1) (u ± v)¢ = u¢± v¢ 2) (u×v)¢ = u×v¢ + u¢×v 3) Эти правила могут быть легко доказаны на основе теорем о пределах. Производные основных элементарных функций. 1)С¢ = 0; 9) 2)(xm)¢ = mxm-1; 10) 3) 11) 4) 12) 5) 13) 6) 14) 7) 15) 8) 16)
Логарифмическое дифференцирование. Рассмотрим функцию Тогда (lnïxï)¢=
Учитывая полученный результат, можно записать Отношение Способ логарифмического дифференцированиясостоит в том, что сначала находят логарифмическую производную функции, а затем производную самой функции по формуле
Способ логарифмического дифференцирования удобно применять для нахождения производных сложных, особенно показательных функций, для которых непосредственное вычисление производной с использованием правил дифференцирования представляется трудоемким.
Производные и дифференциалы высших порядков. Производная параметрически заданных функций. Производные и дифференциалы высших порядков. Пусть функция f(x)- дифференцируема на некотором интервале. Тогда, дифференцируя ее, получаем первую производную
Если найти производную функции f¢(x), получим вторую производнуюфункции f(x).
т.е. y¢¢ = (y¢)¢ или
Этот процесс можно продолжить и далее, находя производные степени n.
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 225. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , если v¹ 0
, если v¹ 0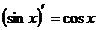
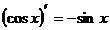



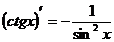






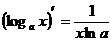

 .
. , т.к.
, т.к.  .
.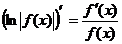 .
. называется логарифмической производной функции f(x).
называется логарифмической производной функции f(x).



 .
. .
.