
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные правила дифференцирования.1) Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:
2) Производная произведения двух дифференцируемых функций равна сумме произведений производной первого сомножителя на второй и производной второго сомножителя на первый:
3) Производная частного двух дифференцируемых функций может быть найдена по формуле:
4) Постоянный множитель можно выносить за знак производной:
Таблица производных.
Пример 8.2. Найти производную функции Решение: Используя правила дифференцирования (1 и 4) и таблицу производных, находим, что
Пример 8.3. Найти производную функции Решение: Используя правило дифференцирования (2) и таблицу производных, находим, что
Пример 8.4. Найти производную функции Решение: Используя правило дифференцирования (3) и таблицу производных, находим, что
Производная сложной функции. Пусть Теорема 8.1.Если
Пример 8.5. Найти производную функции Решение: Исходную функцию можно представить в виде  1) 2) 3) Следовательно, Логарифмическое дифференцирование. Определение 8.4.Логарифмическое дифференцирование – это метод отыскания производной заданной функции путем предварительного ее логарифмирования. Замечание 8.1.Этот метод широко используется для нахождения производной от фукции вида
Дифференцируя последнее соотношение, имеем
Умножая обе части этого равенства на
Пример 8.6. Найти производную функции Решение: Применим метод логарифмического дифференцирования:
Производная неявной функции. Определение 8.5.Если
где Для нахождения производной функции Пример 8.7. Найти производную функции Решение: Дифференцируем обе части равенства, рассматривая
Решаем полученное уравнение относительно
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 235. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
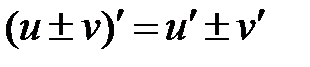 .
.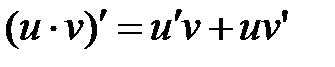 .
.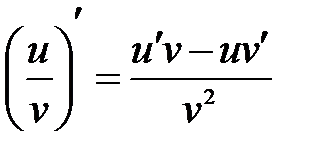 .
.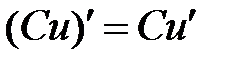 .
.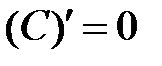 .
.
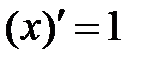 .
.
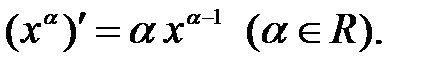
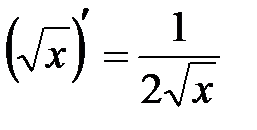 .
.
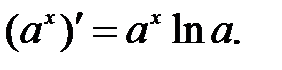
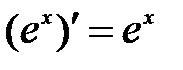
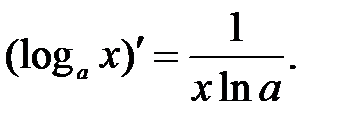
 .
.
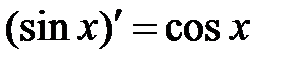 .
.
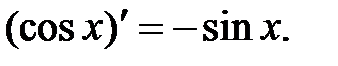
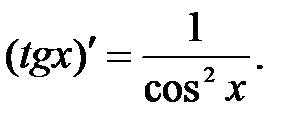
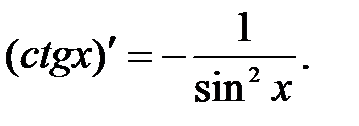
 .
.
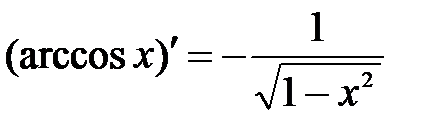 .
.
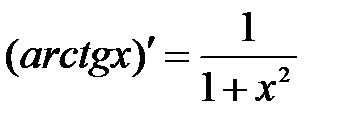 .
.
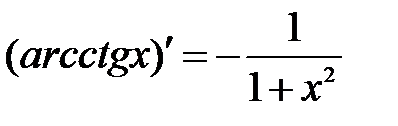 .
.
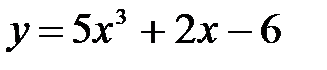 .
.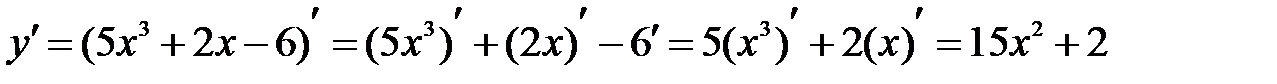 .
. .
.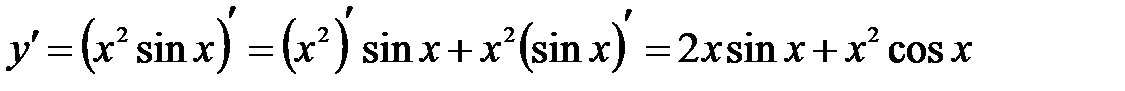 .
.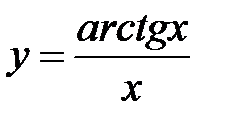 .
.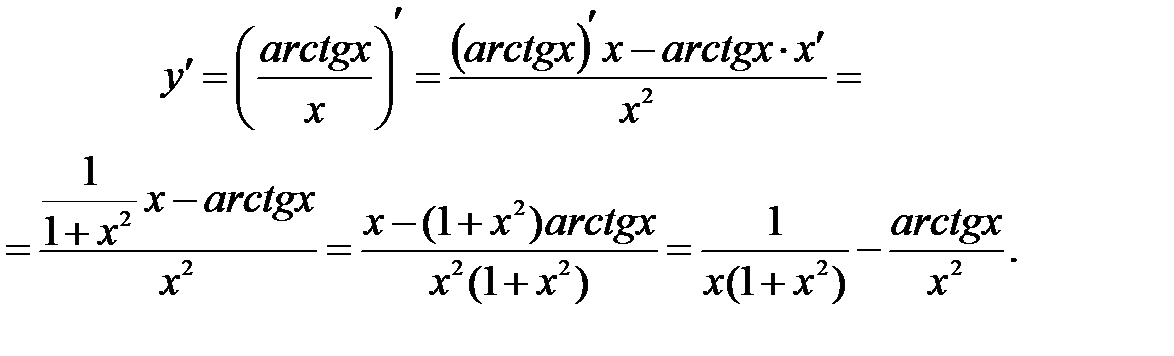
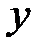 есть функция от переменной
есть функция от переменной 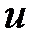 (
( 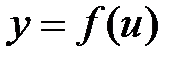 ), а переменная
), а переменная 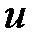 в свою очередь есть функция от независимой переменной
в свою очередь есть функция от независимой переменной 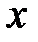 (
( 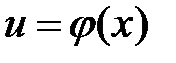 ), т.е. задана сложная функция
), т.е. задана сложная функция 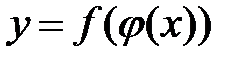 . Функция
. Функция 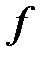 является внешней функцией, а функция
является внешней функцией, а функция 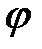 – внутренней.
– внутренней.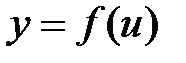 и
и 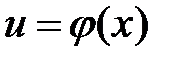 – дифференцируемые функции от своих аргументов, то производная сложной функции
– дифференцируемые функции от своих аргументов, то производная сложной функции 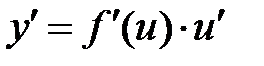 .
.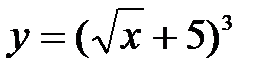 .
.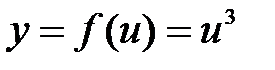 , где
, где 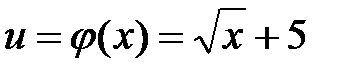 . Тогда, согласно теореме 8.1 о производной сложной функции, будем иметь:
. Тогда, согласно теореме 8.1 о производной сложной функции, будем иметь: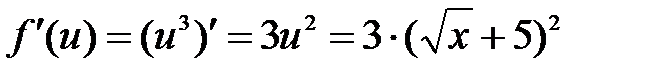 ;
; ;
;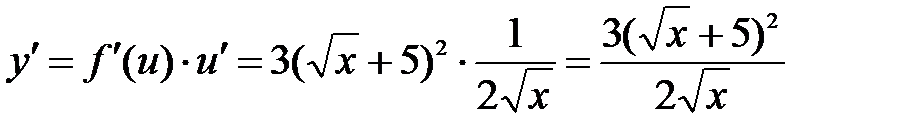 .
.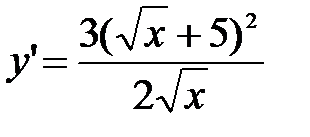 .
.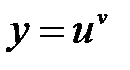 , где
, где 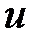 и
и 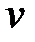 – функции аргумента
– функции аргумента 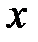 . Действительно, логарифмируя обе части исходного равенства, получаем
. Действительно, логарифмируя обе части исходного равенства, получаем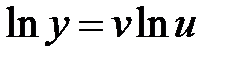 .
.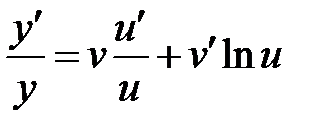 .
. и заменяя затем
и заменяя затем 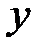 через
через 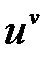 , после простых преобразований окончательно получаем, что
, после простых преобразований окончательно получаем, что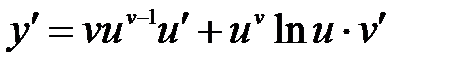 .
.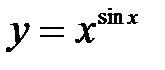 .
.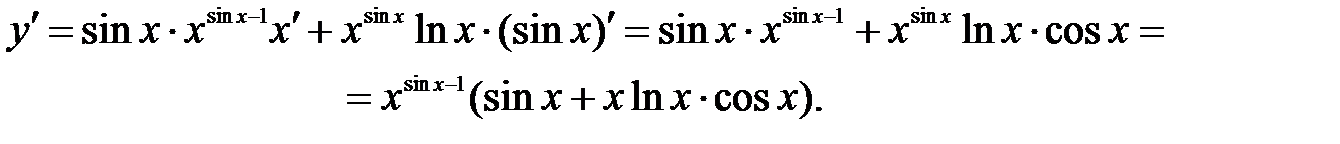
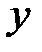 как функция от
как функция от 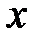 задается посредством соотношения
задается посредством соотношения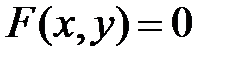 ,
,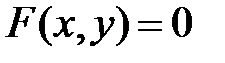 – выражение, содержащее
– выражение, содержащее 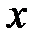 и
и 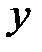 , то
, то 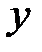 называется неявной функциейот
называется неявной функциейот 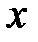 .
.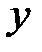 , заданной неявно, нужно продифференцировать обе части уравнения, рассматривая
, заданной неявно, нужно продифференцировать обе части уравнения, рассматривая  как функцию от
как функцию от 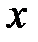 , а затем из полученного уравнения найти производную
, а затем из полученного уравнения найти производную 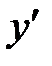 .
.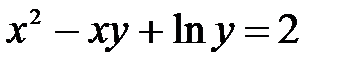 .
.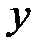 как функцию от
как функцию от 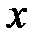 :
: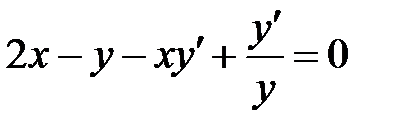 .
.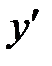 :
: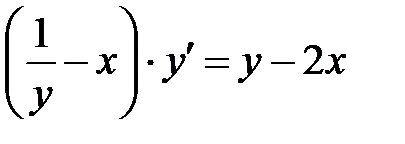 ;
; 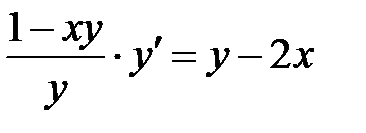 ;
; 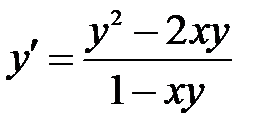 .
.