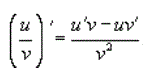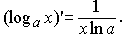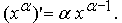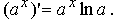Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Определение непрерывности функции Пусть функция f(x) определена на некотором интервале(a b) , для которого x0 -- внутренняя точка. Функция называется непрерывной в точке x0, если существует предел при и этот предел равен значению f(x) , то есть
Пусть функция определена на некотором полуинтервале , для которого -- левый конец. Функция называется непрерывной справа в точке , если существует предел при и этот предел равен значению , то есть
Билет 18. Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс — интегрирование. Производные суммы, разности, произведения, частного Производная суммы (разности) функций Производная алгебраической суммы функций выражается следующей теоремой. Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:
Производная конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых. Например, Производная произведения функций. Пусть u(x) и u(x) - дифференцируемые функции. Тогда произведение функций u(x)v(x) также дифференцируемо и Производная частного функций.  Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0, то производная частного этих функций вычисляется по формуле Производные основных элементарных функций Теорема 6. (производная логарифмической функции)
Теорема 7. (производная степенной функции) Теорема 8. (производная показательной функции) Теорема 9. (производные тригонометрических функций)
Теорема 10. (производные обратных тригонометрических функций)
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 275. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
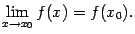
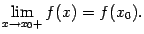
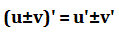
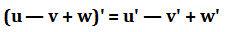
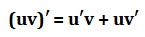 Производная произведения двух функций не равана произведению производных этих функций.
Производная произведения двух функций не равана произведению производных этих функций.