
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Острый угол между прямой и плоскостьюСтр 1 из 2Следующая ⇒ Лекция №11. Прямая в пространстве. Прямая и плоскость. Уравнения прямой в пространстве Общее уравнение прямой Прямая в пространстве рассматривается как линия пересечения двух плоскостей. Общее уравнение прямой в пространстве: Канонические уравнения прямой Определение: Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором Канонические уравнения прямой, проходящей через точку
Рис. 1 Если
Параметрические уравнения прямой Параметрические уравнения прямой: Замечание 1. В уравнениях t рассматривается как произвольно изменяющийся параметр; x, y, z – как функции от t. Замечание 2. Параметрические уравнения прямой удобно применять в тех случаях, когда требуется найти точку пересечения прямой с плоскостью. Уравнение прямой, проходящей через две данные точки Уравнение прямой, проходящей через две данные точки
Через две точки можно провести единственную прямую. Прямая линия в пространстве. Основные задачи Угол между прямыми Углом между прямыми в пространстве будем называть любой из углов, образованных двумя прямыми, проведенными через произвольную точку параллельно данным прямым. Угол между прямыми
Для нахождения острого угла между прямыми числитель правой части формулы следует взять по модулю. Замечание 1. За угол  Замечание 2. В формуле можно ставить любой знак, что соответствует выбору одного из двух различных углов между данными прямыми. Условие параллельности двух прямых. Условие параллельности двух прямых: Это условие можно получить, заметив, что векторы Условие перпендикулярности двух прямых. Условие перпендикулярности двух прямых: Прямые перпендикулярны, если скалярное произведение направляющих векторов Условие при котором две прямые лежат в одной плоскости Пусть прямые
Прямая
При выполнении этого условия прямые
Задачи
Задача 1. Общие уравнения прямой Решение Первый способ Наметим такой план решения задачи: из системы исключим сначала y и выразим z через x, потом исключим x и выразим z теперь уже через y. Для того, чтобы из системы исключить y, сложим первое уравнение системы почленно со вторым. Получим, что Умножая первое уравнение системы (9) на 2, а второе на (-3) и складывая их почленно, получим откуда или Сравнивая найденные значения z, получаем уравнения прямой в каноническом виде: Умножая теперь все знаменатели на 15, окончательно получим Второй способ Найдем направляющий вектор Таким образом,
Итак, искомые канонические уравнения прямой имеют вид Замечание. В общем случае точка Задача 2. Составить уравнение прямой, проведенной через точку Решение Способ первый Запишем уравнения любой прямой, проходящей через точку M: Из условия ее перпендикулярности к данным прямым, имеем Откуда Подставляя найденные значения в (*) получим: Способ второй
Следовательно, направляющим вектором искомой прямой может быть вектор Таким образом, имеем Прямая и плоскость Острый угол между прямой и плоскостью Углом
Рис. 2 Острый угол между прямой
Замечание. Угол Так как |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 218. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
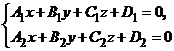 .
. этой прямой.
этой прямой. и параллельной вектору
и параллельной вектору 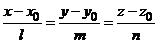
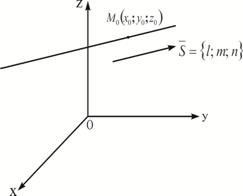
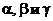 - углы между прямой и координатными осями
- углы между прямой и координатными осями  ,
, 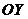 и
и 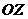 ,
, 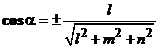 ;
;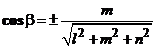 ;
;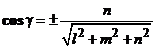 ,
,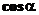 ,
, 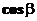 ,
, 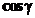 - называются направляющими косинусами прямой.
- называются направляющими косинусами прямой.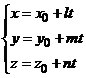 .
.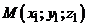 и
и 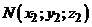 :
: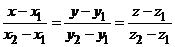 .
.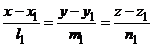 ,
, 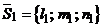 и
и 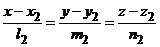 ,
,  определяется по формуле:
определяется по формуле: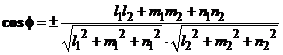 .
.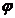 между прямыми можно принять угол между их направляющими векторами
между прямыми можно принять угол между их направляющими векторами 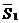 и
и 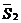 .
.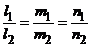 .
.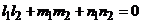 .
.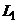 и
и 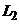 заданы каноническими уравнениями
заданы каноническими уравнениями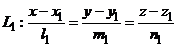 ,
, 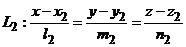 ,
, 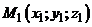 , прямая
, прямая 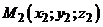 . Тогда
. Тогда 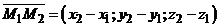 . Прямые
. Прямые 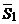 ,
,  и
и  компланарны. Условием компланарности векторов является равенство нулю их смешанного произведения:
компланарны. Условием компланарности векторов является равенство нулю их смешанного произведения: 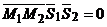 , т. е.
, т. е.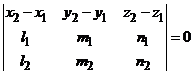 .
.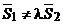 , либо параллельны
, либо параллельны 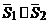 .
. преобразовать к каноническому виду.
преобразовать к каноническому виду.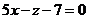 , откуда
, откуда 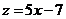 ,
, 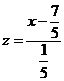 .
.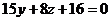 ,
,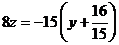
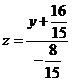 .
.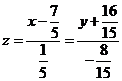 или
или 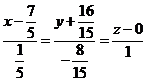 .
.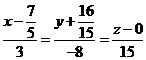 . Прямая проходит через точку
. Прямая проходит через точку  и имеет направляющий вектор
и имеет направляющий вектор 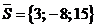 .
.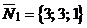 и
и 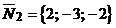 , то в качестве его можно взять векторное произведение векторов
, то в качестве его можно взять векторное произведение векторов 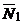 и
и 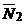 :
: 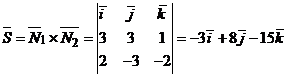 .
.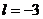 ,
, 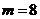 ,
, 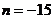 . За точку
. За точку 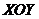 . Поскольку при этом
. Поскольку при этом 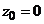 , координаты
, координаты 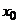 и
и 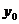 определяются из системы уравнений заданных плоскостей, если положить в них
определяются из системы уравнений заданных плоскостей, если положить в них 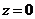 .
. отсюда получаем
отсюда получаем 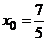 ,
, 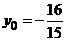 .
.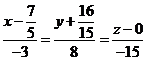 или
или 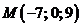 перпендикулярно двум данным прямым:
перпендикулярно двум данным прямым: 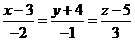 ,
, 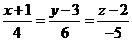 .
.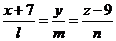 (*).
(*).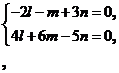
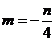 ;
; 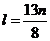 .
.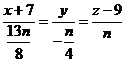 или
или 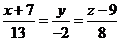 .
.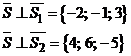 .
.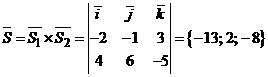 или
или 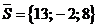 .
.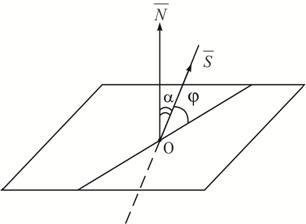
 и плоскостью
и плоскостью 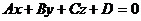 определяется по формуле:
определяется по формуле: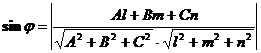
 находим из скалярного произведения нормального вектора
находим из скалярного произведения нормального вектора 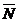 плоскости и направляющего вектора
плоскости и направляющего вектора  прямой.
прямой.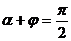 , то
, то 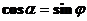 .
.