
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные элементарные функции
1) степенная: 2) логарифмическая: 3) показательная: 4) тригонометрические: 5) обратные тригонометрические: Показательная и линейная функции находят применение в финансовых вычислениях. Большинство банковских операций состоит в выдаче денег «в рост» и «под процент». Наращенный (конечный) капитал
где По первой формуле начисляют простые проценты, по второй – сложные. В первой формуле используется линейная зависимость, во второй формуле – показательная. Пример.Сбербанк начисляет ежемесячно по сложной процентной ставке
Пределы Понятие предела – очень сложное понятие современной математики. Это хорошо иллюстрируется исторической картиной его внедрения. Само понятие появилось в середине XVII века в работах великих математиков Ньютона и Лейбница, однако строгая теория пределов была создана лишь 200 лет спустя – в XIX веке – в трудах французского математика Коши. Рассмотрим примеры вычисления пределов простейших функций: числовых последовательностей. Числовой последовательностью называется функция от натурального аргумента, то есть функция, заданная на множестве натуральных чисел Последовательность  Аналогично, Определение 2. Число Числовая последовательность Величина, обратная бесконечно малой, называется бесконечно большой. Например, Последовательность, имеющая конечный предел, называется сходящейся, а не имеющая конечного предела – расходящейся. Предел функции от действительной переменной обозначается аналогично пределу числовой последовательности: Определение 3.Число
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 182. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
,  .
. ,
,  .
. ,
, 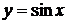 ,
,  ,
,  ,
,  .
. ,
, 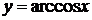 ,
,  ,
,  .
.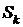 вычисляется по формулам:
вычисляется по формулам: ,
, – начальный капитал,
– начальный капитал, 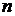 – период начисления процентов,
– период начисления процентов, 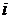 – процентная ставка.
– процентная ставка. годовых. Определить сумму вклада после 8 месяцев хранения, если первоначальный вклад составил 360 руб.
годовых. Определить сумму вклада после 8 месяцев хранения, если первоначальный вклад составил 360 руб.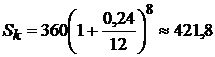 .
.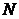 . Числовые последовательности принято обозначать следующим образом:
. Числовые последовательности принято обозначать следующим образом:  . Например,
. Например,  ,
,  ,
,  – числовые последовательности.
– числовые последовательности. Если изобразить эти точки на числовой прямой, то видно, что числовая последовательность движется к нулю. Говорят, что её предел равен нулю и записывают
Если изобразить эти точки на числовой прямой, то видно, что числовая последовательность движется к нулю. Говорят, что её предел равен нулю и записывают  .
.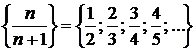 и
и  ;
; 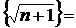
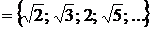 и
и  .
.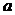 называется пределом последовательности
называется пределом последовательности  существует номер
существует номер  такой, что при любых
такой, что при любых 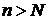 выполняется неравенство
выполняется неравенство  . Это обозначается следующим образом:
. Это обозначается следующим образом:  .
. называется бесконечно малой, если её предел равен нулю. Например, последовательность
называется бесконечно малой, если её предел равен нулю. Например, последовательность  – бесконечно большая числовая последовательность. Предел бесконечно большой последовательности обозначается
– бесконечно большая числовая последовательность. Предел бесконечно большой последовательности обозначается  или
или  .
. .
. называется пределом функции
называется пределом функции  при
при  , стремящемся к
, стремящемся к  , если для любого положительного числа
, если для любого положительного числа  можно указать интервал, содержащий точку
можно указать интервал, содержащий точку  , такой, что всюду внутри этого интервала, за исключением, быть может, самой точки
, такой, что всюду внутри этого интервала, за исключением, быть может, самой точки 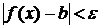 .
.