
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Показательная форма комплексного числа. Формула Эйлера.Рассмотрим степень Если х = 0, то получим соотношение, которое называется формулой Эйлера Показательная функция имеет период, равный 2πi, т. е. Тригонометрическую форму комплексного числа z = r( Эта запись называется показательной или экспоненциальной формой комплексного числа. Для комплексных показателей справедливы основные правила действий с показателями: 1) Правило: При умножении чисел показатели складываются. r1 2) Правило:При делении чисел показатели вычитаются. 3) Правило:При возведении в степень показатели перемножаются. (r Формула Эйлера (12) устанавливает связь между тригонометрическими функциями и показательной функцией. Заменим в этой формуле у на φ и на – φ, получим
Складывая и вычитая эти равенства, получим:  Формулы (18) и (19), также называются формулами Эйлера.Они выражают тригонометрические функции через показательные. Пример 11:Представьте в показательной форме комплексное число z = - 2 + 2 Решение: Используя формулу (5), находим r =
Ответ: z = 4
У п р а ж н е н и я д л я с а м о п р о в е р к и: 1. Найдите модуль и главное значение аргумента комплексных чисел: а) z = 1 + i; б) z = 2 - 2i. 2. Решите квадратные уравнения: а) х2 + х + 1 = 0; б) х2 + 1 = 0 3. Даны два числа z1 = 2 + 3i; z2 = 1 – 2i. Найдите сумму и разность этих чисел. 4. Найдите х и у из уравнения: (1 + 2i)x + (3 – 5i)y = 1 – 3i. 5. Дано z1 = 6. Представьте в экспоненциальной форме комплексное число 2 + 2i. 7. Дано z1 = 2e – I; z2 = 0.5e0.5i. Найдите: z1z2 Ответы:1.а) r =
Пределы. Определение1:Число А называется пределом функции f(х) при х →а, если для любого число ε > 0 можно указать δ >0, что для любого х ≠ а, удовлетворяющему неравенству 0<|х – а |<δ, выполняется неравенство |f(х) – А |<ε. В этом случае пишут Определение 2:Функция f(х) называется бесконечно малой при х →а, если Пример1: Определение 3: Функция f(х) называется бесконечно большой при х →а, если Пример2: Свойства бесконечно малой и бесконечно большой функций: 1.Если f(х) – бесконечно малая функция, то 2.Если f(х) – бесконечно большая функция, то Теоремы о пределах. Теорема 1:Если существуют пределы функций f(х) и g(х), то существует и предел их суммы, равный сумме пределов функций f(х) и g(х): Теорема 2:Если существуют пределы функций f(х) и g(х), то существует и предел их произведения, равный произведению пределов функций f(х) и g(х): Теорема № 3:Если существуют пределы функций f(х) и g(х), предел функции g(х) отличный от 0, то существует и предел их отношения, равный отношению пределов функций f(х) и g(х): Следствия. Следствие 1:Постоянный множитель можно выносить за знак предела. Следствие 2:Предел степени равен степени пределов. Следствие 3: |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 256. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 с комплексным показателем z = χ + iy, где e = 2,7182… – основание натурального логарифма, то
с комплексным показателем z = χ + iy, где e = 2,7182… – основание натурального логарифма, то 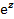 =
=  , т.е.
, т.е. =
=  (11)
(11) =
=  (12)
(12) . При z = 0 получим соотношение
. При z = 0 получим соотношение  .
.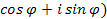 можно записать виде: z = r
можно записать виде: z = r  ,
, 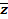 = r
= r  (13)
(13) (14)
(14)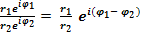 (15)
(15) 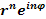 (16)
(16)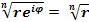 *
*  (k = 0,1,2,…,n – 1) (17)
(k = 0,1,2,…,n – 1) (17) =
= 
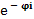 =
= 
 (18)
(18) (19)
(19) i.
i. = 4. По формуле (13) найдём
= 4. По формуле (13) найдём ;
;  =
= 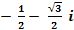 . По формуле (18) и (19) вычислим значение
. По формуле (18) и (19) вычислим значение  = -
= -  и
и  =
=  , т.о. φ = -
, т.о. φ = - 
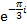
 z2 =
z2 = 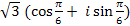 Найдите z1z2
Найдите z1z2 ; φ =
; φ =  . б) r =
. б) r = 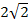 ; φ = -
; φ = -  ; б)
; б) 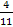 ; y =
; y =  . 5.
. 5. 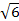 (
( 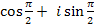 ). 6. 2
). 6. 2  . 7. e- 0.5i.
. 7. e- 0.5i. = А.
= А. 
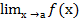 = 0
= 0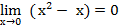
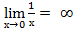 .
.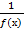 - бесконечно большая функция.
- бесконечно большая функция. (f(х) + g(х))=
(f(х) + g(х))=  +
+  g(x).
g(x).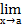 f(x)*.
f(x)*. 
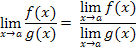
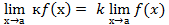
 = (
= (  )n.
)n. = с.
= с.