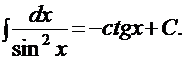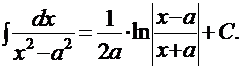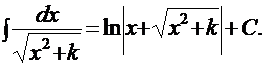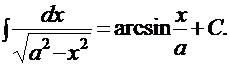Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Первообразная и неопределенный интегралВ предыдущей теме 4 пособия введены понятия производной и дифференцирования функции. Обратной операцией для дифференцирования функции является операция интегрирования функции, или операция нахождения ее первообразной.
Определение.Функция F (x) называется первообразной для функции f (x) на некотором промежутке Х, если для всех х этого промежутка выполняется равенство: F′(x) = f (x).
ПРИМЕРЫ: 1. Функция F(x) = sin x будет являться первообразной для функции f (x) = cos x, поскольку для любых действительных х справедливо равенство: (sin x)′ = cos x. 2. Функция F(x) = x3 будет являться первообразной для функции f (x) = 3x2, поскольку для любых действительных х справедливо равенство: (х3)′ = 3х2. Задача отыскания по данной функции ее первообразной решается неоднозначно. Действительно, если F(x) является первообразной для функции f (x), т.е. F′(x) = f (x), то функция Φ(x) = F(x) + C, где С – произвольная постоянная, также будет первообразной для функции f (x), поскольку: Φ′(х) = F′(x) + 0 = f (x). Отсюда следует, что множество всех первообразных для некоторой данной функции состоит из функций, отличающихся друг от друга на постоянную величину, которая, в свою очередь, может принимать произвольные действительные значения.
Определение.Если функция F(x) является первообразной для функции f (x), то множество функций F(x) + C, где С – произвольная постоянная, называется неопределенным интегралом от функции f (x) и обозначается символом:
При этом функция f (x) называется подынтегральной функцией, выражение f (x)dx – подынтегральным выражением, dx – дифференциалом переменной х, которая в этом случае называется переменной интегрирования. 
Основные свойства неопределенного интеграла Из определения неопределенного интеграла непосредственно вытекают следующие его основные свойства.
1). Производная неопределенного интеграла равна подынтегральной функции, а дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.:
2). Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.:
3). Постоянный множитель можно выносить за знак неопределенного интеграла, т.е. если k = const ¹ 0, то:
4). Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме неопределенных интегралов от этих функций, т.е.:
Таблица основных неопределенных интегралов
В приведенной ниже таблице основных неопределенных интегралов часть формул (1÷10) следует из определения интегрирования как операции, обратной дифференцированию, и из таблицы производных простейших элементарных функций. Справедливость остальных формул легко может быть проверена дифференцированием.
1). 3). 5). 7). 9). 11). 12). 13). 14). Неопределенные интегралы, содержащиеся в этой таблице, условно называются табличными. Основные методы интегрирования |
|||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 234. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
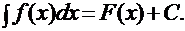
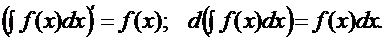
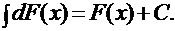
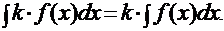
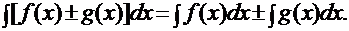
 2).
2). 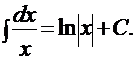
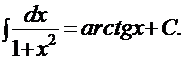 4).
4). 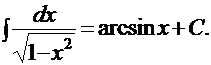
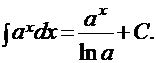 6).
6). 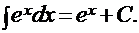
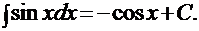 8).
8). 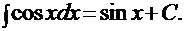
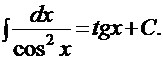 10).
10).