
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Множества и операции над нимиСтр 1 из 20Следующая ⇒ ДИСКРЕТНАЯ МАТЕМАТИКА
Кемерово 2011 Составители: доцент С. Г. Гутова, старший преподаватель Т. А. Невзорова .
Дискретная математика: учеб.-метод. пособие/ ФГБОУ ВПО «Кемеровский государственный университет»; сост. С. Г. Гутова, Т. А. Невзорова. – Кемерово, 2011. – 128 с.
Учебно-методическое пособие разработано по дисциплине «Дискретная математика» для направлений 010300 – «Фундаментальная информатика и информационные технологии» и 010400 – «Прикладная математика и информатика» в соответствии с требованиями ГОС ВПО и включает краткий теоретический материал, примеры решения задач, упражнения для аудиторной и самостоятельной работы, методические рекомендации. Предназначено для студентов 1 курса математического факультета.
Оглавление ГЛАВА 1. ТЕОРИЯ МНОЖЕСТВ. 4 ДИСКРЕТНАЯ ТЕОРИЯ ВЕРОЯТНОСТИ.. 4 1.1. Множества и операции над ними.. 4 1.2. Векторы и прямые произведения множеств. 8 Проекция вектора на ось. 8 1.4. Введение в дискретную теорию вероятностей.. 17 1.5. Соответствия и функции.. 25 1.6. Отношения. 31 1.7. Операции и алгебры.. 38 1.8. Гомоморфизм и изоморфизм алгебр.. 41 ГЛАВА 2. ТЕОРИЯ ГРАФОВ.. 49 2.1. Основные определения, способы задания, 49 основные классы, изоморфизм графов. 49 2.2. Маршруты, цепи и циклы. Расстояния, диаметры, центры. Обходы. Разделяющие множества и разрезы 59  2.3 Деревья, их свойства. 66 Характеристические числа графов. Сети.. 66 ГЛАВА 3. ДИСКРЕТНЫЕ СТРУКТУРЫ: КОНЕЧНЫЕ АВТОМАТЫ, КОДЫ... 72 3.1. Машина Тьюринга. 73 3.2. Основы теории кодирования. 77 ГЛАВА 4. АЛГЕБРА ЛОГИЧЕСКИХ ФУНКЦИЙ.. 85 4.1. Основные определения. 85 4.3. Дизъюнктивные и конъюнктивные нормальные формы.. 90 4.4. Дизъюнктивные нормальные формы и импликанты.. 92 4.5. Минимизация ДНФ. Тупикова ДНФ.. 95 4.6. Алгебра Жегалкина. 100 4.7. Двойственность. 101 4.8. Функциональная полнота систем.. 104 ГЛАВА 5. ЛОГИКА ВЫСКАЗЫВАНИЙ.. 106 И ЛОГИКА ПРЕДИКАТОВ.. 106 5.1. Логика высказываний.. 106 5.2. Логика предикатов. 114 ГЛАВА 6. СХЕМЫ ПЕРЕКЛЮЧАТЕЛЕЙ. 120 КОМБИНАЦИОННЫЕ СХЕМЫ... 120 6.1. Схемы переключателей.. 120 6.2. Комбинационные схемы.. 122 Литература. 127
ГЛАВА 1. ТЕОРИЯ МНОЖЕСТВ. ДИСКРЕТНАЯ ТЕОРИЯ ВЕРОЯТНОСТИ Множества и операции над ними Множество можно представить как совокупность некоторых объектов, объединенных по какому-либо признаку. Множество состоит из элементов. В зависимости от их числа множества различают как конечные или бесконечные. Конечные множества могут состоять из одного или нескольких элементов. Мощность множества – количество его элементов. Множество, не содержащее элементов, называется пустым множеством и обозначается Æ. Множество обозначают заглавными буквами, а его элементы – прописными. Для записи множества используют фигурные скобки. Например, множество натуральных чисел от 3 до 10: М = {3, 4, 5, 6, 7, 8, 9, 10}. Говоря об определенном множестве, мы полагаем, что для каждого объекта имеется две возможности: либо он входит в рассматриваемое множество, т.е. является его элементом, принадлежит ему (обозначается Способы задания множества: - перечисление всех элементов множества, например, множество однозначных неотрицательных чисел X = {0, 1, 2, 3, …, 9}; - указание общего свойства, которым обладают все элементы множества, например, множество четных натуральных чисел X = {2, 4, 6, 8, 10, 12, …} или X = {x: x = 2n, - рекуррентно, например: Множество А называют подмножеством множества В (обозначается Множества А и В называют равными ( Множество I называется универсальным множеством (множество всех подмножеств) для некоторой системы множеств, если каждое множество этой системы является подмножеством I, т.е. {A, B, C, …}: Дополнением множества А ( Объединением двух множеств А и В ( Пересечением двух множеств А и В ( Разностью двух множеств А и В (
Прямым (декартовым) произведением двух множеств А и В ( Пример. Заданы два множества: А = {-2, -1, 0, 1, 2} и B = {0, 2, 4, 5}. Определить множества Множество А = {-2, -1, 0, 1, 2} состоит из пяти элементов, следовательно мощность этого множества равна 5: Аналогично, B = {0, 2, 4, 5} содержит четыре элемента: По определению пересечение двух множеств состоит только из общих для обоих множеств элементов, следовательно, По определению объединение двух множеств состоит из всех элементов, которые принадлежат и множеству А, и множеству В, следовательно, Множество Аналогично, Прямое (декартово) произведение:
Из этого примера видно, что УПРАЖНЕНИЯ 1. Укажите смысловые связки естественного языка, соответствующие основным операциям над множествами: дополнение (– НЕ), объединение (сумма) (– ИЛИ), пересечение (произведение) (– И), разность (– БЕЗ). 2. Пусть
3. Заданы множества А = {1, 5, 7, 9, 12} , B = {5, 7, 9, 11, 13} и С = {1, 2, 3, 8, 10}, являющиеся подмножеством универсального множества U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}. Найти следующие множества и их мощности:
4. По заданным промежуткам А и B на числовой оси определить 1) 2) 5. Задана система множеств 6. Задана система множеств Найти 7. Пусть А и В – произвольные подмножества универсального множества I. Доказать графически, что: 1) 2) 3) 8. Доказать (аналитически), что Указание: воспользоваться тождеством 9. Существуют ли такие множества А, В и С, что Указание: построить диаграмму Эйлера – Венна. 11. Построить из множества А, В и С результат операций над ними. 1) 12. Пусть Множества А, В, С пересекаются в наиболее общем случае. Изобразить на диаграмме Эйлера Результат следующих действий: 1) 13. Пусть 14. Пусть А, В и С – множества такие, что 15. Указать, какие из следующих равенств верны для любых множеств; верны для некоторых множеств; неверны или бессмысленны. Привести обоснование.
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 360. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
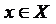 ); либо нет (обозначается
); либо нет (обозначается 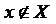 ).
).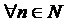 };
};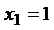 ,
, 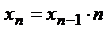 и др.
и др.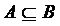 ), если каждый элемент множества А является также элементом множества В.
), если каждый элемент множества А является также элементом множества В.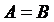 ), если каждый элемент множества А является одновременно элементом множества В и наоборот, т.е. если
), если каждый элемент множества А является одновременно элементом множества В и наоборот, т.е. если 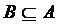 . Другими словами, два множества равны, если они состоят из одних и тех же элементов.
. Другими словами, два множества равны, если они состоят из одних и тех же элементов.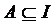 ,
, 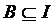 ,
, 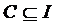 , …
, …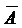 ) называется множество, состоящее из тех и только тех элементов универсального множества, которые не входят в множество А.
) называется множество, состоящее из тех и только тех элементов универсального множества, которые не входят в множество А.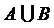 ) называется множество С, состоящее из тех элементов, которые принадлежат или множеству А, или В, или А и В одновременно.
) называется множество С, состоящее из тех элементов, которые принадлежат или множеству А, или В, или А и В одновременно.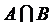 ) называется множество С, состоящее из тех и только тех элементов, которые принадлежат множествам А и В одновременно.
) называется множество С, состоящее из тех и только тех элементов, которые принадлежат множествам А и В одновременно.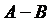 или
или 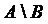 ) называется множество тех элементов множества А , которые не принадлежат множеству В:
) называется множество тех элементов множества А , которые не принадлежат множеству В: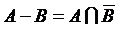 .
.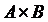 ) называется множество, состоящее из упорядоченных пар элементов, в которых первый элемент принадлежит множеству А, а второй – множеству В.
) называется множество, состоящее из упорядоченных пар элементов, в которых первый элемент принадлежит множеству А, а второй – множеству В.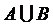 ;
; 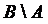 ;
; 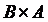 и их мощность.
и их мощность.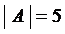 .
.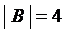 .
.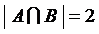 .
.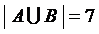 .
.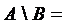
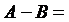 {-2, -1, 1} и
{-2, -1, 1} и 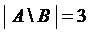 .
.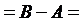 {4, 5} и
{4, 5} и 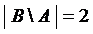 .
.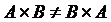 , но при этом
, но при этом 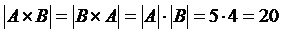 .
.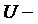 множество сотрудников некоторого предприятия;
множество сотрудников некоторого предприятия; 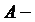 множество всех сотрудников старше 40 лет;
множество всех сотрудников старше 40 лет; 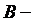 множество сотрудников, имеющих стаж более 10 лет;
множество сотрудников, имеющих стаж более 10 лет; 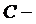 множество служащих;
множество служащих; 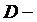 множество рабочих. Каков содержательный смысл каждого из нижеследующих множеств? Изобразить графически (с помощью диаграмм Эйлера – Венна) эти множества.
множество рабочих. Каков содержательный смысл каждого из нижеследующих множеств? Изобразить графически (с помощью диаграмм Эйлера – Венна) эти множества. 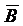 ;
;
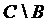 ;
;
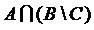 ;
;
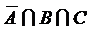 ;
;
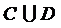 ;
;
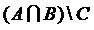 ;
;
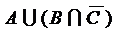 ;
;
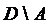 ;
;
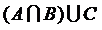 ;
;
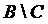 ;
;
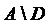 ;
;
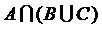 .
.
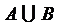 ;
;
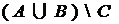 ;
;
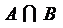 ;
;
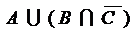 ;
;
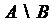 ;
;
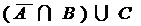 ;
;
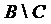 ;
;
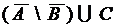 .
.
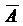 ;
; 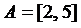 и
и 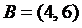 ; 3)
; 3) 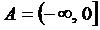 и
и 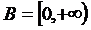 ;
;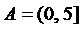 и
и 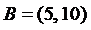 ; 4)
; 4) 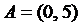 и
и 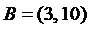
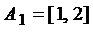 ,
, 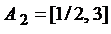 ,
, 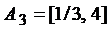 , …,
, …, 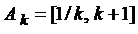 . Найти
. Найти 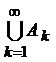 и
и 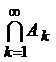 .
. 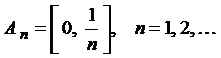 .
.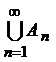 и
и 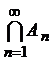 .
. 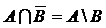 ; 4)
; 4) 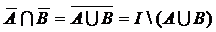 ;
;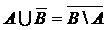 ; 5)
; 5) 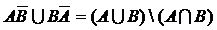 ;
;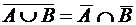 ; 6)
; 6) 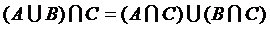 .
.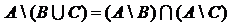 .
.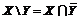 .
.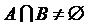 ,
, 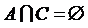 и
и 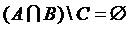 ?
? 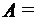 {1, 2, 3},
{1, 2, 3}, 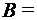 {1, 3, 5},
{1, 3, 5}, 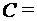 {2, 3, 4, 6}.
{2, 3, 4, 6}.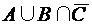 ; 2)
; 2) 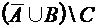 .
.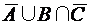 ; 2)
; 2) 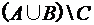 ; 3)
; 3) 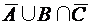 ; 4)
; 4) 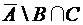 .
.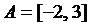 и
и 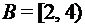 - промежутки на числовой оси. Найти
- промежутки на числовой оси. Найти 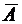 ;
; 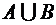 ;
; 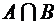 ;
; 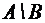 ;
; 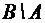 .
.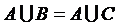 . Можно ли сделать вывод, что В = С ?
. Можно ли сделать вывод, что В = С ?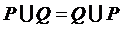 ;
;
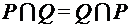 ;
;
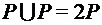 ;
;
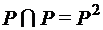 ;
;
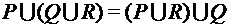 ;
;
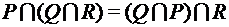 ;
;
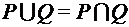 ;
;
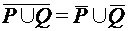 .
.