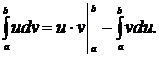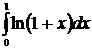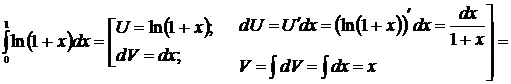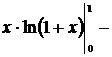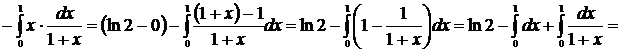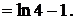Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Метод решения интегралов, содержащих квадратный трёхчлен в знаменателе (задание 4)Найти интеграл, содержащий квадратный трехчлен в знаменателе, результат проверить дифференцированием. Для того, чтобы привести интеграл вида
Затем выражение в скобках необходимо взять за новую переменную. Исходный интеграл при этом сводится к табличному (см. формулы №13-16 таблицы 1). Пример 19 Решение
Проверка
Пример 20 Решение
Проверка
Пример 21 Решение
Проверка
Определённый интеграл и его приложения Основные понятия Пусть на отрезке Сумма Определённым интегралом от функции где
Замечание: определённый интеграл есть число. Свойства определённого интеграла Свойства определённого интеграла аналогичны свойствам неопределённого интеграла. Дополнительные свойства: 1. 2. 3. 4. Пусть функция  Способы вычисления определённого интеграла: 1. Теорема Ньютона-Лейбница. Пусть
Пример 22 Решение
2.Замена переменной. Необходимо вычислить интеграл Пример 23 Решение
3. Формула интегрирования по частям. Пусть Пример 24 Решение
Вычисление площадей плоских фигур (задание 5)
С помощью определенного интеграла вычислить площадь фигуры, ограниченной линиями.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 233. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 или
или  к табличному, следует выделить полный квадрат в квадратном трёхчлене знаменателя. При этом можно использовать формулу
к табличному, следует выделить полный квадрат в квадратном трёхчлене знаменателя. При этом можно использовать формулу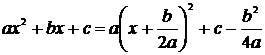 .
.

 [таблица 1, формула №13*]
[таблица 1, формула №13*] 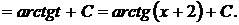


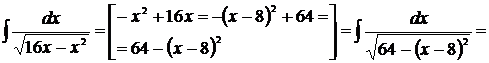
 [таблица 1, формула №15]
[таблица 1, формула №15] 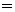
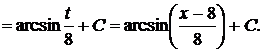
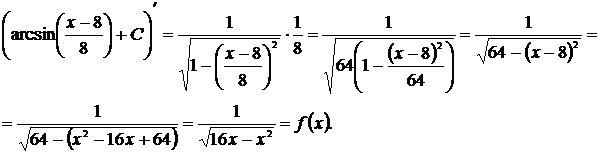
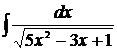


 [таблица 1, формула №16]
[таблица 1, формула №16] 


 задана функция
задана функция  . Разобьём этот отрезок на
. Разобьём этот отрезок на 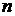 частей точками
частей точками 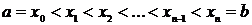 . На каждом малом отрезке
. На каждом малом отрезке  , где
, где 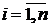 , выберём точку
, выберём точку  , найдём значение функции в этой точке
, найдём значение функции в этой точке 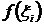 и составим сумму
и составим сумму 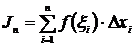 , где
, где  .
. называется интегральной суммой для функции
называется интегральной суммой для функции  на отрезке
на отрезке 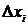 стремится к нулю
стремится к нулю  ,
,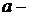 нижний предел интегрирования;
нижний предел интегрирования;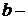 верхний предел интегрирования;
верхний предел интегрирования; подынтегральная функция;
подынтегральная функция; подынтегральное выражение.
подынтегральное выражение. , где
, где 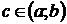 ;
; ;
;
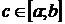 такая, что выполнено равенство
такая, что выполнено равенство  . Здесь
. Здесь 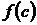 называется средним значением функции.
называется средним значением функции. одна из её первообразных, тогда справедлива формула
одна из её первообразных, тогда справедлива формула


 , где
, где  , полагая
, полагая  . Пусть
. Пусть  , кроме того, при изменении
, кроме того, при изменении  до
до  значения функции
значения функции  не выходят за пределы отрезка
не выходят за пределы отрезка  .
.

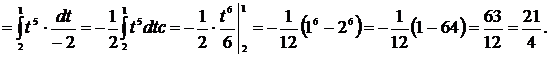
 и
и  - непрерывные функции вместе со своими первыми производными на
- непрерывные функции вместе со своими первыми производными на