Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Перечень ресурсов информационно-коммуникационной сети «Интернет»Правила выполнения и оформления контрольных работ
1. Контрольная работа должна быть выполнена в отдельной тетради в клетку чернилами синего, черного или фиолетового цвета. Необходимо оставлять поля шириной 4 – 5 см для замечаний рецензента. 2. В заголовке работы на обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), номер контрольной работы, название дисциплины; здесь же следует указать название учебного заведения, дату отсылки работы в институт и адрес студента. В конце работы следует поставить дату и расписаться. Студент выполняет те задачи, последняя цифра которых совпадает с последней цифрой его учебного шифра. Например, студент, учебный шифр которого имеет последнюю цифру 0, в контрольной работе решает задачи 10, 20, 30, 40, 50, 60. 3. В работу должны быть включены все задачи, указанные в задании строго по положенному варианту. Контрольные работы, содержащие не все задачи задания, а также задачи не своего варианта, не засчитываются. 4. Решения задач надо располагать в порядке номеров, указанных в заданиях, сохраняя номера задач. Оформление решения каждой задачи начинается с новой страницы. 5. Перед решением каждой задачи надо полностью выписать ее условие. В том случае, если несколько задач, из которых студент выбирает задачи своего варианта, имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными, взятыми из соответствующего номера. 6. Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.  7. После получения прорецензированной работы, как зачтенной, так и незачтенной, студент должен исправить все, отмеченные рецензентом, ошибки и недочеты и выполнить все рекомендации рецензента. Если рецензент предлагает внести в решения задач те или иные исправления или дополнения и прислать их для повторной проверки, то это следует сделать в короткий срок. В случае незачета работы и отсутствия прямого указания рецензента на то, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново. При высылаемых исправлениях должна обязательно находиться прорецензированная работа. Поэтому рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений в соответствии с указаниями рецензента. Вносить исправления в сам текст работы после ее рецензирования запрещается.
§1. Теоретические сведения и типовое решение задач
Задача 1 Даны вершины пирамиды Найти: 1. Длину ребра 2. Угол между ребрами 3. Уравнение грани 4. Уравнения высоты, опущенной из вершины Например:
Решение
Предварительно сделаем рисунок пирамиды: – зафиксируем трехмерное геометрическое пространство с помощью декартовой прямоугольной системы координат и точками отметим вершины пирамиды по их координатам; – соединим вершины пирамиды отрезками прямых; – введем в рассмотрение векторы
Рис.1
1. Длину ребра
2. Для нахождения угла между ребрами Обозначим По определению скалярного произведения: Тогда
Скалярное произведение Подставляя в
Таким образом:
Угол + –
Рекомендуется использовать таблицы ″Брадис В.М. Четырехзначные математические таблицы. – М.: Дрофа, 2004″ или калькулятор.
3. Для составления уравнения грани Из школьного курса математики известно, что плоскость однозначно определена, если заданы её три любые точки. Отсюда следует, что плоскость можно определить с помощью двух векторов, расположенных в плоскости и имеющих общее начало.
Векторы
Выражение 1) тремя точками 2) начальной точной Во втором случае присутствует идея зафиксировать множество точек плоскости посредством системы координат. Смешанное произведение трех векторов находится через координаты перемножаемых сомножителей с помощью определителя 3-го порядка, каждая строка которого состоит из координат соответствующего вектора, поэтому
Раскроем определитель
Обозначим:
тогда
Пусть тогда Уравнение Для числовых данных примера имеем:
Уравнение грани Любая точка этой грани с координатами Для нахождения площади грани
Имеем:
Координаты полученного вектора, который по определению векторного произведения
Площадь грани
4. Чтобы найти уравнения высоты, опущенной из вершины Прямая линия в пространстве, как и на плоскости, однозначно определена, если известны координаты любой одной точки, принадлежащей прямой, а также задан вектор, параллельный прямой. При этом точка называется начальной точкой, а вектор – направляющим вектором прямой.
В качестве начальной точки рассматривается точка
где
Отсюда
Уравнения Если вектор Уравнения высоты, опущенной из вершины
Для данных числового примера уравнения высоты, опущенной из вершины
Определим длину высоты, используя – запишем уравнение высоты в параметрическом виде – подставим – из – обозначим точку пересечения высоты с гранью
– определяем длину высоты по формуле
Ответ: 1. Длина ребра 2. Угол между ребрами 3. Уравнение грани 4. Уравнения высоты, опущенной из вершины
Задача 2
Составить уравнение множества точек, для каждой из которых выполняется следующее условие:
1. Сумма квадратов расстояний до точек 2. Сумма квадратов расстояний до точек 3. Сумма квадратов расстояний до точек 4. Квадрат расстояния до точки 5. Сумма расстояний до точек 6. Квадрат расстояния до точки 7. Сумма квадратов расстояний до сторон прямоугольника, образованного прямыми 8. Расстояние до точки 9. Разность расстояний до точек 10. Расстояние до точки
Решение Линии на плоскости, определяемые алгебраическими уравнениями второй степени относительно координат их точек вида
называются кривыми линиями второго порядка, а уравнения В задаче 2 изучаются кривые линии второго порядка: окружность, эллипс, гипербола, парабола. Каждая линия образуется в соответствии с её определяющим свойством. Логика вывода уравнения линии строится на основе этого свойства.
Окружность: множество точек плоскости, каждая из которых равноудалена от точки плоскости, называемой центром окружности (рис.2).
Рис.2
Основное свойство окружности: Уравнение окружности: где r – радиус. Если центр окружности В Задание уравнения Эллипс: множество точек плоскости, каждая из которых удалена от двух точек плоскости, называемых фокусами эллипса, на равную сумму расстояний (рис.3).
Рис.3
На рис.3:
r
Основное свойство эллипса: Уравнение эллипса: Имеет место соотношение: Если центр эллипса
Гипербола: множество точек плоскости, каждая из которых удалена от двух точек плоскости, называемых фокусами гиперболы, на равную по абсолютной величине разность расстояний (рис.4).
Рис.4
На рис.4:
Основное свойство гиперболы:
Уравнение гиперболы: Имеет место соотношение: При перемещении центра гиперболы Парабола: множество точек плоскости, каждая из которых удалена от точки плоскости, называемой фокусом параболы, на расстояние, равное расстоянию удаления от прямой, называемой директрисой параболы (рис.5).
Рис.5
На рис.5:
Основное свойство параболы:
Уравнение параболы:
где Если вершину параболы переместить в точку Поменяв переменные с осью Уравнения
Уравнение называется общим уравнением окружности, эллипса, гиперболы, параболы. Утверждение: уравнение Перейдем от уравнения
Преобразование
Пусть Здесь: координаты центра окружности Радиус окружности
Пример 1. Составить уравнение множества точек, для каждой из которых сумма квадратов расстояний до точек Решение 1. Обозначим произвольную точку искомого множества точек через Или
2. Приведем это выражение к виду Уравнение 3. По формулам
4. По выражению Выражение
Преобразование
Пусть Получим Здесь: координаты центра эллипса
большая полуось малая полуось
Пример 2. Составить уравнение множества точек для каждой из которых сумма расстояний до точек
Решение 1. Пусть Или
2. Приведем это выражение к виду Уравнение Следовательно, 3. По формулам 4. По выражению Уравнение
Преобразование
Порядок вывода уравнения гиперболы Уравнение
координаты центра гиперболы
действительная полуось
мнимая полуось где
Пример 3. Составить уравнение множества точек, для каждой из которых разность расстояний до точек Решение 1. Пусть Или 2. Приведем это выражение к виду В уравнении 3. По формулам 4. По выражению Уравнение
Преобразование
Имеем 1. Пусть Тогда
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 211. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
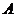
 (
( 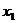 ,
, 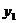 ,
, 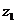 ),
), 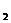 (
( 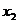 ,
, 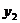 ,
, 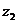 ),
), 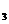 (
( 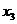 ,
,  ,
, 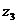 ),
), 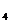 (
(  ,
, 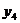 ,
, 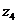 ).
).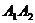 .
.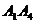 .
.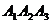 и её площадь.
и её площадь.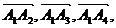 выбирая вершину
выбирая вершину 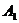 в качестве их общего начала (рис.1).
в качестве их общего начала (рис.1).
 , как расстояния между точками
, как расстояния между точками 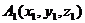 и
и 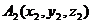 в декартовой прямоугольной системе координат
в декартовой прямоугольной системе координат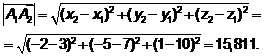

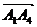 , выраженного через координаты перемножаемых сомножителей.
, выраженного через координаты перемножаемых сомножителей.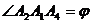 .
.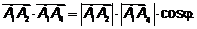 .
. 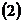
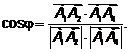 .
. 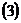
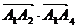 есть сумма произведений одноименных координат перемножаемых векторов:
есть сумма произведений одноименных координат перемножаемых векторов: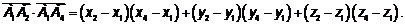 .
. 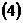
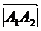 и
и 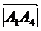 и скалярное произведение
и скалярное произведение 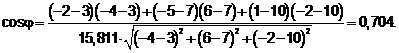
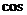
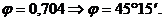
 находим по таблице значений
находим по таблице значений  ,
,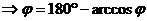 .
.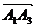 имеют общее начало точку
имеют общее начало точку 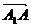 , конец которого точка А является произвольной точкой плоскости. Векторы, располагаемые в одной плоскости, называются компланарными. В соответствии с геометрическим смыслом величина смешанного произведения трех векторов
, конец которого точка А является произвольной точкой плоскости. Векторы, располагаемые в одной плоскости, называются компланарными. В соответствии с геометрическим смыслом величина смешанного произведения трех векторов 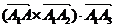 выражает объем параллелепипеда, построенного на этих векторах как на сторонах. Очевидно, что если векторы располагаются в одной плоскости, то объем равен нулю. Таким образом, приравнивая смешенное произведение нулю, получим условие компланарности трех векторов. Учитывая также, что точка
выражает объем параллелепипеда, построенного на этих векторах как на сторонах. Очевидно, что если векторы располагаются в одной плоскости, то объем равен нулю. Таким образом, приравнивая смешенное произведение нулю, получим условие компланарности трех векторов. Учитывая также, что точка 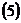
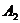 ,
, 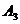 ,
,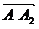 и
и 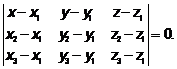 .
. 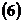
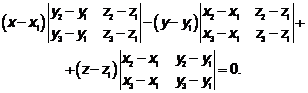 .
.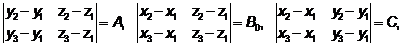
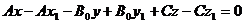 .
.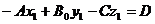 ,
, 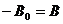 ,
,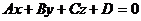 .
. 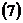

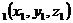 ,
, 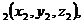
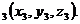 Коэффициенты
Коэффициенты  по своему смыслу суть координаты вектора, нормального к плоскости.
по своему смыслу суть координаты вектора, нормального к плоскости.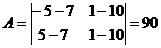
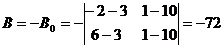
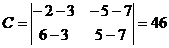
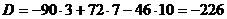
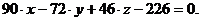
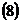
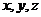 должна удовлетворять уравнению
должна удовлетворять уравнению 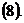
 , равного площади параллелограмма, построенного на векторах
, равного площади параллелограмма, построенного на векторах 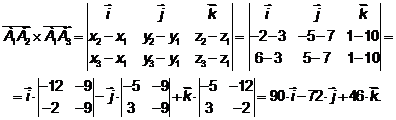
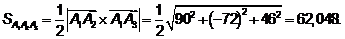
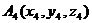 , направляющий вектор представлен вектором
, направляющий вектор представлен вектором 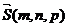 .Возьмем на прямой произвольную точку
.Возьмем на прямой произвольную точку 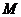 (
( 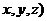 и проведем вектор
и проведем вектор  . Поскольку векторы
. Поскольку векторы 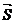 коллинеарны, то
коллинеарны, то 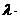
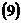
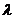 – некоторое действительное число (параметр).
– некоторое действительное число (параметр).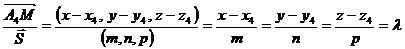 .
. 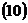
 и
и  , то
, то 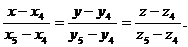
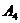 на грань
на грань 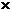
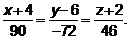 .
. 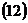
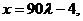
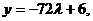
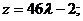

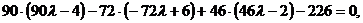
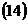
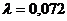 ,
,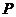 , подставим
, подставим 
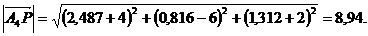
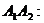
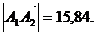
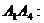
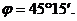
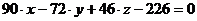 ; площадь грани
; площадь грани 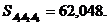
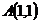 и
и 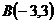 равна 20.
равна 20.
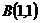 и
и 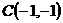 равна 28.
равна 28.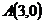 ,
, 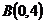 ,
, 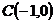 и
и 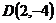 равна 58.
равна 58.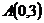 на 3 больше квадрата расстояния до оси абсцисс.
на 3 больше квадрата расстояния до оси абсцисс.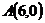 и
и 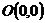 равна 10.
равна 10.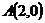 на 16 больше квадрата расстояния до оси ординат.
на 16 больше квадрата расстояния до оси ординат.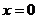 ,
, 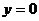 ,
, 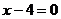 ,
,  , равна 20.
, равна 20.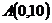 и
и  ,
, 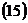
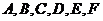 – действительные числа.
– действительные числа.
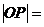 r.
r. 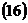
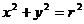 ,
, 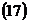
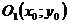 и располагается в первом квадранте, то уравнение окружности
и располагается в первом квадранте, то уравнение окружности 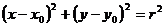 .
. 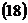
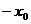 и
и 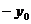 , то центр окружности находится в точке
, то центр окружности находится в точке 
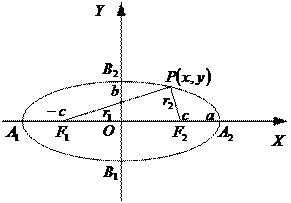
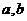 – длины большой и малой полуосей,
– длины большой и малой полуосей,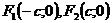 – фокусы эллипса, с – расстояние от центра до фокуса,
– фокусы эллипса, с – расстояние от центра до фокуса, ,
,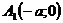 ,
, 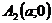 ,
, 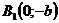 ,
, 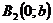 – вершины.
– вершины.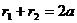 .
. 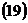
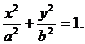
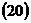
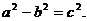
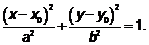 .
. 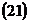
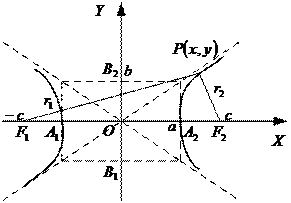
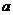 – длина действительной полуоси,
– длина действительной полуоси, 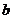 – длина мнимой полуоси,
– длина мнимой полуоси,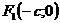 ,
, 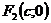 – фокусы гиперболы,
– фокусы гиперболы,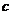 – расстояние от центра до фокуса;
– расстояние от центра до фокуса;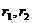 – фокальные радиусы точки
– фокальные радиусы точки 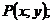
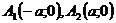 – действительные вершины,
– действительные вершины, – мнимые вершины,
– мнимые вершины,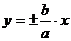 – асимптоты.
– асимптоты.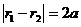 .
. 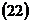
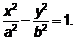
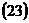
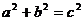 .
.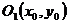 уравнение
уравнение 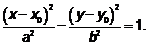
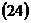
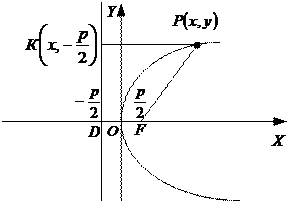
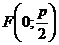 – фокус,
– фокус,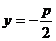 – уравнение директрисы,
– уравнение директрисы,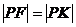 .
. 
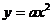 ,
, 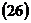
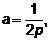 ,
, 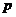 – параметр параболы.
– параметр параболы.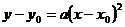 .
. 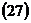
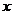 и
и 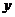 местами, получим уравнение:
местами, получим уравнение: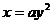 или
или 
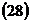
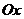 в качестве оси симметрии.
в качестве оси симметрии.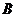 =0
=0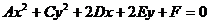
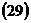
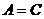 , эллипс при
, эллипс при 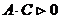 , гиперболу при
, гиперболу при 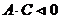 , параболу при
, параболу при 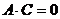 .
.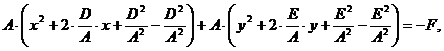
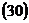
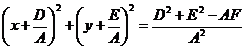 .
.
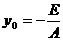 ,
, 
 .
. 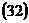
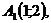
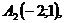
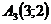 равна
равна 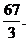
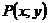 и запишем её заданное свойство
и запишем её заданное свойство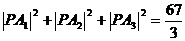 .
.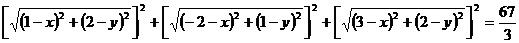 .
.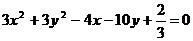 .
. 
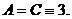 Следовательно,
Следовательно, 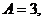
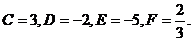
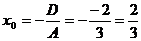 ,
,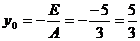 ,
,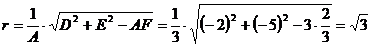 .
.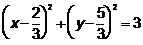 .
. 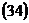
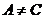 ,
, 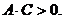
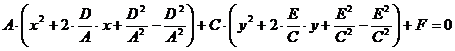 ,
,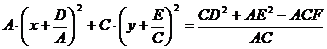 ,
, .
. 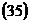
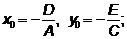
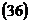
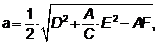 ,
, 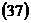
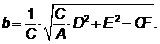 .
. 
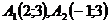 равна 5.
равна 5.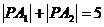 .
. .
. .
. 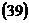
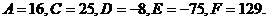
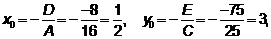
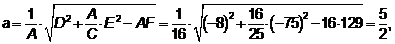 ,
,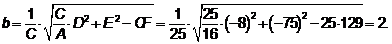 .
.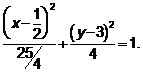
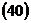
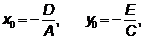
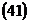
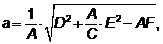 ,
, 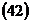
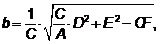 ,
, 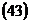
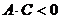 .
.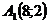 и
и 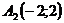 равна 8.
равна 8.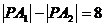 .
. .
. 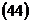
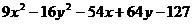 ,
,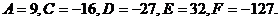
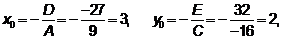
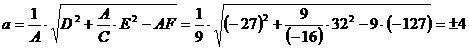 ,
,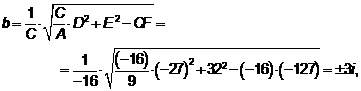 ,
,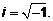 .
.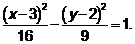 .
. 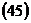
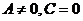 .
.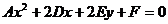 ,
, 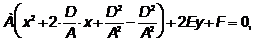 ,
,