
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Равномощность множеств. Кардинальные числа.
Введем понятие равномощности множеств, одно из самых интересных и важных понятий теории множеств. Определение. Два множества Пример 1. Если Пример 2. Пусть Функция Терема 1. Для произвольных множеств (I) Д о к а з а т е л ь с т в о. Равномощность множества Если функция Если функция Верны следующие формулы:
Мы опускаем доказательства (2-7), т.к. они не сложны (смотреть Е. Смупецкий, Л. Борковский «Элементы математики и теории множеств»). Докажем формулы (8-10). Пусть  Для каждого фиксированного Если Каждая функция Таким образом, сопоставляя функции Чтобы доказать (9), заметим, что если Отсюда следует, что Легко убедиться, что, сопоставляя функциям Наконец, чтобы доказать (10), сопоставим каждой функции Формулы (2) и (8-10) представляют собой частные случаи следующих теорем. Теорема 2 (закон коммутативности). Пусть Д о к а з а т е л ь с т в о. Сопоставим каждой функции 1) Таким образом, соответствие, установленное равенстом 2) Функция 3) Наконец, каждую функцию, принадлежащую декартову произведению Теорема 3 (закон ассоциативности). Пусть
Д о к а з а т е л ь с т в о. Обозначим Сопоставим функции
где Областью определения этой функции служит множество 1) Отображение, сопоставляющее функциям 2) Осталось показать, что каждая функция Для доказательства (13) достаточно в (12) положить Теорема 4 (Закон возведения в степень декартова произведения). Пусть
Д о к а з а т е л ь с т в о. Зададим на множестве Декартово произведение можно представить в виде суммы попарно непересекающихся множеств двумя различными способами :
где
Например,
Аналогично Дважды применяя теорему 3, получим
Для
Из (15) получаем
Сопоставляя при данном
Формула (14) непосредственно следует из (17) и (18). Если множества ( a) качества ??? элементов множества b) от их порядка.
Разумеется ???, этим не оправдывается понятие мощности множества или его кардинального числа, а только вводится новый термин для понятия равномощности. В конечном счете этот термин не обязателен, поскольку теоремы теории множеств можно сформулировать так, чтобы в них шла речь не о свойствах кардинального числа (или мощности), а об отношениях между ними, и эти отношения всегда можно доказать при помощи понятия равномощности. Однако многие теоремы теории множеств становятся более обозримыми, если они сформулированы как теоремы о кардинальных числах. Это и оправдывает введение в теорию множеств кардинальных чисел. Легко доказывается Теорема 5. Для того, чтобы множество Реляционный тип системы Из теоремы 5 и аксиомы VIII (§ 10, глава II) вытекает Теорема 6. Для произвольных множеств Эта теоремы позволяет представить результаты о равномощности множеств в виде равенств кардинальных чисел.
Счетные множества.
Пусть В дальнейшем кардинальное число конечного множества будем отождествлять с числом его элементов. Таким ообразом, теория мощностей конечных множеств не выводит нас за рамки арифметических натуральных чисел. Новые ситуации возникают только тогда, когда мы переходим к рассмотрению бесконечных множеств. О п р е д е л е н и е. Множество Очевидно, что любые два бесконечные счетные множества равномощны (смотреть теорему 1, § 1). Кардинальное число бесконечных счетных множеств обозначим через а ( В главе III мы определили последовательность как функцию, областью определения которой служит множество натуральных чисел. Из этого определения следует, что бесконечное множество Допуская некоторую вольность, можно сказать, что множество Теорема 1. Каждое непустое счетное множество является множеством значений некоторой бесконечной последовательности. И обратно, множество значений произвольной бесконечной последовательности счетно и непусто. Д о к а з а т е л ь с т в о. Конечное множество
Бесконечное счетное множество есть по определению множество значений некоторой бесконечной последовательности. Для доказательства обратного утверждения рассмотрим множество Пусть По индукции легко доказать, что для каждого Предположим, что множество Если Наименьшее такое число По определению последовательности Аналогично доказывается |
||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 320. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
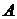 и
и  равномощны, если существует взаимно однозначная функция
равномощны, если существует взаимно однозначная функция  с областью определения
с областью определения  и говорят, что
и говорят, что  имеет столько же элементов, что и
имеет столько же элементов, что и  ,
, .
. взаимно однозначна и отображает множество
взаимно однозначна и отображает множество  .
.
 (теорема 4 , §6, глава II).
(теорема 4 , §6, глава II). устанавливает равномощность множеств
устанавливает равномощность множеств 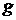 - равномощность множеств
- равномощность множеств  устанавливает равномощность множеств
устанавливает равномощность множеств 
 ,
, 


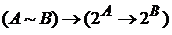

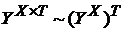


 , т.е.
, т.е. 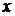 и
и  (первая пробегает множество
(первая пробегает множество  , вторая – множество
, вторая – множество 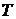 ), значения которой принадлежат
), значения которой принадлежат  .
. (одной переменной
(одной переменной  , отображает
, отображает 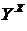 . Функция
. Функция 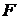 , определенная равенством
, определенная равенством  , ставит в соответствие каждому
, ставит в соответствие каждому 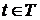 элемент множества
элемент множества  .
. и
и 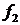 - две различные функции, принадлежащие множеству
- две различные функции, принадлежащие множеству  , то соответсвующие им функции
, то соответсвующие им функции  и
и  также различны. В самом деле, если
также различны. В самом деле, если  , то элементы
, то элементы  и
и  множества
множества  , где
, где  .
. , т.е. формула (8) верна.
, т.е. формула (8) верна. , то
, то  для каждого
для каждого  является упорядоченной парой
является упорядоченной парой  , где
, где  ,
,  .
. ,
,  .
. , мы устанавливаем взаимно однозначное отображение множества
, мы устанавливаем взаимно однозначное отображение множества  на множество
на множество  .
. уорядоченную пару сужений
уорядоченную пару сужений 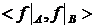 . Легко убедиться, что при этом множество
. Легко убедиться, что при этом множество  взаимно однозначно отображается на
взаимно однозначно отображается на  .
. . Если
. Если 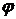 - перестановка множества
- перестановка множества  (11)
(11)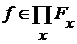 суперпозицию
суперпозицию  . Если
. Если  , то
, то  для некоторого
для некоторого  , получаем
, получаем 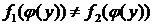 или
или  .
. . В самом деле, если
. В самом деле, если  , т.е.
, т.е.  .
. , где
, где  .
. и все множества
и все множества  попарно не пересекаются, то
попарно не пересекаются, то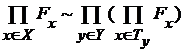 (12)
(12) (13)
(13)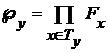 . Это множество таких функций
. Это множество таких функций  , если
, если  . Множество
. Множество 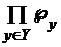 состоит, в свою очередь, из таких функций
состоит, в свою очередь, из таких функций  , если
, если  . Значение
. Значение  функции
функции  . Это такая функция с областью определения
. Это такая функция с областью определения  .
. функцию
функцию  (*),
(*), - тот элемент множества
- тот элемент множества  .
. , то существует такая
, то существует такая  , что
, что  , и поэтому существует такой элемент
, и поэтому существует такой элемент  . Тогда в силу (*)
. Тогда в силу (*)  .
. , принадлежит декартову произведению
, принадлежит декартову произведению  и удовлетворяет равенству (*).
и удовлетворяет равенству (*). для каждого
для каждого  . Тогда для каждого множества
. Тогда для каждого множества 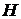
 (14).
(14). функцию
функцию 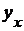 равенством
равенством  .
.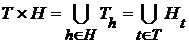 ,
, - множество всех пар со вторым элементом
- множество всех пар со вторым элементом  ,
, - множество всех пар с первым элементом
- множество всех пар с первым элементом  .
. ,
, .
. (15)
(15) (16)
(16) имеем
имеем 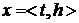 и, значит,
и, значит,  , откуда :
, откуда : . Т.к.
. Т.к.  , то :
, то : 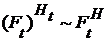 ,
, 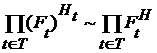 .
.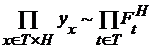 (17).
(17). функции
функции  функцию
функцию  , убеждаемся, что
, убеждаемся, что  , а в силу (16) :
, а в силу (16) : (18).
(18).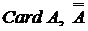 ) .
) . - Кантор определял (???) мощность множества
- Кантор определял (???) мощность множества  - двойное отрицание подчеркивает этот двойной акт абстрагирования.
- двойное отрицание подчеркивает этот двойной акт абстрагирования. и
и  были изоморфны.
были изоморфны. эквивалентны.
эквивалентны. элементов, тогда теорема 6 § 1 выполняется, если положить
элементов, тогда теорема 6 § 1 выполняется, если положить  .
.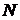 - мощность радя натуральных множеств).
- мощность радя натуральных множеств). .
. есть множество значений бесконечной последовательности.
есть множество значений бесконечной последовательности. .
. и
и  , где
, где 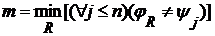 или же
или же  , если нет такого
, если нет такого  , что
, что  .
. и, таким образом, все числа последовательности
и, таким образом, все числа последовательности 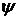 различны. Осталось показать, что каждый элемент множества
различны. Осталось показать, что каждый элемент множества 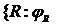 не является членом последовательности
не является членом последовательности  - наименьший его элемент. Очевидно, что
- наименьший его элемент. Очевидно, что  .
. , то
, то  - член последовательности
- член последовательности  . Пусть
. Пусть  .
. , как раз и равно
, как раз и равно  , что противоречит выбору
, что противоречит выбору