Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Понятие и вычисление определителя матрицыСтр 1 из 5Следующая ⇒ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования РОССИЙСКИЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ Им. Г.В. ПЛЕХАНОВА Воронежский филиал Отделение среднего профессионального и дополнительного образования
МАТЕМАТИКА
Методическое пособие и задания для контрольной работы для студентов второго курса специальности 38.02.01 «Экономика и бухгалтерский учёт (по отраслям)» очной формы обучения
Воронеж 2017 СОДЕРЖАНИЕ Введение……………………………………………………………………….. 4 Примерный тематический план……………………………………………. 5 Общие методические указания по выполнению контрольной работы.. 6 Краткие теоретические сведения и образцы решения задач…………… 7 Раздел 1. Элементы линейной алгебры. …………………………………… .. 7 Матрицы и определители……………………………………………………. 7 Системы линейных уравнений …………………………………………….. 12 Раздел 2. Основы математического анализа……………………………… .. 13 Теория пределов ……………………………………………………………. 13 Дифференциальное исчисление……………………………………………. 18 Интегральное исчисление………………………………………………….. 20 Раздел 3. Основы теории комплексных чисел………………………………. 26 Раздел 4. Элементы теории вероятностей и математической статистики…. 30 Задания контрольной работы………………………………………………. 34 Рекомендуемая литература…………………………………………………. 38 Приложения …………………………………………………………………… 39

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ И ОБРАЗЦЫ РЕШЕНИЯ ЗАДАЧ Раздел 1. Элементы линейной алгебры Матрицы Матрицей размером Если элементамиматрицы являются числа, то она называется числовой матрицей. Элементы матрицы удобно снабжать двумя индексами Главной диагональю квадратной матрицы называют диагональ, идущую из левого верхнего в правый нижний угол. Квадратная матрица, у которой все элементы, лежащие ниже или выше главной диагонали, равны нулю, называется треугольной матрицей. Квадратная матрица, у которой все элементы, кроме элементов, стоящих на главной диагонали, равны нулю, называется диагональной матрицей. Например, Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой
Действия с матрицами Пусть матрицы Если в матрице Например, для матрицы Если матрицы Примеры. Найти сумму матриц: a) b) Сложение матриц подчиняется следующим законам: a) коммутативному b) ассоциативному Для того чтобы умножить матрицу Для любых чисел 1. 2. 3. Пример. Найти
Для матриц, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй) вводится операция умножения матриц. Произведением матрицы Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат. Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Например, Матрицы не перестановочны друг с другом, т.е.
Произведение 2-х ненулевых матриц может оказаться равным нулевой матрице. Например, . Понятие и вычисление определителя матрицы Определителем квадратной матрицы порядка
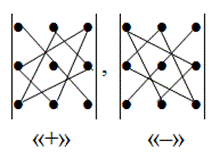
Итак, для того чтобы найти определитель второго порядка нужно из произведения элементов главной диагонали вычесть произведение элементов второй диагонали. Пример. Вычислить определители второго порядка Определителем третьего порядка, соответствующим данной квадратной матрице третьего порядка, будет число, получаемое следующим образом: При вычислении определителей третьего порядка удобно пользоваться правилом треугольников. Схематически это правило можно изобразить следующим образом:
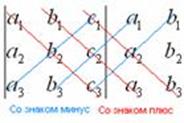
Три положительных члена определителя представляют собой произведения элементов главной диагонали и элементов, находящихся в вершинах двух равнобедренных треугольников, основания которых параллельны главной диагонали. Три отрицательных его члена есть произведения элементов побочной диагонали и элементов, находящихся в вершинах двух равнобедренных треугольников, основания которых параллельны побочной диагонали. Пример. Для нахождения определителя третьего порядка часто используют способ Саррюса или способ «параллельных полосок» Суть состоит в том, что справа от определителя приписывают первый и второй столбец и проводят параллельные линии:
Множители, находящиеся на диагоналях, параллельных главной диагонали входят в формулу со знаком «плюс». Множители, находящиеся на диагоналях, параллельных побочной диагонали входят в формулу со знаком «минус». Свойства определителя матрицы 1. Определитель единичной матрицы равен единице 2. Определитель матрицы с двумя равными строками (столбцами) равен нулю. 3. Определитель матрицы с двумя пропорциональными строками (столбцами) равен нулю. 4. Определитель матрицы, содержащий нулевую строку (столбец), равен нулю. 5. Определитель матрицы равен нулю если две (или несколько) строк (столбцов) матрицы линейно зависимы. 6. При транспонировании значение определителя матрицы не меняется 7. Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить другую строку (столбец), умноженную на некоторое число. 8. Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить линейную комбинации других строк (столбцов). 9. Если поменять местами две строки (столбца) матрицы, то определитель матрицы поменяет знак. 10. Общий множитель в строке (столбце) можно выносить за знак определителя 11. Если квадратная матрица n-того порядка умножается на некоторое ненулевое число, то определитель полученной матрицы равен произведению определителя исходной матрицы на это число в n-той степени 12. Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем 13. Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов 14. Определитель произведения матриц равен произведению определителей этих матриц. Обратная матрица Матрица Обратная матрица обозначается Минором -ого порядка матрицы Минор Например, для матрицы Алгебраическим дополнением элемента Алгебраическое дополнение элемента Алгоритм нахождения обратной матрицы 1. Найти определитель матрицы 2. Найти алгебраические дополнения элементов матрицы. 3. Составить матрицу 4. Разделить присоединённую матрицу на детерминант. Полученная матрица будет обратной Пример. Найти матрицу, обратную матрице
Находим алгебраические дополнения Матрица из алгебраических дополнений имеет вид
Системы линейных уравнений Правило Крамера Рассмотрим систему двух линейных уравнений с двумя неизвестными Решая данную систему способом сложения, получим,
В полученной системе коэффициенты при переменных равны определителю второго порядка, составленному из коэффициентов при переменных системы, а свободные члены получены из данного определителя; первый - заменой элементов первого столбца свободными членами Введём обозначения;
Система запишется в виде Исследуем полученную систему. 1) Если 2) Если 3) Если Метод Крамера можно обобщить на систему Теорема Система
Таким образом, для решения системы · главный определитель, составленный из коэффициентов при неизвестных; · дополнительный определитель для первой переменной, полученный из главного определителя заменой чисел первого столбца на свободные члены; · дополнительный определитель для второй переменной, полученный из главного определителя заменой чисел второго столбца на свободные члены; · дополнительный определитель для третьей переменной, полученный из главного определителя заменой чисел третьего столбца на свободные члены и т. д. · дополнительный определитель для · для получения значений неизвестных требуется разделить значения дополнительных определителей на главный определитель
Пример 1. Решение: 1) Составим и вычислим главный определитель 2) Составим и вычислим определитель 3) Составим и вычислим определитель 4) Найдем значения Ответ: Пример 2.
Так как
Проверка:
Метод Гаусса Если 1. Умножение обеих частей уравнений на одно и то же число; 2. Прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на некоторое число. Если в процессе решения системы появится уравнение вида Алгоритм метода Гаусса 1. Выбирают в системе одно уравнение, которое называют ведущим или разрешающим уравнением 2. В этом уравнении выбирают одну неизвестную, коэффициент которой отличен от нуля. Переменную называют ведущей или разрешающей переменной. 3. Подбирают числовые множители для каждого из уравнений так, чтобы после сложения ведущего уравнения с каждым из других уравнений системы, в них «пропала» ведущая переменная 4. В полученной после сложения системе выбирают подсистему, в которой на одно уравнение и на одну переменную меньше 5. Для подсистемы снова выполняют пункты 1-4. В результате система сведётся к одному из следующих случаев a. Система принимает «треугольный» вид, в котором последнее уравнение содержит только одну переменную, предпоследнее уравнение содержит только две неизвестные и т. д. После приведения системы к «треугольному» виду, неизвестные находят одна за другой методом подстановки. Система будет иметь единственное решение. b. Система принимает «трапецеидальный» вид, в которой последнее уравнение содержит наименьшее количество переменных, но не одну. После приведения системы к «трапецеидальному» виду «треугольную» часть системы оставляют в левой стороне, а неизвестные, не вошедшие в «треугольник», переносят в правую часть системы, выражая через них остальные переменные. «Лишние» неизвестные могут принимать любые значения, и система будет иметь бесконечно много решений c. Система противоречива, противоречие становится очевидным на каком-то шаге. Система в этом случае решений не имеет.
Пример 1. Решить методом Гаусса систему уравнений:
Первое уравнение системы считаем ведущим, неизвестную
Выбираем второе уравнение системы и неизвестную Из последнего уравнения полученной системы следует, что Пример 2. Решить методом Гаусса систему уравнений:
Считаем первое уравнение и первую переменную за ведущие. Умножая первое уравнение на
«Треугольную» часть системы оставляем в левой части, а остальную часть переносим в правую часть системы.
Подставляя значения для
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 228. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
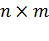 называется прямоугольная таблица каких-либо данных, состоящая из
называется прямоугольная таблица каких-либо данных, состоящая из 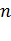 строк и
строк и 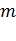 столбцов. Данные, составляющие матрицу, называются элементами матрицы. Матрицу обычно заключают в круглые скобки и обозначают прописными латинскими буквами
столбцов. Данные, составляющие матрицу, называются элементами матрицы. Матрицу обычно заключают в круглые скобки и обозначают прописными латинскими буквами 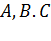 и т. д. Когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. В общем виде матрицу размером
и т. д. Когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. В общем виде матрицу размером 
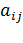 : первый указывает номер строки, а второй – номер столбца. Например,
: первый указывает номер строки, а второй – номер столбца. Например, 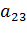 – элемент стоит во 2- ой строке, 3-м столбце. Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число её строк или столбцов называется порядком матрицы. Например, в матрице
– элемент стоит во 2- ой строке, 3-м столбце. Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число её строк или столбцов называется порядком матрицы. Например, в матрице 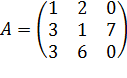 три строки и три столбца;
три строки и три столбца; 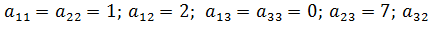 =6. В данной матрице количество строк совпадает с количеством столбцов, поэтому она квадратная, третьего порядка. Матрица, у которой всего одна строка, называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом. Такие матрицы также называют векторами. Например,
=6. В данной матрице количество строк совпадает с количеством столбцов, поэтому она квадратная, третьего порядка. Матрица, у которой всего одна строка, называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом. Такие матрицы также называют векторами. Например, 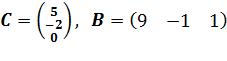
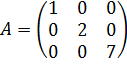 .
.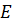 . Например, единичная матрица 3-го порядка имеет вид:
. Например, единичная матрица 3-го порядка имеет вид: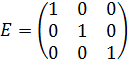
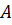 и
и 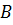 состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы
состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы 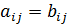 . Так если
. Так если  и
и 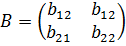 , то
, то 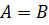 , если
, если 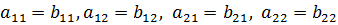
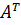 .
.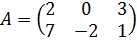 транспонированной матрицей будет
транспонированной матрицей будет  .
.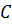 , которая определяется по правилу, например,
, которая определяется по правилу, например, 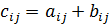 , т. е., для того, чтобы сложить матрицы
, т. е., для того, чтобы сложить матрицы  и
и 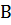 нужно к элементам матрицы
нужно к элементам матрицы 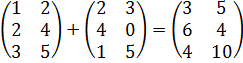
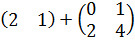 . Сложить нельзя, т.к. размеры матриц различны.
. Сложить нельзя, т.к. размеры матриц различны.
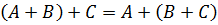 .
.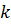 нужно каждый элемент матрицы
нужно каждый элемент матрицы 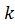 есть новая матрица, которая определяется по правилу
есть новая матрица, которая определяется по правилу 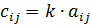
 , и матриц
, и матриц 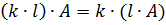
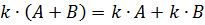
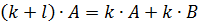
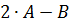 , если,
, если, 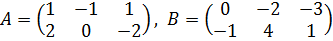
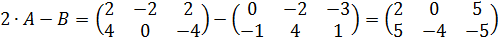
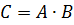 , элементы которой составляются следующим образом: чтобы получить у произведения элемент, стоящий в 1-ой строке и 1 -м столбце, нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 1-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. Второй элемент первой строки матрицы - произведения получается аналогично. Элементы первой строки первой матрицы умножаются на соответствующие элементы второго столбца второй матрицы, и полученные произведения складываются и т. д. Для получения элементов второй строки матрицы-произведения те же самые операции повторяются для второй строки первой матрицы и столбцов второй матрицы. Элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы.
, элементы которой составляются следующим образом: чтобы получить у произведения элемент, стоящий в 1-ой строке и 1 -м столбце, нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 1-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. Второй элемент первой строки матрицы - произведения получается аналогично. Элементы первой строки первой матрицы умножаются на соответствующие элементы второго столбца второй матрицы, и полученные произведения складываются и т. д. Для получения элементов второй строки матрицы-произведения те же самые операции повторяются для второй строки первой матрицы и столбцов второй матрицы. Элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы. . Пример. Найти произведение матриц.
. Пример. Найти произведение матриц. 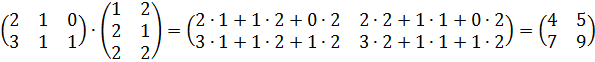 .
.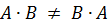 . Поэтому при умножении матриц нужно тщательно следить за порядком множителей. Умножение матриц подчиняется ассоциативному и дистрибутивному законам, т.е.,
. Поэтому при умножении матриц нужно тщательно следить за порядком множителей. Умножение матриц подчиняется ассоциативному и дистрибутивному законам, т.е., 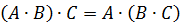 и
и 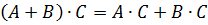 . При умножении квадратной матрицы
. При умножении квадратной матрицы 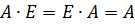 .
.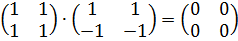
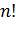 слагаемых. Каждое слагаемое представляет собой произведение
слагаемых. Каждое слагаемое представляет собой произведение 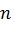 элементов матрицы, причём в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы
элементов матрицы, причём в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы  . Перед слагаемым появляется коэффициент (-1), если элементы матрицы
. Перед слагаемым появляется коэффициент (-1), если элементы матрицы 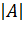 , также встречается обозначение
, также встречается обозначение 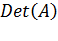 или
или 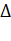 . Также определитель называют детерминантом. Пусть дана матрица второго порядка – квадратная матрица, состоящая из двух строк и двух столбцов,
. Также определитель называют детерминантом. Пусть дана матрица второго порядка – квадратная матрица, состоящая из двух строк и двух столбцов, 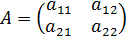 . Определителем второго порядка, соответствующим данной матрице, будет число, получаемое следующим образом
. Определителем второго порядка, соответствующим данной матрице, будет число, получаемое следующим образом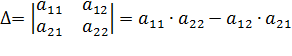 .
.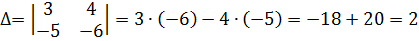 .
.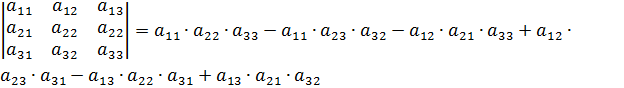
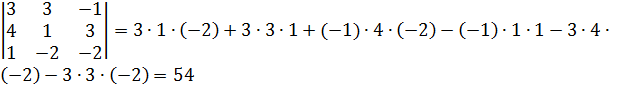 .
.
 , где
, где  .
.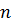 на
на 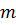 – это определитель матрицы порядка
– это определитель матрицы порядка 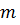 или
или 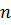 ).
).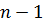 -ого порядка квадратной матрицы
-ого порядка квадратной матрицы 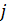 -ого, обозначим как
-ого, обозначим как  . Иными словами, минор
. Иными словами, минор 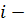 ой строки и
ой строки и 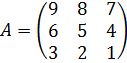 найдём
найдём 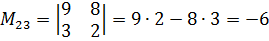 .
.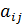 квадратной матрицы
квадратной матрицы 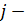 ого столбца, умноженный
ого столбца, умноженный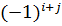 .
.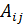 . Таким образом,
. Таким образом, 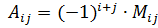 . Например, для матрицы
. Например, для матрицы 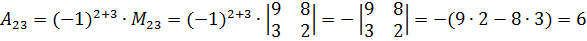 .
. из алгебраических дополнений элементов матрицы
из алгебраических дополнений элементов матрицы 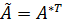 .
.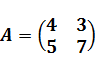 .
.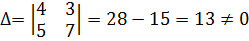 . Значит, обратная матрица существует.
. Значит, обратная матрица существует.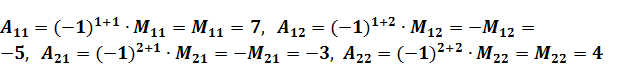
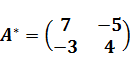 . Присоединённая матрица
. Присоединённая матрица  . Находим обратную матрицу по формуле
. Находим обратную матрицу по формуле 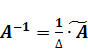 =
= 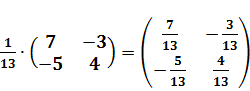

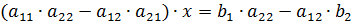

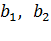 системы, а второй – заменой элементов второго столбца определителя теми же свободными членами.
системы, а второй – заменой элементов второго столбца определителя теми же свободными членами.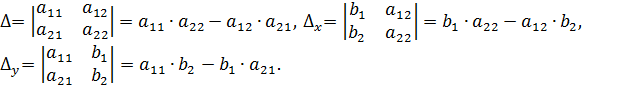
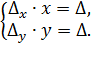
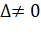 , то система имеет единственное решение:
, то система имеет единственное решение: 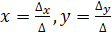 . Эти формулы называются формулами Крамера.
. Эти формулы называются формулами Крамера.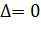 , а
, а 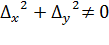 , то система не имеет решений.
, то система не имеет решений. , то система имеет бесконечное множество решений.
, то система имеет бесконечное множество решений.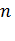 неизвестными:
неизвестными: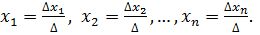
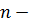 ой переменной, полученный из главного определителя заменой чисел
ой переменной, полученный из главного определителя заменой чисел 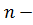 го столбца на свободные члены
го столбца на свободные члены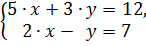
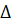 :
: 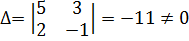 - система имеет одно решение, можно применить теорему Крамера
- система имеет одно решение, можно применить теорему Крамера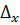 :
: 
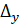 :
: 
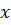 и
и 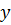 по формулам Крамера
по формулам Крамера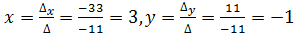 .
.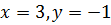
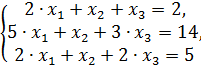 .
. 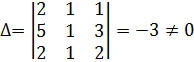
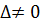 , то система имеет единственное решение. Вычислим вспомогательные определители.
, то система имеет единственное решение. Вычислим вспомогательные определители.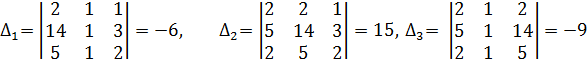
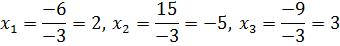
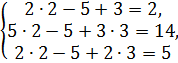
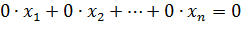 , то оно отбрасывается из полученной системы. Если же среди уравнений системы окажется уравнение вида
, то оно отбрасывается из полученной системы. Если же среди уравнений системы окажется уравнение вида 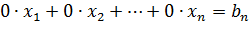 , где
, где 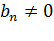 , то такая система не имеет решений.
, то такая система не имеет решений.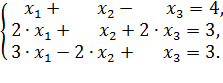
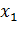 считаем ведущей. Умножая первое уравнение последовательно на
считаем ведущей. Умножая первое уравнение последовательно на 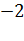 и на
и на 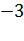 , и прибавляя его соответственно ко второму и третьему уравнениям, получаем систему:
, и прибавляя его соответственно ко второму и третьему уравнениям, получаем систему: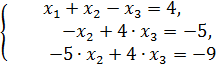
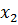 ведущими. Умножая ведущее уравнение на
ведущими. Умножая ведущее уравнение на 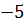 , и прибавляя его к третьему уравнению, приходим к системе:
, и прибавляя его к третьему уравнению, приходим к системе: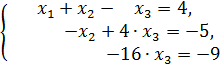
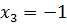 . Найденное значение подставляем в предшествующее уравнение системы (второе). Получаем
. Найденное значение подставляем в предшествующее уравнение системы (второе). Получаем 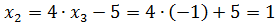 . Найденные значения
. Найденные значения 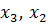 подставляем в предшествующее уравнение системы (первое). Получаем:
подставляем в предшествующее уравнение системы (первое). Получаем: 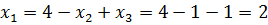 .
.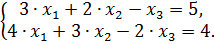
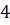 , а второе на
, а второе на 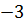 и складывая их, приходим к системе «трапецеидального» вида.
и складывая их, приходим к системе «трапецеидального» вида.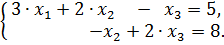
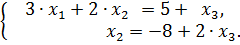
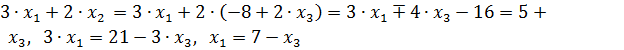 . Система имеет бесконечно много решений,
. Система имеет бесконечно много решений,