
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Приближение линейными сплайнами
Пусть m = 1 . Тогда общее число Q свободных параметров равно 2N . Поставим вопрос о построении сплайна
Получим систему уравнений
Эта система распадается на системы уравнений относительно коэффициентов отдельных многочленов
отсюда находим
Многочлен Pn1(x) является многократно рассматривавшимся интерполяционным многочленом первой степени с узлами интерполяции xn-1, xn. Широкое распространение сплайнов во многом вызвано тем, что они являются в определенном смысле наиболее гладкими функциями среди функций, принимающих заданные значения. Сплайны степени выше первой в случае гладкой f(x) хорошо приближают не только саму функцию, но и ее производные.
ЛЕКЦИЯ 9. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ Известно, что не для всякой функции ее первообразная выражается через элементарные функции. В этих случаях вычисление определенных интегралов по формуле Ньютона-Лейбница затруднительно и применяются различные методы приближенного вычисления определенных интегралов. Пользуясь геометрическим смыслом определенного интеграла, рассмотрим три приближенных формулы, с помощью которых численное интегрирование проводится с любой степенью точности.
Постановка задачи Пусть на отрезке [a,b] задана непрерывная функция y = f(x). Требуется вычислить приближенное значение определенного интеграла
 Воспользуемся этой интерпретацией определенного интеграла. Разобьем отрезок [a,b] точками a = х0, х1, ..., хn = b на n равных частей длины
Величина h называется шагом интегрирования. Обозначим через у0, у1, …, уn значения функции y = f(x) в точках х0 , х1...., хn соответственно, то есть yi = f(xi),
Формула прямоугольников Заменим площадь криволинейной трапеции aАВb (рис. 9.2), численно равную интегралу (9.1), на сумму площадей левосторонних или правосторонних прямоугольников, то есть на y0h + y1h + … + yn-1 h или y1h + y2h + … + ynh. Тогда интеграл (9.1) приближенно выражается любой из формул:
Это формулы левосторонних и правосторонних прямоугольников.
где
то для интеграла (1) получаем приближенную формулу
Это формула трапеций. Число n произвольно, но чем оно больше, тем с большей точностью будет получено значение интеграла (9.1). Если f"(x) существует и ограничена на отрезке [a,b], то погрешность Rn формулы (9.5) оценивается неравенством
9.4. Формула парабол (Формула Симпсона).Разделим отрезок [a, b] на четное число равных частей n = 2m. Площадь криволинейной трапеции, соответствующей первым двум отрезкам [х0, х1] и [х1, х2] и ограниченной заданной кривой y = f(x), заменим площадью параболической трапеции, которая ограничена параболой, проходящей через три точки М0(х0, у0), М1(х1, у1), М2(х2, у2), и имеющей ось, параллельную оси Оу (рис. 9.4). Аналогичным образом поступим и для других пар отрезков [х2, х3], [х3, х4], …, [х2m-2, х2m-1], [х2m-1, х2m]. Площади построенных параболических трапеций соответственно равны
а их сумма даст приближенное значение интеграла (9.1)
Это формула Симпсона. Здесь число 2m точек деления отрезка [a,b] произвольно, но чем больше это число, тем точнее значение интеграла (9.1). Если f"(x) существует и ограничена на отрезке [a,b], то для погрешности Rnформулы (9.8) справедлива следующая оценка:
где
ЗАМЕЧАНИЕ. В связи с трудностями оценки четвертой производной подынтегральной функции f(x), погрешность Rn совершаемую при вычислении определенного интеграла (9.1), по формуле (9.8), можно оценить по правилу Рунге
где Jn и J2n – приближенное значение интеграла, вычисленное по формуле парабол, соответственно с шагом h и
ЛЕКЦИЯ 10. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Невелико число типов дифференциальных уравнений, допускающих решение в квадратурах (сведение к дифференциальному уравнению с разделяющими переменными с последующим интегрированием). Многообразие видов уравнений, встречающихся при решении физических и технических вопросов, привело к созданию большого числа методов приближенного решения дифференциальных уравнений, основанных на самых различных идеях. Все эти методы в зависимости от формы, в которой они представляют решение, можно разделить на три основные группы: 1. Аналитические методы, дающие приближенное решение дифференциального уравнения в виде аналитического выражения; 2. Графические методы, дающие приближенное решение в виде графиков. 3. Численные методы, дающие приближенное решение в виде таблицы. Остановимся на численных методах.
|
||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 257. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
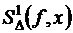 совпадающего с функцией f(x) в точках x0, x1,…, xn .
совпадающего с функцией f(x) в точках x0, x1,…, xn .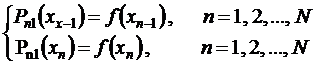
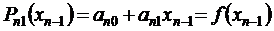 ,
,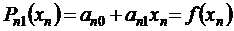


 (9.1)
(9.1)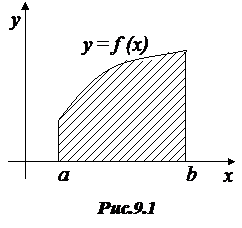 Если f(x) ≥ 0 при a ≤ х ≤ b,то интервал будет численно равен площади так называемой криволинейной трапеции, ограниченной графиком функции y = f(x), прямыми х = a, х = b и осью Ох (рис.9.1).
Если f(x) ≥ 0 при a ≤ х ≤ b,то интервал будет численно равен площади так называемой криволинейной трапеции, ограниченной графиком функции y = f(x), прямыми х = a, х = b и осью Ох (рис.9.1).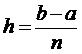 , так что xi = a + ih,
, так что xi = a + ih, 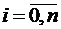 .
.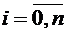 .
.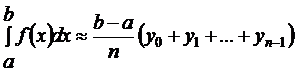 , (9.2)
, (9.2)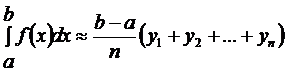 (9.2')
(9.2') Чем больше число n, тем меньше ошибка, совершаемая при вычислении на отрезке [a,b], то и для погрешности Rn формул прямоугольников справедлива следующая оценка:
Чем больше число n, тем меньше ошибка, совершаемая при вычислении на отрезке [a,b], то и для погрешности Rn формул прямоугольников справедлива следующая оценка: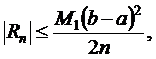 (9.3)
(9.3)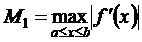 . Если задана точность вычислений ε, то из (3) можно найти число разбиений n отрезка [a,b], которое обеспечит эту точность
. Если задана точность вычислений ε, то из (3) можно найти число разбиений n отрезка [a,b], которое обеспечит эту точность
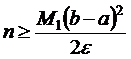 . (9.4)
. (9.4)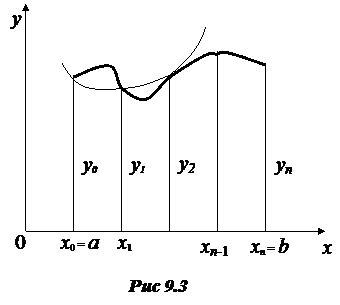 9.3. Формула трапеций.Естественно ожидать более точное значение интеграла (9.1), если данную кривую y = f(x) заменить не ступенчатой, как это было в формуле прямоугольников, а вписанной ломаной (рис. 9.3). Тогда площадь криволинейной трапеции aABb заменится суммой площадей прямолинейных трапеций, ограниченных сверху хордами АА1, А1А2, …, Аn-1B. Так как площади этих трапеций соответственно равны
9.3. Формула трапеций.Естественно ожидать более точное значение интеграла (9.1), если данную кривую y = f(x) заменить не ступенчатой, как это было в формуле прямоугольников, а вписанной ломаной (рис. 9.3). Тогда площадь криволинейной трапеции aABb заменится суммой площадей прямолинейных трапеций, ограниченных сверху хордами АА1, А1А2, …, Аn-1B. Так как площади этих трапеций соответственно равны

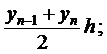
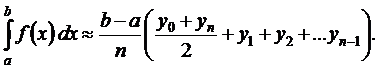 (9.5)
(9.5)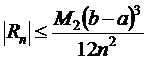 , (9.6)
, (9.6) 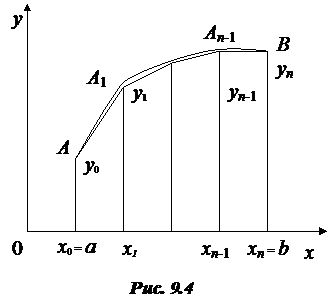 где
где 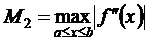 . Если задана точность вычислений ε, то из (9.6) можно найти число разбиений n отрезка [a,b], обеспечивающее эту точность
. Если задана точность вычислений ε, то из (9.6) можно найти число разбиений n отрезка [a,b], обеспечивающее эту точность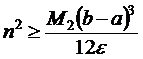 . (9.7)
. (9.7)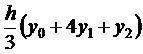 ,
,  , …,
, …,  ,
,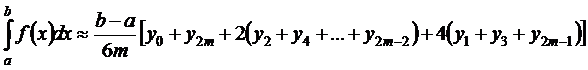 (9.8)
(9.8)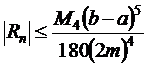 , (9.9)
, (9.9)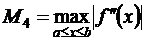 . Если задана точность вычислений ε, то из (9.9) можно найти число разбиений 2m = n отрезка [a,b], которое обеспечит эту точность
. Если задана точность вычислений ε, то из (9.9) можно найти число разбиений 2m = n отрезка [a,b], которое обеспечит эту точность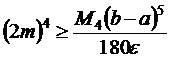 . (9.10)
. (9.10)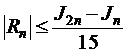 ,
, . За приближенное значение J интеграла (9.1), вычисленное по формуле парабол с поправкой Рунге, принимают
. За приближенное значение J интеграла (9.1), вычисленное по формуле парабол с поправкой Рунге, принимают 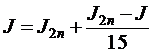 .
.