
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Первая интерполяционная формула Ньютона для равноотстоящих узлов интерполяции
Вычисление значений функции для значений аргумента, лежащих в начале таблицы, удобно проводить, пользуясь первой интерполяционной формулой Ньютона. Пусть функция f(x) задана значениями В силу единственности многочлена степени n, построенного по n + 1 значению функции f(x), многочлен Рn(x) является разновидностью записи интерполяционного многочлена и совпадает с Будем искать f(x) в виде
В этом выражении неизвестны коэффициенты а0, а1, а2, …, аn . Найдем а0, положив х = х0, тогда
Чтобы найти коэффициент а1, составим первую конечную разность для многочлена Рn(x) в точке х. Согласно определению конечной разности имеем
Проведя подстановку, получим
Вычислим первую конечную разность многочлена Рn(x) в точке х0. Здесь так же все члены, кроме первого, обратятся в ноль и, следовательно,
но
Чтобы определить коэффициент а2, составим конечную разность второго порядка:
После преобразований получим
Полагаем х = х0: тогда все члены, кроме первого, опять обратятся в ноль и
Вычисляя конечные разности более высоких порядков и полагая х = х0, получим общую формулу для получения коэффициентов
Подставив найденные значения коэффициентов аi в выражение (7.3), получим первую интерполяционную формулу Ньютона.
На практике часто используют формулу Ньютона в другом виде:
где  Если n = 1, то получим формулу линейного интерполирования
При n = 2 получим формулу параболического или квадратичного интерполирования
Эти формулы удобно применять в начале таблицы, когда q мало по абсолютной величине.
Вторая интерполяционная формула Ньютона
Для интерполирования в конце таблицы обычно применяют вторую интерполяционную формулу Ньютона. Пусть на [a,b] даны n + 1 различные значения аргумента х0, х1, …, хn ,, которым соответствуют следующие значения
а шаг интерполяции постоянен и равен h, т.е. Построим интерполяционный многочлен вида
В этом многочлене неизвестны коэффициенты а0, а1, а2, …, аn . Их надо подобрать так, чтобы были возможны равенства:
Для этого необходимо и достаточно, чтобы
Коэффициент а0 найдем, положив х = хn в равенстве (7.4)
откуда
Отсюда, полагая х = хn-1 имеем
Из выражения для второй конечной разности имеем а2
Полагая х = хn-2, получим
откуда
Подставляя найденные значения коэффициентов, получим :
Это и есть вторая интерполяционная формула Ньютона. Положим q = (x - xn)/h, тогда
Первая интерполяционная формула Ньютона используется для интерполирования в начале отрезка [a,b], а вторая – на конечном участке таблицы.
|
||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 286. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ;
; 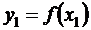 ; …;
; …; 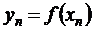 в равноотстоящих узлах интерполяции
в равноотстоящих узлах интерполяции 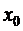 ,
, 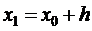 , …,
, …,  и требуется построить интерполяционный многочлен
и требуется построить интерполяционный многочлен  степени n такой, что
степени n такой, что 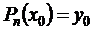 ;
; 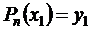 ; …;
; …;  .
. Лагранжа.
Лагранжа.
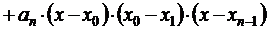 . (7.3)
. (7.3) .
. .
.
 ,
,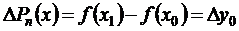 ;
; 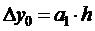 ;
;  .
.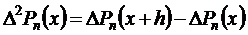 .
.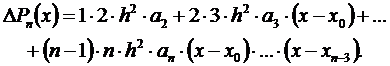
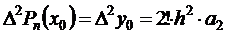 ,
,  .
. .
. (7.4)
(7.4)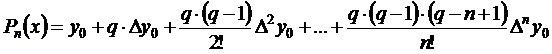 ,
, , h – шаг интерполирования и q – число шагов.
, h – шаг интерполирования и q – число шагов.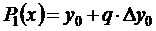 .
. .
. ;
;  ; …;
; …;  .
.
 ;
;  .
. .
.

 , следовательно
, следовательно .
.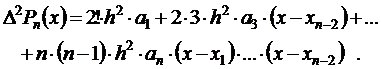
 ,
, ,
, 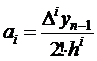 .
.
 ;
; 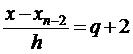 ;
; (7.5)
(7.5)