
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Приведение системы линейных уравнений к виду, удобному для итераций
Процессы последовательных приближений и метод Зейделя для линейных систем х = b + aC сходятся к единому решению, независимо от выбора начального вектора, если
или
Таким образом, для сходимости вышеуказанных итерационных процессов достаточно, чтобы значения элементов aij при i ¹ j были небольшими по абсолютной величине. Это равносильно тому, что если для линейной системы АХ = В модули диагональных коэффициентов каждого уравнения системы больше суммы модулей всех остальных коэффициентов (не считая свободных членов), то итерационные процессы для этой системы сходятся, т.е. мы имеем систему
Причем, если
ЛЕКЦИЯ 5. МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
При решении практических задач, часто приходится сталкиваться с решением уравнений. Всякое уравнение с одним неизвестным можно представить в виде
если обозначить левую часть за Совокупность нескольких уравнений с несколькими неизвестными называют системой уравнений.
Итерационные методы решения нелинейных уравнений
А). Метод простой итерации.
Представим уравнение 
б). Метод деления отрезка пополам (Дихотомии). Для 1. находим 2. вычисляем 3. если 4. Проверяем условие
Число итераций при использовании этого метода
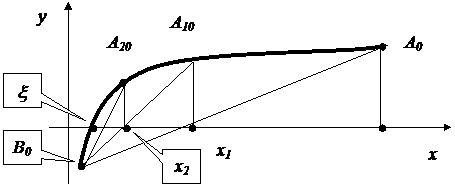
в). Метод Хорд. Пусть имеем уравнение Корень считается отделенным и находится на отрезке
Уравнение хорды проходящей через точку А0 и В (см. рис.5.1, рис.5.2)
Рис. 5.1
Рис. 5.2 имеет вид
Найдем х = х1, для которого y = 0
Если корень нас не устраивает, то мы находим
. . .
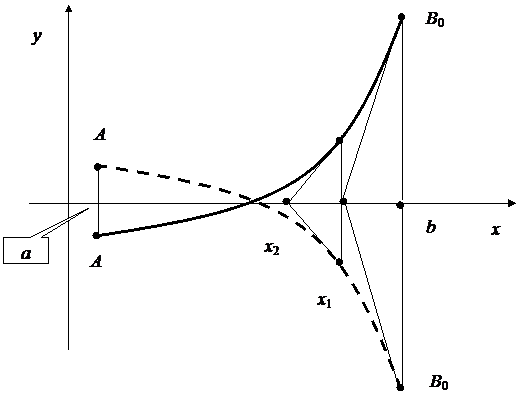
Рассмотрим случай, когда первая и вторая производные имеют разные знаки. (рис.5.3):
Рис. 5.3
. . .
Неподвижными концами отрезка является тот, для которого знак функции совпадает со знаком второй производной
Г). Метод Ньютона. Пусть корень уравнения f(x) = 0 отделен на отрезке [a, b], причем Геометрический смысл метода Ньютона в том, что дуга кривой y = f(x) заменяется касательной к этой кривой.
Первый случай (рис.5.4):
f(a) < 0 , f(b) > 0 , или f(a) > 0 , f(b) < 0 ,
Рис. 5.4
Проведем касательную к кривой y = f(x) в точке B0
Полагая y = 0 , x = x1 , получим
. . .
Второй случай (рис. 5.5):
f(a) < 0 , f(b) > 0 ,
или f(a) > 0 , f(b) < 0 ,
Рис. 5.5
Полагая y = 0 , х = х1, получим
При выборе начального приближения корня необходимо руководствоваться правилом: за исходную точку следует выбирать тот конец [a, b], в котором знак функции совпадает со знаком
д). Модифицированный метод Ньютона. Заключается в том, что вместо вычисления производной
Следовательно, итерационная формула имеет вид
Значение
Метод Рыбакова Можно рассматривать этот метод как модификацию метода Ньютона. При замене При Метод Рыбакова удобен для поиска всех корней уравнения f(x) = 0 на [a,b] . 1. Задаем начальные значения х = х0 = а . 2. Для каждой последовательной итерации ( n = 0, 1, 2, …) вычисляем
и проверяем условие xn < b, если оно выполняется, то, значит, найдены все корни, в противном случае проверяем выполнение условия 3. Задаем начальное приближение Метод наискорейшего спуска
Распространенным методом минимизации функций большого числа переменных является метод градиентного спуска. Последующее приближение получается из предыдущего смещением в направлении, противоположном градиенту функции F(x). Каждое следующее приближение ищется в виде
Приведенное описание не определяет алгоритм однозначно, т.к. ничего не сказано о выборе параметра В этом случае рассматриваемый метод называют методом наискорейшего градиентного спуска. Для функции
так как
и
Обозначим
Предположим, что
ЛЕКЦИЯ 6. ИНТЕРПОЛИРОВАНИЕ И ЭКСТРАПОЛИРОВАНИЕ
1. Математическая постановка задачи интерполирования. В экономике и технике, часто приходится сталкиватьcя с необходимостью вычисления значений функции у = f(х) в точках, отличных от значения аргумента, фиксированных в таблице. Подобные задачи практики формализуются как математические задачи интерполирования. Пусть на отрезке [a, b] задана функция у = f(х) своими n + 1 значениями Требуется найти аналитическое выражение табулированной функции F(х), совпадающее в узлах интерполяции со значениями заданной функции,
т.е.
Процесс вычисления значений функций в точках х, отличных от узлов интерполяции, называется интерполированием функции f(х). Если аргумент х находится за пределами отрезка интерполирования [x0 , xn], то задача определения значения функции в точке х называется экстраполированием. Задача становится однозначной, если в качестве интерполирующей функции f(х) для функции у = f(х), заданной своими n+1 значениями, выбрать многочлен Fn (x) степени не выше n, такой, что
Многочлен Fn(x) удовлетворяющий этим условиям, называют интерполяционным многочленом, а соответствующие формулы – интерполяционными. В случае, когда F(x) выбирается в классе степенных функций, интерполяция называется параболической.
При интерполировании возникает ряд задач:
1. Выбор наиболее удобного способа построения интерполяционной функции для каждого конкретного случая. 2. Оценка погрешности при замене f(x) интерполирующей функцией F(x) на отрезке [a, b]. 3. Оптимальный выбор узлов интерполяции для получения минимальной погрешности. |
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 288. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 .
.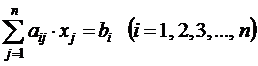 .
. то процессы последовательных приближений и Зейделя для данной системы сходятся. Применяя элементарные преобразования, линейную систему АХ = В можно заменить такой эквивалентной системой Х = р + aХ, для которой условия сходимости будут выполнены.
то процессы последовательных приближений и Зейделя для данной системы сходятся. Применяя элементарные преобразования, линейную систему АХ = В можно заменить такой эквивалентной системой Х = р + aХ, для которой условия сходимости будут выполнены. , где
, где  и
и  – заданные функции, определенные на некотором числовом множестве Х, называемом областью допустимых значений уравнения или
– заданные функции, определенные на некотором числовом множестве Х, называемом областью допустимых значений уравнения или
 , то получим уравнение
, то получим уравнение  .
. через
через  и многократным применением формулы
и многократным применением формулы  до тех пор, пока
до тех пор, пока  , где
, где  – заданная погрешность вычисления.
– заданная погрешность вычисления. :
: ;
; ;
; , задаем
, задаем  , иначе
, иначе  .
. : если оно выполняется, идем к п.1., если не выполняется, заканчиваем вычисление и считаем, что
: если оно выполняется, идем к п.1., если не выполняется, заканчиваем вычисление и считаем, что  приблизительно равен искомому решению исходного уравнения с заданной точностью
приблизительно равен искомому решению исходного уравнения с заданной точностью 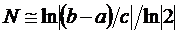 .
. , имеющая непрерывные
, имеющая непрерывные  и
и  .
.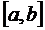 , т.е.
, т.е.

 .
. .
. ;
;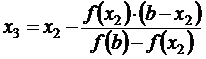 ;
; .
. ,
,  .
.
 ,
,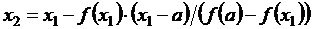 ,
,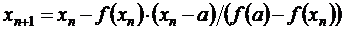 .
. .
.
 .
. ,
, ,
,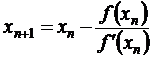 .
. .
.
 ,
, 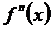 , т.е.
, т.е.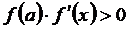 , a = x0 .
, a = x0 .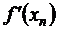 на каждом шаге итераций находится ее приближенное значение
на каждом шаге итераций находится ее приближенное значение ,
,  .
.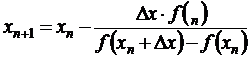 .
.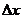 не обязательно должно быть постоянно. Равенство
не обязательно должно быть постоянно. Равенство 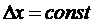 позволяет уменьшить число исходных данных при вводе.
позволяет уменьшить число исходных данных при вводе. , где
, где  – значение х на [a, b] , при котором производная
– значение х на [a, b] , при котором производная  сходимость не нарушается, но замедляется.
сходимость не нарушается, но замедляется.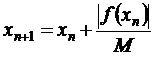
 . Если оно не выполняется, то повторяем цикл с пункта 2 и переходим к пункту 3.
. Если оно не выполняется, то повторяем цикл с пункта 2 и переходим к пункту 3.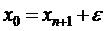 и снова идем на пункт 2.
и снова идем на пункт 2.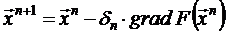 .
.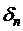 . Его можно определять из условия минимума величины
. Его можно определять из условия минимума величины 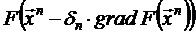 .
. , соответствующей системе линейных уравнений с матрицей
, соответствующей системе линейных уравнений с матрицей  , задача нахождения минимума решается в явном виде
, задача нахождения минимума решается в явном виде
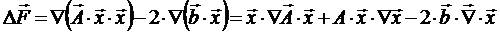
 .
.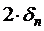 через
через 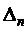 , т.е.
, т.е.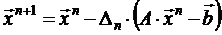 .
. . Учитывая, что
. Учитывая, что  , вычислим
, вычислим  :
: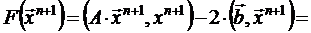


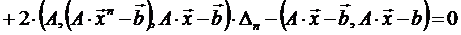 ,
, .
. ;
; 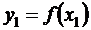 ; … ;
; … ; 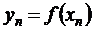 в точках x0, x1, …, xn , которые назовем узлами интерполяции.
в точках x0, x1, …, xn , которые назовем узлами интерполяции. ;
;  ; … ;
; … ;  .
. ;
;  ; … ;
; … ; 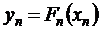 .
.