
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Понятие предела для векторов и матрицПусть дана последовательность векторов
с координатами
… , … , …, …
то вектор Аналогично, если имеется последовательность квадратных матриц
… ;
с элементами aij(1), … , aij(k); где i = 1, 2, …, n; j = 1, 2, …, n; то пределом последовательности матриц А(1), … , А(k) называется матрица с элементами
Сама же последовательности А(1), ... , А(k) называется сходящейся к А, т.е.
А(k) = А или
Из сказанного выше следует следующее утверждение: Если последовательность матриц А(1) , … , А(k) имеет пределом собственную матрицу А и вектора В(1) ,…, В(k) сходятся к В, то решения систем А(1)Х = В(1), … , А(k)Х = В(k) имеют предел, являющийся решением системы АХ = В, т.е. Х(k) = (А(k))-1 В(k) Метод простой итерации
Пусть дана система линейных уравнений:
В матричном виде:
Предполагая, что диагональные элементы aii ¹ 0 ,(j= 1, 2, …, n), выразим х1 через первое уравнение системы, х2 – через второе, и т.д.
… (3.5)
Обозначим
Эта система называется системой, приведенной к нормальному виду. 
Введя обозначения
Запишем систему (3.3) в матричной форме или
Решим систему (3.7) методом последовательного приближения, за нулевое приближение возьмем столбец свободных членов:
Любое приближение вычисляется по формуле X(k+1) = b + aХ(k). Если последовательность приближения X(0), X(1), …, X(k) имеет предел X = lim X(k) при k Условия сходимости итерационного процесса Пусть дана приведенная к нормальному виду система линейных уравнений X = b + aХ. Итерационный процесс и его сходимость зависят от величины элементов матрицы a следующим образом: если сумма модулей элементов строк или сумма модулей элементов столбцов меньше единицы, то процесс итераций для данной системы сходится к единственному решению независимо от выбора начального вектора. Следующее условие сходимости можно записать так:
Сходимость итерационного процесса связана с нормами матрицы a следующими соотношениями. Если выполняется одно из условий:
либо
либо
то процесс итераций линейной системы сходится к единственному решению.
|
||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 255. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ;
;  ; …
; …  (3.1)
(3.1) ; …
; …  . Если у каждой координаты существует предел
. Если у каждой координаты существует предел  , т.е.
, т.е.

 называется пределом последовательности векторов
называется пределом последовательности векторов  .
. ;
; ; (3.2)
; (3.2) .
. .
. .
. А-1В .
А-1В . . (3.3)
. (3.3)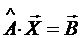 ,
, ;
;  . (3.4)
. (3.4)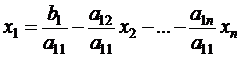 ;
; ;
; .
. ,
,  , где i = 1, …, n; j = 1, … , n , тогда
, где i = 1, …, n; j = 1, … , n , тогда (3.6)
(3.6) ,
,  .
.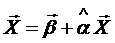
 . (3.7)
. (3.7) - нулевое приближение;
- нулевое приближение;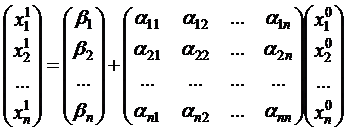 - 1-е приближение ;
- 1-е приближение ; - 2-е приближение .
- 2-е приближение .
 ,
,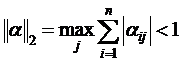 ,
, ,
,