
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Понятие о системе линейных уравнений
В общем виде система m линейных уравнений с n неизвестными записывается так:
Уравнения системы считаются пронумерованными: первое, второе, Коэффициент при неизвестном Кратко система (1.1) может быть записана:
Решением системы линейных уравнений называется любая совокупность чисел Совместная система линейных уравнений может иметь одно или несколько решений. Она называется определенной, если имеет одно решение, и неопределенной, если имеет больше одного решения. Две системы линейных уравнений с одним и тем же числом неизвестных называются эквивалентными, если они обе несовместны или совместны и имеют одни и те же решения. Пусть дана определенная система n линейных уравнений (1.1). Пользуясь матричными обозначениями её, можно заменить следующим:
где матрица системы
вектор-столбец неизвестных
вектор-столбец свободных членов
 Матричные уравнения Рассмотрим три вида матричных уравнений. 1. Уравнение вида
Пример: Находим обратную матрицу
2. Матричное уравнение вида:
Умножим обе части уравнения на
Пример:Решить матричное уравнение
Решение:
Матричное уравнение третьего вида: Для его решения умножим обе части уравнения слева на
Пример:Решить матричное уравнение
Решение:
Находим сначала
ЛЕКЦИЯ 2. ТОЧНЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (СЛАУ) СЛАУ допускают как точные, так и приближенные методы решения. К точным относятся метод Крамера, метод Гаусса и метод обратной матрицы. К приближенным методам относятся: метод простой итерации, метод последовательных приближений и метод Зейделя. Формулы Крамера для решения системы линейных уравнений
Пусть дана система линейных уравнений (для простоты возьмем систему 4-го порядка)
Введем специальные обозначения, где D – определитель системы
Если D ¹ 0, то система является определенной, т.е. имеет единственное решение в виде соотношений, которые и называются формулами Крамера
Решение системы линейных уравнений методом последовательного исключения неизвестных (метод Гаусса)
Элементарными преобразованиями называются следующие 3 типа преобразований: 1. Перестановка двух уравнений системы. 2. Умножение обеих частей уравнений системы на любое число неравное нулю. 3. Прибавление (вычитание) к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число, отличное от нуля. Пусть дана система
Будем исключать неизвестное x1 из всех уравнений системы (2.4), кроме первого. Назовем x1 – ведущим неизвестным, а коэффициент a11 – ведущим коэффициентом. Разделив первое уравнение на a11 (это возможно если a11 ¹ 0), получим:
Обозначим
и вообще
тогда
или
Дальнейшее решение системы уравнений (2.4) методом Гаусса представляет собой ряд последовательных шагов: 1. Для исключения неизвестного вычтем из второго уравнения системы (2.4) уравнение (2.5), умноженное на a21 :
−
___________________________________________________________
Обозначим
Перепишем полученное уравнение в виде
2. Из третьего уравнения системы (2.4) вычтем уравнение (2.5) умноженное на
– ________________________________________________________
Обозначим
Перепишем полученное уравнение в виде
3. Из четвертого уравнения системы (2.4) вычитаем уравнение (2.5), умноженное на
где
В результате элементарных преобразований имеем систему 3-х уравнений с тремя неизвестными, эквивалентную системе (2.4) :
где коэффициент
Разделив далее коэффициент первого уравнения системы (2.4) на ведущий коэффициент
обозначим
или
Исключая теперь
где Разделив коэффициенты первого уравнения системы (2.7) на ведущий коэффициент и ведущий коэффициент
где
Исключив теперь х3 , аналогичным путем из системы (2.8), находим:
где
отсюда
Остальные неизвестные системы последовательно определяются из уравнений (2.5, 2.8, 2.9, 2.10):
Таким образом, процесс решения системы линейных уравнений по методу Гаусса сводится к построению эквивалентной системы уравнений (2.5, 2.8, 2.9, 2.10, …). Метод Гаусса применим при условии, что все ведущие коэффициенты отличны от нуля. Для удовлетворения данных условий вычисления проводятся по схеме единственного деления.
ЛЕКЦИЯ 3. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ Приближенные методы решения систем линейных уравнений позволяют получать значения корней системы с заданной точностью в виде предела последовательности некоторых векторов. Процесс повторения такой последовательности называется итерационным (повторяющимся). Эффективность применения приближенных методов зависит от удачного выбора начального вектора и быстроты сходимости процесса. Мы рассмотрим два метода - метод последовательных приближений и метод Зейделя. |
||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 295. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1.1)
(1.1)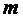 - е,
- е, 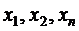 – неизвестные,
– неизвестные, 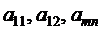 – коэффициенты при неизвестных.
– коэффициенты при неизвестных.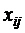 в i – уравнении обозначается через
в i – уравнении обозначается через 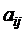 , j – номер неизвестного.
, j – номер неизвестного.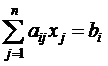 , (i = 1, 2, …, m). (1.2)
, (i = 1, 2, …, m). (1.2)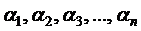 , которая, будучи подставленной на место неизвестных
, которая, будучи подставленной на место неизвестных  в уравнение данной системы, обращает все эти уравнения в тождества. Система (1.1) – совместная, если она имеет решение. Если система не имеет решений, то она называется несовместной или противоречивой.
в уравнение данной системы, обращает все эти уравнения в тождества. Система (1.1) – совместная, если она имеет решение. Если система не имеет решений, то она называется несовместной или противоречивой.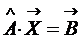 , (1.3)
, (1.3)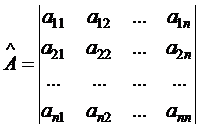 ; (1.4)
; (1.4)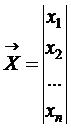 ; (1.5)
; (1.5) . (1.6)
. (1.6)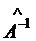 слева:
слева: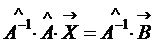 , где
, где 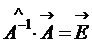 . (1.7)
. (1.7)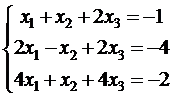 или
или 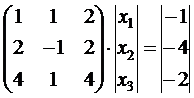 .
.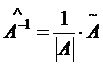 .
. 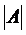 - детерминант матрицы A.
- детерминант матрицы A. - алгебраическое дополнение к матрице A.
- алгебраическое дополнение к матрице A.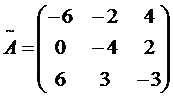 ;
; 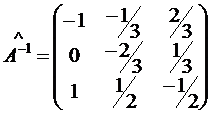 .
.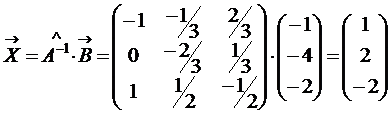
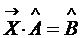 (1.8)
(1.8)
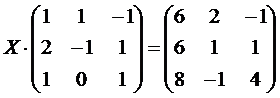 .
. ~
~ 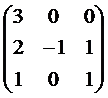 ;
; 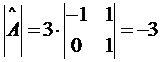 ;
;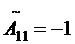 ;
; 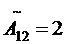 ;
; 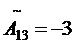 ;
;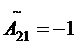 ;
; 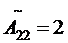 ;
; 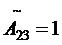 ;
;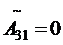 ;
;  ;
; 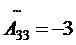 ;
;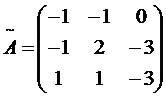 ;
; 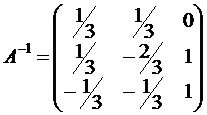 ;
;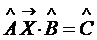 . (1.9)
. (1.9)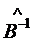 , тогда получим
, тогда получим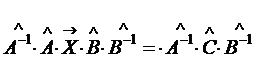 ;
;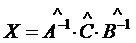 .
. .
.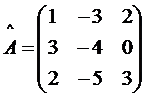 ;
; 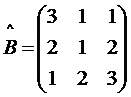 ;
; 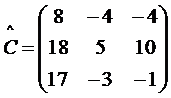 ;
; ;
; 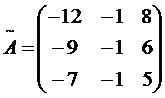 ;
; 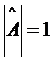 ;
;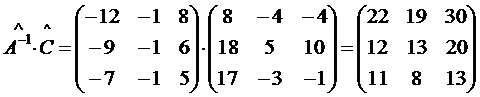 .
.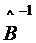 , а затем и искомое решение матричного уравнения
, а затем и искомое решение матричного уравнения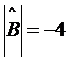 ;
; 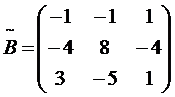 ;
; 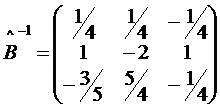 ;
;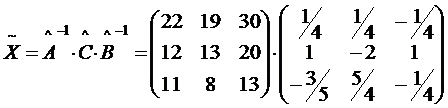 .
.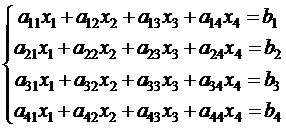 (2.1)
(2.1)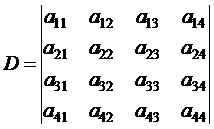 ;
; 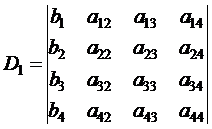 ;
;  ;
;  ; (2.2)
; (2.2)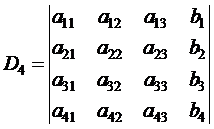 .
.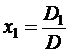 ;
; 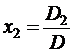 ;
; 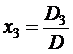 ;
;  , (2.3)
, (2.3)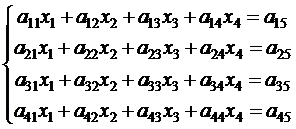 (2.4)
(2.4)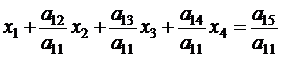 .
.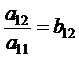 ;
; 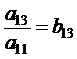 ;
; 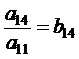 ;
; 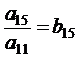 ;
;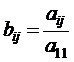 , (j > 0) ,
, (j > 0) ,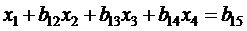
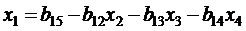 . (2.5)
. (2.5)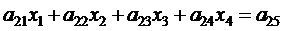
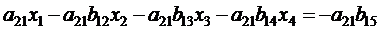
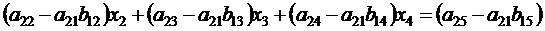

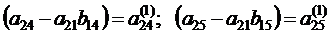 .
.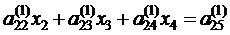 .
.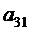
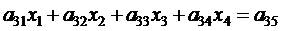
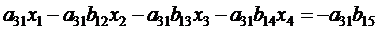
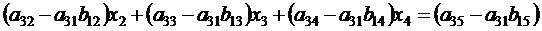
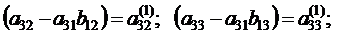
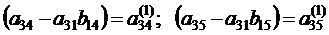 .
.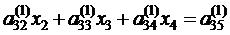 .
. . Применив аналогичные преобразования, получим следующее уравнение:
. Применив аналогичные преобразования, получим следующее уравнение: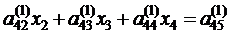 ,
,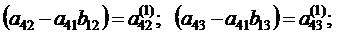
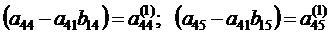 .
.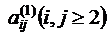 вычисляется по формуле
вычисляется по формуле 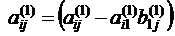 .
.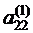 , получим первое уравнение системы в виде :
, получим первое уравнение системы в виде :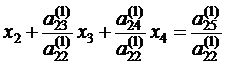 ,
,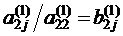 , где j > 2 , тогда первое уравнение системы (2.4) примет вид :
, где j > 2 , тогда первое уравнение системы (2.4) примет вид :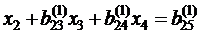
 .
.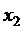 из всех уравнений системы (2.4), кроме первого, мы получим систему двух уравнений с двумя неизвестными:
из всех уравнений системы (2.4), кроме первого, мы получим систему двух уравнений с двумя неизвестными: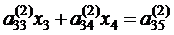
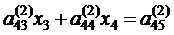 , (2.7)
, (2.7)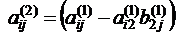 ,
, 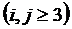 .
.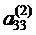 получим
получим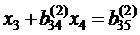 , (2.8)
, (2.8)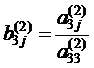 , j > 3, то есть
, j > 3, то есть  .
.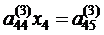 , (2.9)
, (2.9)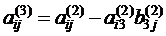 ,
, 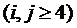 ;
; . (2.10)
. (2.10)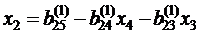 ;
;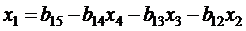 .
.