
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ПРЕДРАСЧЕТ ТОЧНОСТИ ИЗМЕРЕНИЙСтр 1 из 3Следующая ⇒ Примеры задач Сделай сам(а)
31u2 - u1 C= Р = С(u2 - u1) где С – цена деления планиметра.
Средняя квадратическая погрешность функции z=f(x,y,….t) измеренных величин (косвенных измерений) равна
32n =
Ф-ла из 32) Так как точность теодолита m=30″, а средняя квадратическая погрешность Mβ○ не должна превышать ..″ то, подставляя в исходные данные, получим n=9 приемов.
36находят арифметическую середину из результатов измерений, как Lср = Σ Li/n; вычисляют уклонения от арифметической середины υ = Li - Lср. ; вычисляют среднюю квадратическую погрешность по формуле Бесселя m= Σ υ
37D1=l1, D2=l2……. Lср = [pili]/ [p]. [p]=p1+p2+p3….. 38Решение данной задачи можно показать на предыдущем примере, если предположить, что точное значение измеряемой величины Х отсутствует. Порядок вычислений: находят арифметическую середину из результатов измерений, как Lср = Σ Li/n; вычисляют уклонения от арифметической середины υ = Li - Lср. ; вычисляют среднюю квадратическую погрешность по формуле Бесселя m= Σ υ2/ (n-1); определяют среднюю квадратическую погрешность самой погрешности по формуле m m = m 2 n; находят предельную погрешность как mпред =3 m; вычисляют относительную среднюю квадратическую погрешность mотн = m / Lср; вычисляют среднюю квадратическую погрешность арифметической средины MLср = m /√ n; записывают окончательный результат как Lср ±3 MLср.
Примеры задач:Примеры задач (1–5) для самостоятельного решения Пример 1.В прямоугольнике измерены длины сторон: а = 32,62 м, b = 52,37 м. Средние квадратичные ошибки измерения сторон равны: ma = 0,01 м, mb = 0,02 м. Требуется определить среднюю квадратическую ошибку определения площади прямоугольника. Площадь S = ab; среднюю квадратическую ошибку определения площади получим по рассмотренной выше методике: 
Пример 2.Требуется определить среднюю квадратическую ошибку mh определения превышения в тригонометрическом нивелировании, полученного по формуле: h = d tg v, где d = 144,0 м, v = +2º30´, md = 0,5 м, mv = 1´; тогда h = 6,27 м. Формула для вычисления mh: где
Пример 3. В треугольнике измерены два горизонтальных угла со средними квадратическими ошибками Пример 4.Требуется определить среднюю квадратическую ошибку определения приращения координат ∆x = l∙cos α, если l = 489,98 м; ml = 0,11 м; α = 144º30´; mα = 1´. Вычисления выполняют по формуле:
Пример 5. Найти среднюю квадратическую ошибку длины линии D, измеренную стальной двадцатиметровой лентой, если средняя квадратическая ошибка одного обложения ленты
Считаем, что отложение двадцатиметровых отрезков лентой равноточное, тогда mD = ml∙ Задание для индивидуального решения студентами пяти вышеприведенных примеров заключается в том, что длины сторон или их горизонтальное проложение выбираются студентами по варианту, для чего к длинам линий в примерах прибавляется число целых метров, соответствующих номеру варианта. Номер варианта у каждого студента соответствует его порядковому номеру в журнале группы. Например, студенту, имеющему шестой номер в журнале, соответствует шестой вариант и для первого примера ему следует взять следующие длины сторон в прямоугольнике: а = 32,62 + 6 = 38,62 м; b = 52,37 + 6 = 58,37 м. Все остальные исходные данные, помимо длин линий, берутся из приведенных примеров. ПРЕДРАСЧЕТ ТОЧНОСТИ ИЗМЕРЕНИЙ В практике геодезических работ, особенно на стадии составления проектов, возникает необходимость рассчитать точность предстоящих измерений, пользуясь теорией ошибок. При этих расчетах по известному виду функции требуется рассчитать точность измерения каждого аргумента. В таких случаях применяют принцип равных влияний, суть которого состоит в требовании равенства слагаемых в формуле средней квадратической ошибки функции общего вида. Пример. Превышение получено по формуле h = Применим принцип равного влияния, то есть потребуем, чтобы влияние ошибок измерений расстояния l и угла v было одинаковым: подставив в формулы значения величин, получим:
Как видно из полученных результатов, необходимая точность получения превышения достигается теодолитом 2Т-30 с использованием нитяного дальномера или кипрегелем. Задача для самостоятельного решения студентами по вариантам. Площадь прямоугольника со сторонами а = 200 м, b = 160 м, требуется определить со средней квадратической ошибкой m, не превышающей 4 м2. Следует рассчитать, с какой точностью необходимо измерять стороны прямоугольника, чтобы обеспечить заданную точность определения площади. S = a b,
Из полученных результатов можно сделать вывод о том, что для обеспечения точности определения площади с mS = 4 м2 необходимо измерять длины линий с точностью ≈ ±3 см. Для решения задачи самостоятельно каждый студент прибавляет к длинам а и b номер своего варианта, соответствующий порядковому номеру в журнале группы. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 381. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
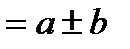
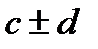
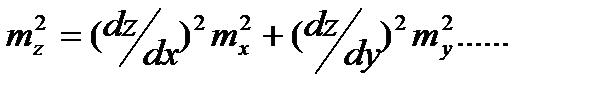

 =
= 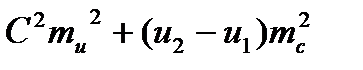
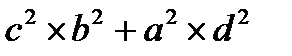
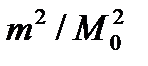
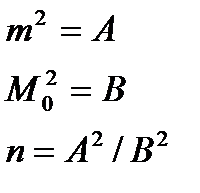
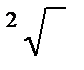 (n-1) ;
(n-1) ; , или
, или  м2.
м2. ,
, =3438´;
=3438´; м ≈ 5 см.
м ≈ 5 см. ,
,  . Требуется определить среднюю квадратическую ошибку
. Требуется определить среднюю квадратическую ошибку  третьего угла, полученного из двух измеренных значений. Определение выполняют по формуле:
третьего угла, полученного из двух измеренных значений. Определение выполняют по формуле: 
 м.
м. = ±1,2 см; D = 180 м.
= ±1,2 см; D = 180 м. , (14)
, (14) .
. см.
см. . Требуется рассчитать, с какой точностью должны быть измерены расстояние (l = 120 м) и угол наклона (v = 4º00´), если h необходимо получить со средней квадратической ошибкой mh = ±4,0 см. Рассматривая формулу превышения как функцию общего вида, находим:
. Требуется рассчитать, с какой точностью должны быть измерены расстояние (l = 120 м) и угол наклона (v = 4º00´), если h необходимо получить со средней квадратической ошибкой mh = ±4,0 см. Рассматривая формулу превышения как функцию общего вида, находим:  . (15)
. (15) , откуда
, откуда  и
и  ;
; см или
см или  ;
; .
. или, применив принцип равных влияний, получим:
или, применив принцип равных влияний, получим: ;
;



 м.
м.