Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ ФУНКЦИЙЗАДАЧИ И РЕШЕНИЯ Задача 1.Найти сумму элементов 3-го столбца матрицы В,
Решение. При умножении матрицы размера
Аналогично, находим
Тогда сумма этих элементов
Задача 2.Найти
Решение. Вычислим определитель матрицы А:
Так как
Здесь
Найдем алгебраические дополнения элементов
где Получим
Итак,
Наконец, находим обратную матрицу
Задача 3. Найти сумму элементов 3-й строки матрицы
Решение. Вычислим определитель матрицы А:
Запишем транспонированную матрицу
Так как надо найти сумму элементов 3-й строки матрицы
Тогда элементы 3-й строки матрицы
Их сумма равна Задача 4. Дана система уравнений
Найти Решение. Согласно формулам Крамера решение системы определяется соотношениями 
Найдем
Чтобы найти
Находим z:
Задача 5. Решить систему уравнений, приняв в качестве базисных переменных y и z:
Решение. Решаем систему методом Гаусса. Запишем расширенную матрицу системы – матрицу из коэффициентов при неизвестных и свободных членов
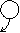   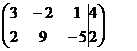 ~ ~
Среди коэффициентов при неизвестных есть 1, ей соответствует переменная z. Назовем z базисной переменной. Исключим базисную переменную z из 2-го уравнения, для чего умножим 1-е уравнение на 5 и сложим со 2-м. Получим эквивалентную исходной систему уравнений с матрицей
Умножим 2-е уравнение на (-1):
  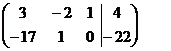 ~ ~
Считая новой базисной переменной у, исключим её из 1-го уравнения. Для этого умножим 2-е уравнение на 2 и сложим с 1-м:
В каждом уравнении выбирают одну базисную переменную, оставшиеся переменные называют свободными (в данном случае это х). Запишем систему уравнений, соответствующую последней матрице
Выразив базисные переменные (у и z) через свободную (х), получим общее решение системы уравнений
Задача 6. Решение. Воспользуемся формулой
где Вычислим
Найдем модули векторов
Тогда
Задача 7.Вектор Решение. Так как вектор
С другой стороны,
Итак,
Задача 8. Найти
Решение. Проекция вектора
Найдем координаты вектора
Вычислим скалярное произведение векторов
и модуль вектора
Тогда
Задача 9. Известно, что Решение. Согласно определению векторного произведения
Тогда Подставив исходные данные, получим
Задача 10. Найти площадь треугольника с вершинами в точках Решение. Площадь треугольника, построенного на векторах
где
Примем
Найдем векторное произведение этих векторов
Тогда
Следовательно,
Задача 11.Определить Решение. Условие компланарности трех векторов имеет вид
где
Подставляя исходные данные, получим
откуда
Задача 12.Найти объём треугольной пирамиды с вершинами в точках Решение. Найдем координаты векторов
Вычислим смешанное произведение этих векторов
Объём треугольной пирамиды, построенной на векторах
Задача 13.Записать уравнение прямой, проходящей через точки Решение. Уравнение прямой, проходящей через две точки
Подставляя координаты точек А и В, получим
Задача 14.Написать уравнение прямой, проходящей через точку Решение. Так как прямая перпендикулярна плоскости, то в качестве направляющего вектора Тогда
Поскольку уравнение прямой, проходящей через точку
получим
Задача 15.Определить, при каких
Решение. Условие параллельности двух прямых – это условие коллинеарности их направляющих векторов
Подставляя координаты
Тогда
Задача 16.Составить уравнение плоскости, проходящей через точки Решение. Уравнение плоскости, проходящей через три точки
Вычисляем определитель
Получаем уравнение плоскости
Задача 17.Определить, при каком А прямая Решение. Условие параллельности прямой и плоскости – это условие ортогональности направляющего вектора
Применяя эту формулу для
Задача 18.Найти точку пересечения прямой
и плоскости Решение. Перейдем к параметрическим уравнениям прямой
Найдем значение t, соответствующее точке пересечения прямой и плоскости, для чего подставим полученные выражения в уравнение плоскости
Подставляя
Задача 19.Найти канонические уравнения прямой пересечения двух плоскостей
Решение. Уравнение прямой пересечения двух плоскостей получим, решив совместно систему уравнений методом Гаусса.
Возьмем у в качестве базисной переменной и исключим у из 2-го уравнения, для чего умножим 1-е уравнение на (-3) и сложим со 2-м уравнением. Получим
Разделим 2-е уравнение на (-4):
  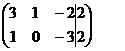 ~ ~
Возьмем в качестве следующей базисной переменной х и исключим её из первого уравнения, умножив 2-е уравнение на (-3) и сложив с 1-м уравнением:
Запишем получившуюся систему уравнений:
Выразим базисные переменные х и у через свободную переменную z:
Обозначив
Исключив параметр
Задача 20.Составить уравнение плоскости, проходящей через точки Решение. Пусть
Так как то
Тогда уравнение искомой плоскости будет иметь вид
Задача 21.Составить уравнение плоскости, проходящей через прямые
Решение. Пусть
Задача 22.Найти собственные значения матрицы
Решение. Собственные значения
Задача 23.Найти координаты вектора Решение. При разложении вектора
Здесь Запишем это равенство в координатной форме
Оно равносильно системе уравнений
Решим систему, например, по формулам Крамера:
Тогда
Значит, координаты вектора
Задача 24.Определить вид и расположение кривой
Решение. Чтобы определить, какая кривая представлена данным уравнением, необходимо привести уравнение к каноническому виду. Для этого выделим полные квадраты при переменных x и y:
Полученное уравнение соответствует уравнению эллипса
с полуосями Задача 25. Составить уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, если её действительная полуось равна 3, а расстояние между фокусами Решение. Уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, имеет вид
Действительная полуось этой гиперболы
Так как Итак, искомое уравнение гиперболы
Задача 26. Вычислить Решение. Числитель и знаменатель дроби неограниченно возрастают при
Так как при
Задача 27. Вычислить Решение. При Задача 28. Вычислить Решение. В данном случае имеет место неопределенность вида
Задача 29. Вычислить Решение. При Так как при Теперь можно воспользоваться формулой
где Тогда
Задача 30. Вычислить Решение. Это неопределенность
В данном случае
Задача 31.Вычислить Решение. При Преобразуем выражение, используя свойства логарифмов:
Так как
Тогда
Так как
при Тогда Задача 32. Решение. Применяя формулы дифференцирования произведения и частного
получим
Подставим в производную
Задача 33. Решение. Применим правило дифференцирования сложной функции: если
В данном случае
поэтому
Тогда
Задача 34. Решение. Это показательно-степенная функция. Преобразуем её в показательную, используя свойства логарифмов:
Получившуюся функцию дифференцируем как сложную
Тогда
Задача 35. Вычислить Решение. Преобразуем данную функцию
Вычислим частную производную
Найдем
Подставим вместо х и у координаты точки
Тогда
Задача 36.Найти Решение. Функция
Так как
то
Задача 37. Решение. Согласно формуле дифференцирования сложной функции
Так как
то
Тогда
Задача 38.Найти Решение. Функция В этом случае можно воспользоваться формулой
Так как
то
Задача 39. Найти асимптоты кривой Решение. Асимптоты бывают вертикальные и наклонные. Прямая
Прямая
Так как знаменатель дроби Ищем наклонные асимптоты:
Тогда наклонная асимптота имеет вид Задача 40. Найти интервалы убывания функции
Решение. Функция
Определим знаки производной и промежутки монотонности функции:
Итак, функция убывает на интервале Задача 41.Найти интервалы выпуклости функции
Решение. Функция
Определим знаки
Итак, функция выпукла при
Найти точки разрыва и установить их характер. Решение. Функция
Последнее равенство означает, что
Точки, в которых не выполняется, хотя бы одно из перечисленных условий, называются точками разрыва функции Если В том случае, когда - устранимый, если - со скачком, если (величина скачка Рассмотрим заданную функцию при Вычислим односторонние пределы:
Итак, Если Вычислим односторонние пределы:
Так как В качестве точки, похожей на разрыв, следует рассмотреть В этой точке функция определена:
Найдем односторонние пределы:
Итак, для точки
Таким образом, заданная функция имеет 3 точки разрыва: устранимый разрыв I рода при
Задача 43.Найти максимальную скорость возрастания функции Решение. Известно, что максимальная скорость возрастания функции
Найдем градиент функции
Вычислим градиент в точке М (2;1):
Тогда максимальная скорость возрастания функции
Задача 44.Найти производную функции Решение. Производная функции
где
Найдем частные производные функции
Их значения в точке М(1;-3) равны
Вычислим направляющие косинусы вектора
Тогда производная функции по направлению равна |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 201. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
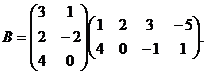
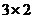 на матрицу размера
на матрицу размера 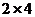 получится матрица размера
получится матрица размера 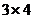 (3 строки и 4 столбца). Таким образом, в 3-м столбце будет 3 элемента:
(3 строки и 4 столбца). Таким образом, в 3-м столбце будет 3 элемента:  . Далее умножение матриц осуществляется по правилу: элемент
. Далее умножение матриц осуществляется по правилу: элемент  матрицы
матрицы  , стоящий в i-той строке и к-том столбце, равен сумме произведений соответствующих элементов i-той строки матрицы А и к-того столбца матрицы С. Таким образом, чтобы найти
, стоящий в i-той строке и к-том столбце, равен сумме произведений соответствующих элементов i-той строки матрицы А и к-того столбца матрицы С. Таким образом, чтобы найти 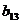 , нужно 1-ю строку матрицы А умножить на 3-й столбец матрицы С:
, нужно 1-ю строку матрицы А умножить на 3-й столбец матрицы С: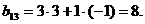
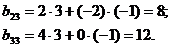
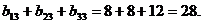
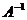 , если
, если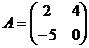 .
.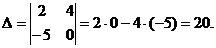
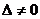 , то
, то 
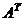 - транспонированная матрица, которая получается из матрицы А, если поменять местами строки и столбцы:
- транспонированная матрица, которая получается из матрицы А, если поменять местами строки и столбцы: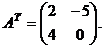
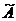 - союзная матрица, состоящая из алгебраических дополнений элементов
- союзная матрица, состоящая из алгебраических дополнений элементов 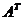 по формуле
по формуле
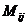 - минор - определитель, остающийся после вычеркивания строки i и столбца j матрицы
- минор - определитель, остающийся после вычеркивания строки i и столбца j матрицы 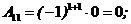

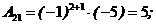
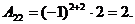
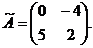
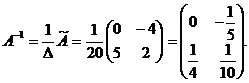
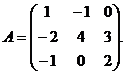
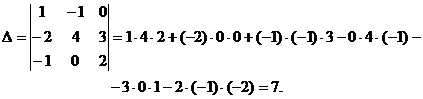
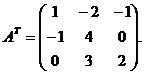
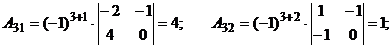
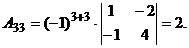
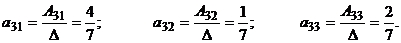
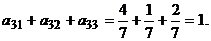
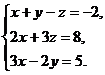
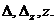
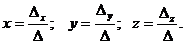
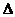 - определитель из коэффициентов, стоящих перед неизвестными
- определитель из коэффициентов, стоящих перед неизвестными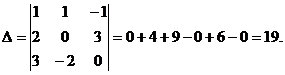
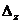 , необходимо элементы 3-го столбца определителя
, необходимо элементы 3-го столбца определителя 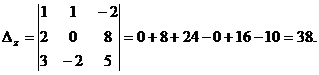
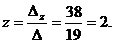
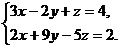
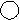
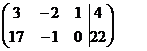 ~
~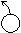


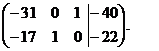
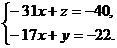
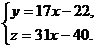
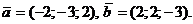 Найти
Найти 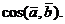
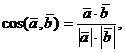
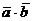 - скалярное произведение векторов
- скалярное произведение векторов 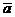 и
и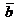 .
.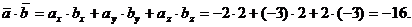
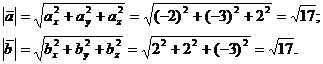
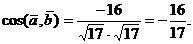
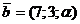 ортогонален вектору
ортогонален вектору 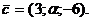 Найти
Найти 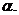
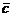 ,то
,то 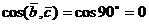 , и значит, скалярное произведение этих векторов тоже равно нулю:
, и значит, скалярное произведение этих векторов тоже равно нулю: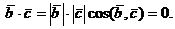

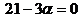 и
и 
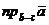 ,если
,если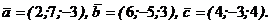
 определяется по формуле
определяется по формуле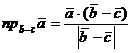 .
.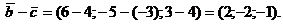
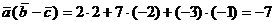
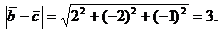
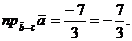
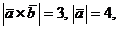 а угол между
а угол между 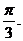 Найти
Найти 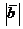 .
.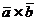 имеет место формула
имеет место формула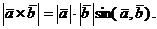
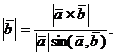
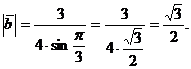
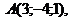
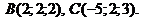

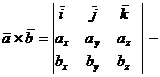 векторное произведение векторов
векторное произведение векторов  ,
, 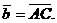 Вычислим координаты векторов
Вычислим координаты векторов 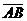 и
и  :
:
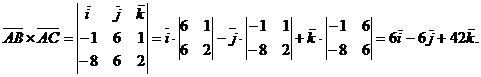
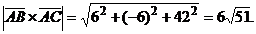
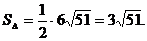
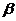 , при котором компланарны векторы
, при котором компланарны векторы 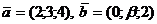 и
и 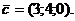
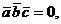
 -смешанное произведение векторов
-смешанное произведение векторов 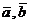 и
и 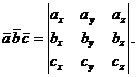
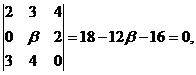

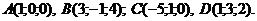
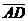 , на которых построена пирамида:
, на которых построена пирамида: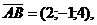
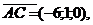
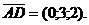
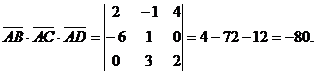
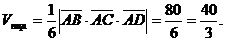
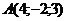
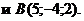
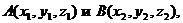 имеет вид
имеет вид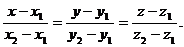
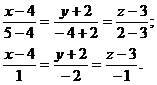
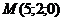 , перпендикулярно плоскости
, перпендикулярно плоскости 
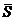 прямой можно взять нормальный вектор
прямой можно взять нормальный вектор 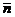 плоскости.
плоскости.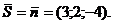
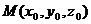 с направляющим вектором
с направляющим вектором 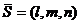 , имеет вид
, имеет вид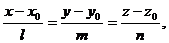

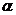 и
и 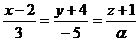 и
и 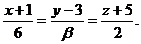
 и
и 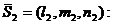
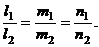
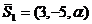 и
и 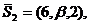 получим
получим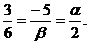
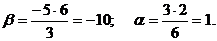
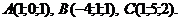
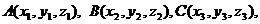 имеет вид
имеет вид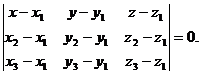
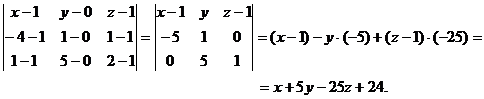
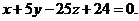
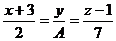 параллельна плоскости
параллельна плоскости 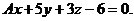
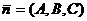 плоскости:
плоскости:
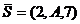 и
и 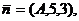 получим
получим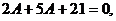 т. е.
т. е. 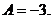
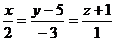

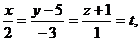 откуда
откуда 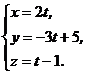
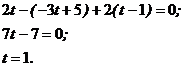
 в параметрические уравнения прямой, найдем координаты точки пересечения прямой и плоскости
в параметрические уравнения прямой, найдем координаты точки пересечения прямой и плоскости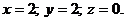
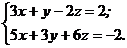


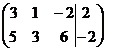 ~
~
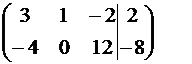 ~
~
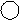
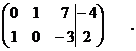
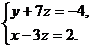

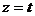 , получим параметрические уравнения прямой
, получим параметрические уравнения прямой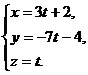
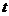 , перейдем к каноническим уравнениям прямой
, перейдем к каноническим уравнениям прямой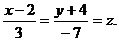
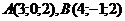 параллельно вектору
параллельно вектору 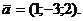
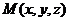 - произвольная точка искомой плоскости. Тогда векторы
- произвольная точка искомой плоскости. Тогда векторы 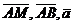 - компланарны. Запишем условие компланарности трех векторов:
- компланарны. Запишем условие компланарности трех векторов: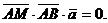
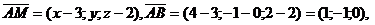
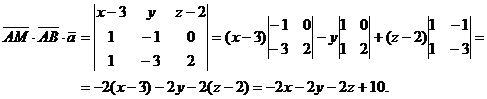
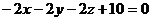 или
или 
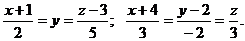
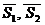 - направляющие векторы прямых,
- направляющие векторы прямых, 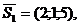
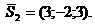 Уравнение искомой плоскости получим, записав условие компланарности векторов
Уравнение искомой плоскости получим, записав условие компланарности векторов 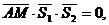 где А – точка, лежащая в искомой плоскости (в качестве такой точки можно взять любую точку, принадлежащую любой из двух прямых, например, А(-1; 0; 3). Так как
где А – точка, лежащая в искомой плоскости (в качестве такой точки можно взять любую точку, принадлежащую любой из двух прямых, например, А(-1; 0; 3). Так как 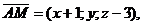 получим
получим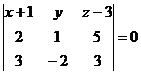 или
или 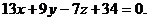

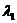 и
и 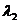 матрицы А находим, решая характеристическое уравнение:
матрицы А находим, решая характеристическое уравнение:
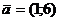 в базисе
в базисе 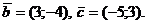
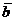 ,
, 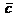 , необходимо представить
, необходимо представить 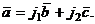
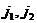 - есть координаты вектора
- есть координаты вектора 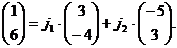
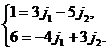
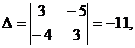
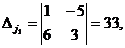
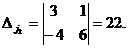
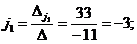

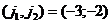 .
.
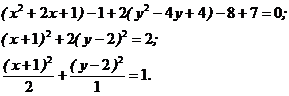
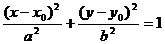
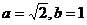 и центром в точке
и центром в точке 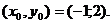
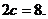
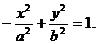
 . Найдем а из соотношения
. Найдем а из соотношения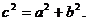
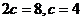 и
и 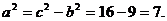
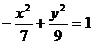 или
или 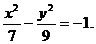
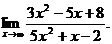
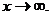 В этом случае говорят, что имеет место неопределенность вида
В этом случае говорят, что имеет место неопределенность вида 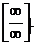 Разделим числитель и знаменатель дроби на старшую степень переменной, т. е. на
Разделим числитель и знаменатель дроби на старшую степень переменной, т. е. на 
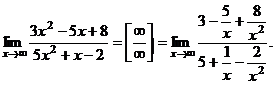
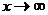 каждая из дробей
каждая из дробей 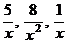 ,
,  стремится к нулю, получим
стремится к нулю, получим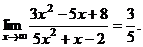
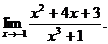
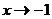 числитель и знаменатель дроби стремятся к 0. Это неопределенность вида
числитель и знаменатель дроби стремятся к 0. Это неопределенность вида 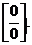 Разложим на множители числитель и знаменатель дроби и выполним сокращение
Разложим на множители числитель и знаменатель дроби и выполним сокращение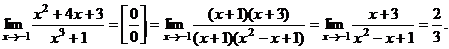
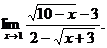
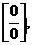 так как при
так как при 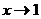 числитель и знаменатель стремятся к нулю. Умножим числитель и знаменатель дроби на выражения, сопряженные к ним, т. е. на
числитель и знаменатель стремятся к нулю. Умножим числитель и знаменатель дроби на выражения, сопряженные к ним, т. е. на 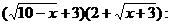
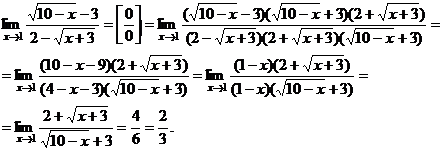
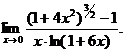
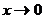 числитель и знаменатель – бесконечно малые величины. Заменим их эквивалентными бесконечно малыми.
числитель и знаменатель – бесконечно малые величины. Заменим их эквивалентными бесконечно малыми. 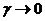
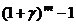 ~
~  ,
, 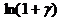 ~
~ 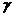 , то
, то  ~
~ 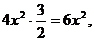
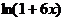 ~6x.
~6x.
 - бесконечно малые, причем
- бесконечно малые, причем 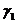 ,
, 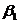 .
.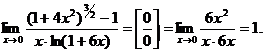
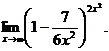
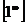 . Раскрываем её с помощью второго замечательного предела
. Раскрываем её с помощью второго замечательного предела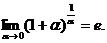
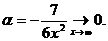 Поэтому
Поэтому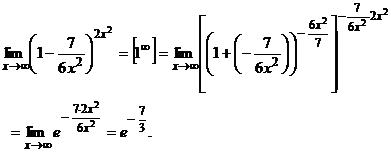
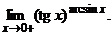
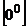 .
.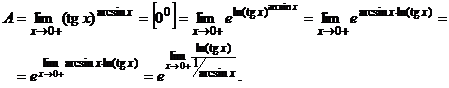
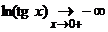 ,
, 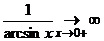 , имеем неопределенность
, имеем неопределенность 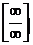 , которую раскрываем по правилу Лопиталя:
, которую раскрываем по правилу Лопиталя: 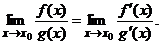
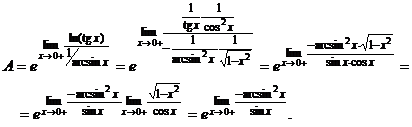
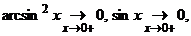 получили неопределенность
получили неопределенность 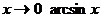 ~х,
~х, 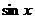 ~х.
~х.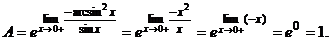
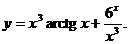 Найти
Найти 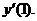
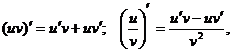
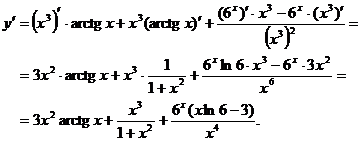
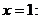
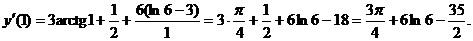 Замечание. Здесь и далее используются формулы дифференцирования, приведенные в конце работы.
Замечание. Здесь и далее используются формулы дифференцирования, приведенные в конце работы. . Найти
. Найти 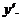
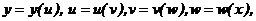 то
то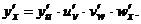
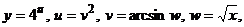
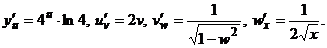
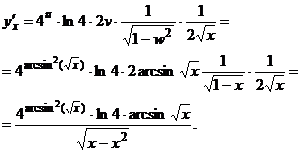
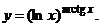 Вычислить
Вычислить 
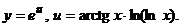
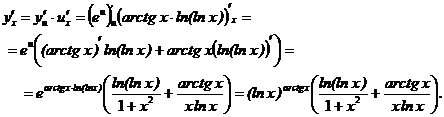

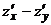 в точке
в точке 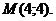
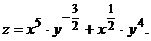
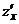 , считая у константой:
, считая у константой: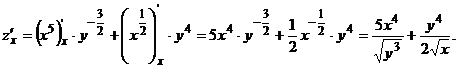
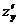 , считая х константой:
, считая х константой: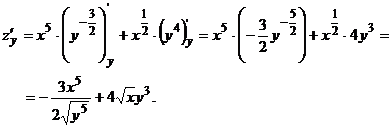
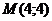 :
: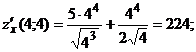
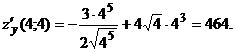
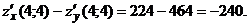
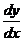 , если
, если 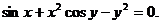
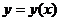 задана в неявном виде – уравнением
задана в неявном виде – уравнением 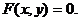 Воспользуемся формулой дифференцирования неявно заданной функции:
Воспользуемся формулой дифференцирования неявно заданной функции: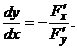


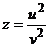 , где
, где 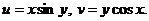 Найти
Найти 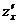 при
при 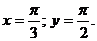
 где
где 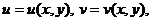 имеем
имеем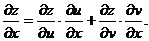
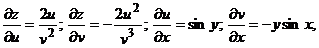
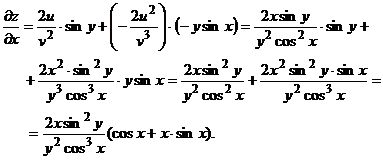
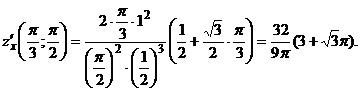
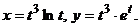
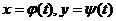 .
.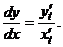

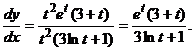

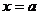 является вертикальной асимптотой кривой
является вертикальной асимптотой кривой  если
если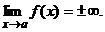
 является наклонной асимптотой кривой
является наклонной асимптотой кривой 
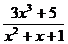 никогда не обращается в 0 (D=-3<0), значит, не существует точек, обращающих саму дробь в бесконечность, и вертикальных асимптот нет.
никогда не обращается в 0 (D=-3<0), значит, не существует точек, обращающих саму дробь в бесконечность, и вертикальных асимптот нет.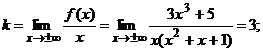
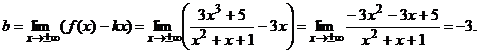
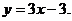
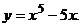
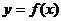 убывает, если
убывает, если 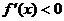 , и возрастает, если
, и возрастает, если 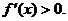 Найдем
Найдем 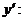
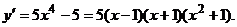
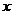
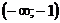
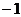
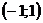
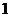
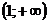
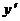
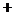
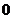

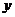
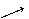

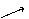
 .
.
 и вогнутой, если
и вогнутой, если  . Найдем
. Найдем 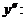
 ;
;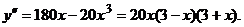
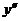 , а также промежутки выпуклости и вогнутости функции:
, а также промежутки выпуклости и вогнутости функции: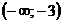
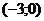
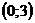
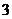
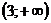
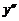


 +
+



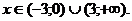

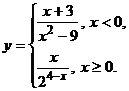
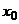 , если
, если 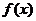 определена в некоторой окрестности этой точки и имеет в ней конечный предел, причем
определена в некоторой окрестности этой точки и имеет в ней конечный предел, причем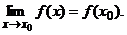
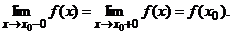
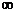 , то это разрыв II рода.
, то это разрыв II рода.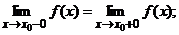

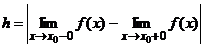 ).
).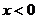 . Здесь
. Здесь 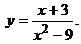 Функция не определена в точке
Функция не определена в точке 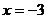 , значит, в этой точке разрыв.
, значит, в этой точке разрыв.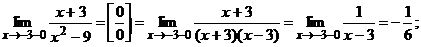
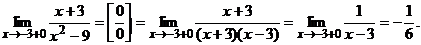
 значит, при
значит, при 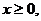 то
то 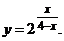 Функция не определена в точке
Функция не определена в точке 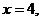 значит, это точка разрыва.
значит, это точка разрыва.
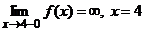 - точка разрыва II рода.
- точка разрыва II рода.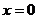 , так как при переходе через эту точку функция
, так как при переходе через эту точку функция 
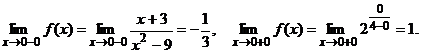
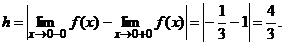
 разрыв I рода со скачком при
разрыв I рода со скачком при 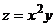 в точке М(2;1).
в точке М(2;1).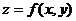 равна модулю градиента, а сам градиент – это вектор
равна модулю градиента, а сам градиент – это вектор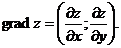
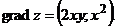
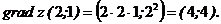
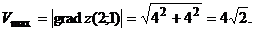
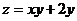 в точке М (1;-3) в направлении вектора
в точке М (1;-3) в направлении вектора 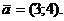
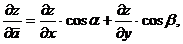
 - направляющие косинусы вектора
- направляющие косинусы вектора 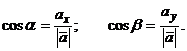
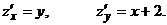

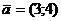 :
: